Восстановление параметров ионосферных возмущений по динамике серпообразных особенностей на ионограммах

Целью данной работы является исследование ионограмм, синтезированных при наличии в ионосфере возмущений различного типа, а также разработка метода решения обратной задачи определения параметров возмущений по ионограммам.

На дневных ионограммах вертикального и слабонаклонного зондирования часто наблюдается дополнительный след, имеющий серпообразную форму. Как правило, «серп» перемещается вниз, трансформируясь со временем в перегиб основного трека ионограммы [Дробжев, Яковец, 1977; Крашенинников, Лянной, 1991].

На рис. 1 показаны ионограммы с серпообразными особенностями, полученные 1 февраля 2010 г. с помощью ЛЧМ-ионозонда на короткой радиотрассе Усолье-Сибирское–Торы (дальность 130 км). Подобные ионограммы довольно часто можно наблюдать в утренние и вечерние часы зимнего сезона. На ионограммах видна эволюция «серпа». Периодичность снятия ионограмм на данной трассе составляет одну минуту, что позволяет проследить плавную динамику «серпа» от момента появления до исчезновения.

Установлено [Крашенинников, Лянной, 1991; Данилкин и др., 1987], что причиной появления серпообразных особенностей на ионограммах являются

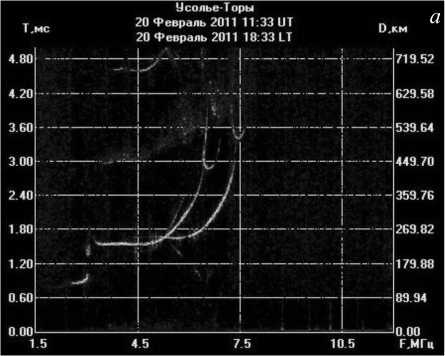
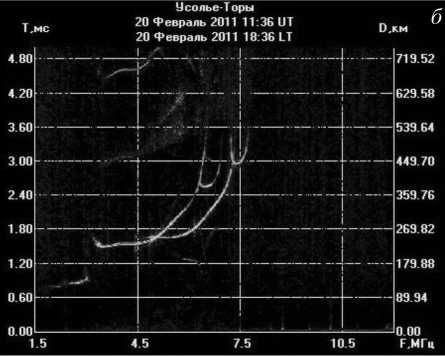
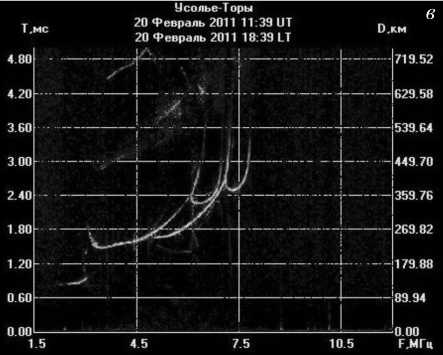
Рис . 1. Экспериментальные ионограммы радиотрассы Усолье - Сибирское – Торы .

перемещающиеся ионосферные возмущения, имеющие фронт, наклонный к горизонту. На рис. 2 показан типичный для зимнего времени профиль электронной концентрации, восстановленный методом Хуанга–Райниша [Reinisch, Huang, 1983], который используется в программном комплексе дигизонда DPS-4 [Reinisch et al., 1997], установленном в Иркутске в ИСЗФ СО РАН. Добавление к данному фоновому профилю положительного локализован-

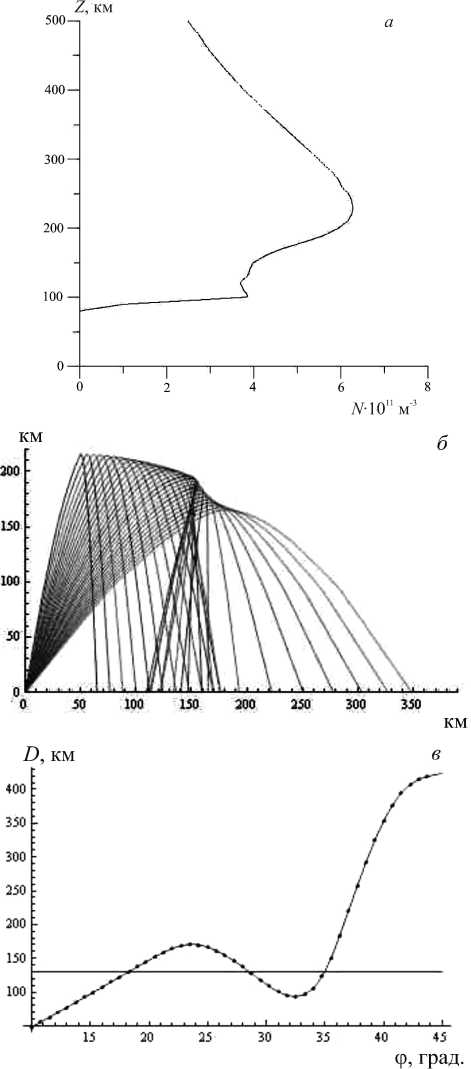
Рис . 2 . Фоновый профиль электронной концентрации ( а ) и соответствующие траектории радиоволн при нали чии возмущения ( б , в ).

ет для заданной рабочей частоты траектории лучей, отвечающих углам излучения из выбранного диапазона с фиксированным шагом (например, углам от 10° до 45° к горизонту с шагом 0.75° для рис. 2, б и в ). Полученный набор траекторий (рис. 2, б ) позволяет, используя сплайн-интерполяцию полиномами третьей степени, построить дальностно-угловую характеристику D (φ) (рис. 2, в ). Далее задача сводится к нахождению корней уравнения

D(φ)=D0, где D0 – дальность трассы, в нашем случае 130 км.

Было проведено моделирование ионограмм для различных видов возмущений. Результаты моделирования показывают, что по типу возникающих серпообразных особенностей возмущения можно условно разделить на три вида.

1. Мелкомасштабные локализованные воз мущения с масштабами порядка десятков кило метров

Такие возмущения образуют возвратные траектории, но практически не оказывают влияния на окрестность средней точки трассы, вследствие чего основной трек ионограммы остается почти без изменений. При этом сползание «серпа» на ионограмме в область меньших частот и меньших групповых задержек моделируется горизонтальным дрейфом возмущения в направлении источника излучения (на рисунках источник находится в начале координат). На рис. 3 приведены синтезированные ионограммы для возмущения гауссова типа

N ( x, z ) = N 0 ( z ) x

x 1 + 5 exp

^^^^B

^^^^

V

( ( х - х , )cos P~ ( z - z l )sin P)

^^^^

l x

( z - z l ) cos P + ( x - x l ) sin p l z

ного возмущения (увеличивающего концентрацию в области своей локализации) приводит к появлению «возвратных траекторий» (рис. 2, б ), т. е. траекторий лучей, отражающихся вдали от средней точки трассы, но приходящих на необходимую дальность 130 км. Именно такие траектории образуют «серп» на ионограмме.

Для моделирования была написана программа, реализующая алгоритм двумерной пристрелки лучей для синтеза ионограмм в приближении геометрической оптики. Входными параметрами программы являются профиль электронной концентрации, величина и наклонение магнитного поля, а также характеристики возмущения. Алгоритм рассчитыва-

cо следующими параметрами: интенсивность в центре возмущения составляет δ=25 % от фоновой электронной концентрации, угол наклона фронта возмущения к горизонтали β=0, пространственные масштабы l x = l z =20 км, высота центра z l =195 км, горизонтальная координата центра x l (отмечена на рис. 3) принимает последовательно значения 170, 160, 140 и 120 км. N 0 ( z ) – фоновая электронная концентрация, являющаяся функцией высоты.

2. Волнообразные возмущения

Накопленный экспериментальный материал показывает, что «серпы» чаще смещаются из области больших частот к малым. Однако для рассмотренного выше случая локализованных возмущений движение «серпа» может быть направлено равновероятно в обе стороны – так же как равновероятно направление горизонтального смещения возмущения. Однонаправленное движение «серпа» достаточно хорошо объясняется, например, механизмом распространения внутренних гравитационных волн. В связи с этим далее

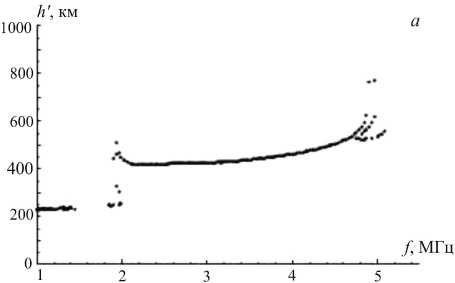
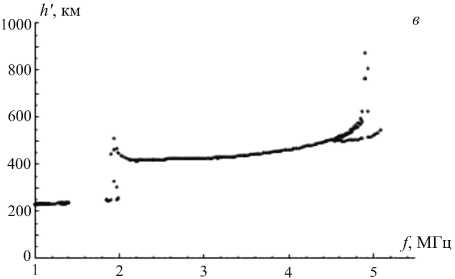
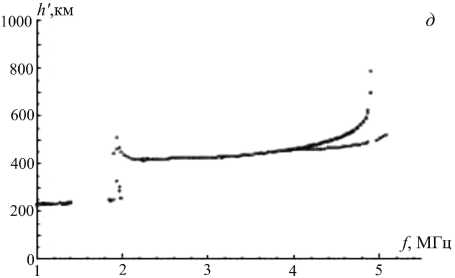
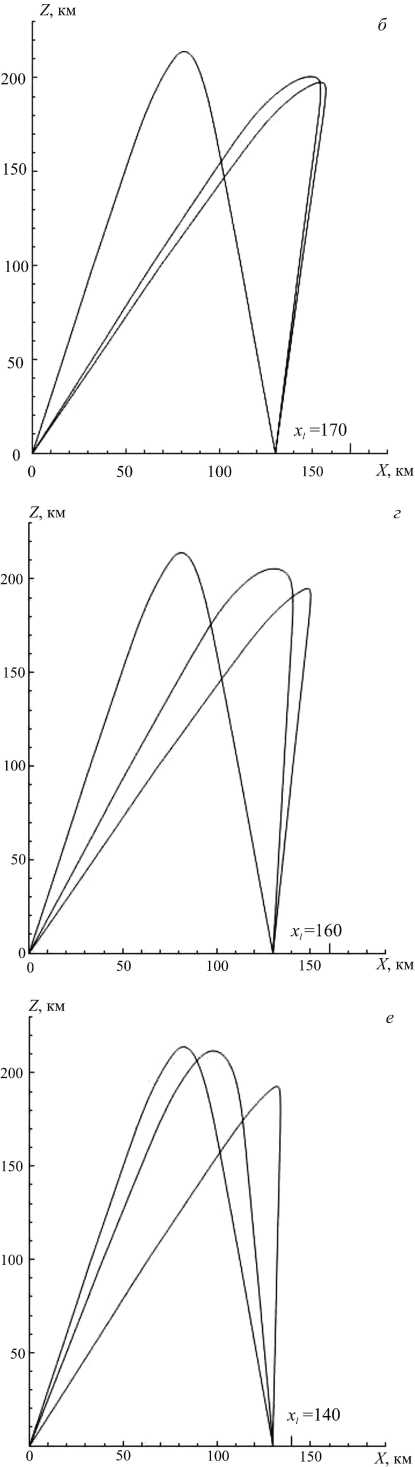
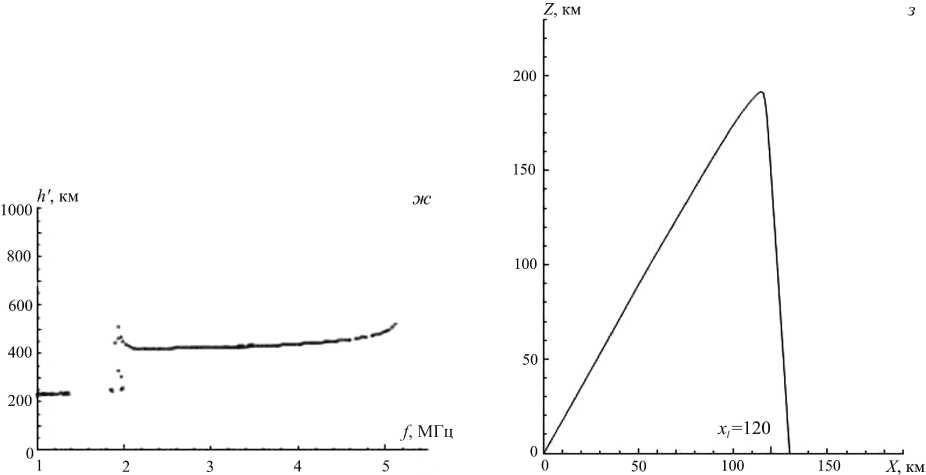
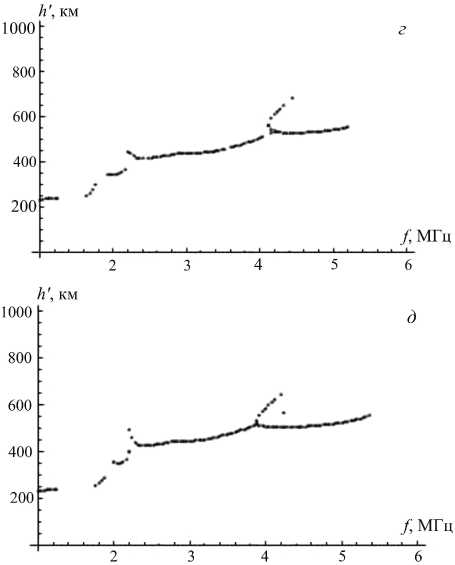
Рис . 3. Синтезированные ионограммы трассы Усолье - Сибирское – Торы ( а , в , д , ж ) и характерные траектории ( б , г , е , з ).

были рассмотрены волнообразные возмущения, задаваемые моделью [Вертоградов и др., 2005]

N ( z , x , t ) = N ₀( z ) x

2 n

x (1 + 8 cos( k z + k x--t + Ф 0 )) , zx _T

где k z =(2π/Λ)cosγ, k x =(2π/Λ)sinγ – волновой вектор ПИВ с длиной волны Λ, T – период ПИВ; Φ 0 – начальная фаза; угол γ задает направление фазовой скорости возмущения.

В рамках данной модели были синтезированы ионограммы для различных наборов параметров γ, Λ, Tt . На рис . 4 приведены характерные для модели волнообразных возмущений ионограммы для δ=30 %, Λ=100 км, γ= –30° и последовательных моментов времени t _ 10 11 12 13 14 15 16 17

T ” 15^, 15^,15^,15^,15^,15^,15^,15.

Следует отметить, что в рамках данной модели получаемые ионограммы имеют вид «рюмки». В эксперименте в ряде случаев можно наблюдать ионограммы такого вида. Однако в большинстве случаев серпообразные особенности имеют вид, показанный на рис. 1, и модель волнообразных возмущений для их описания не всегда приемлема.

значения от 210 до 170 км с шагом 10 км. На рис . 6 даны соответствующие картины изолиний для z l =210, 190 и 170 км. Рассмотрен второй тип профиля электронной концентрации, используемый в ИСЗФ СО РАН, –

• 3.    Возмущения типа « наклонный слой »

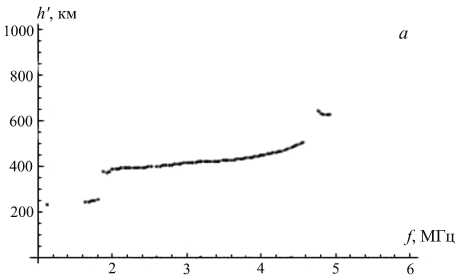
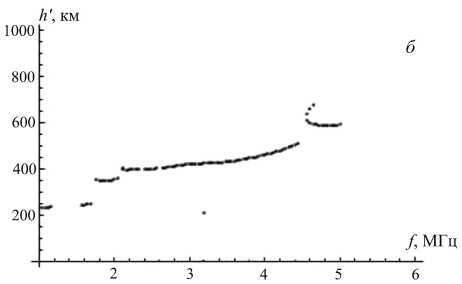
Была рассмотрена модель возмущения электронной плотности в виде наклонного слоя. Интенсивность этого возмущения в направлении, перпендикулярном фронту, спадает по гауссову закону (1). В направлении вдоль фронта интенсивность возмущения меняется слабо или не меняется вообще, т. е. выполняется условие соответственно l x >> l z или l x =∞ . На рис. 5, б – е показаны типичные для такой модели ионограммы для значений параметров β=40°, l x =100 км, l z =10 км, x l =150 км, z l принимает

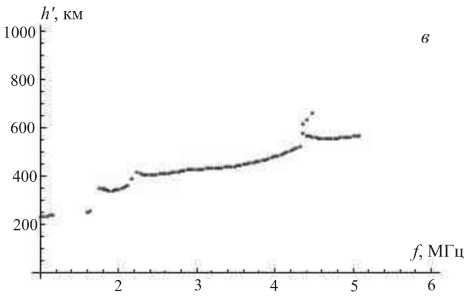
полученный с помощью модели IRI-2000 (рис . 5, а ). Принципиальным отличием от рассмотренного выше случая является то , что основной трек ионограммы здесь смещается под воздействием возмущения, а его высокочастотная часть может исчезать, когда возмущение, опускаясь , начинает изменять электронную концентрацию в средней точке трассы .

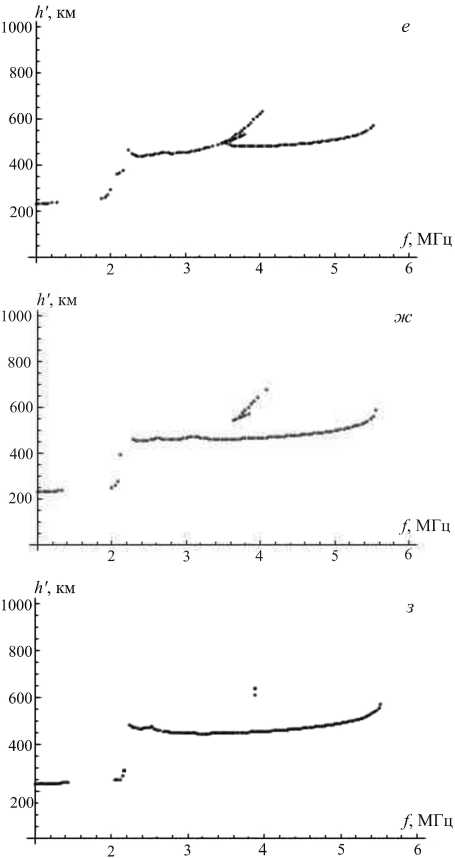
Рис . 4. Синтезированные ионограммы трассы Усо - лье - Сибирское – Торы для модели волнообразных возму щений .

• 4.    Определение угла наклона и оценка скоро сти дрейфа возмущения

Модель наклонного слоя является достаточно простой для анализа, в отличие от модели волнообразных возмущений; при этом синтезированные ионограммы в ряде случаев получаются визуально наиболее близкими к наблюдаемым при эксперименте. Для описания методики восстановления параметров возмущения будем вначале использовать в качестве примера ионограммы на рис. 5, так как изначально известные параметры возмущения дают возможность проверить корректность решения.

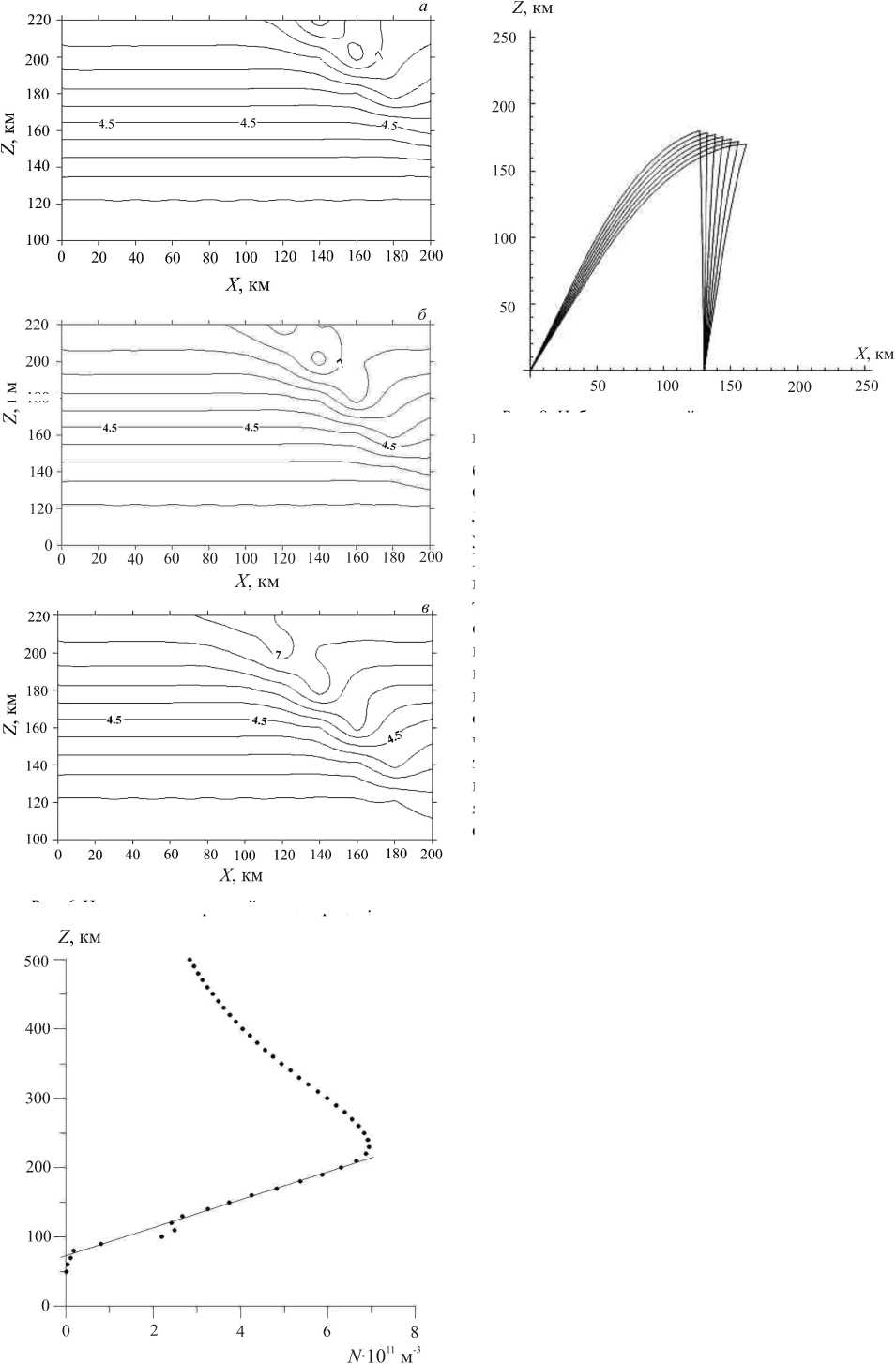
Вид возвратных траекторий, составляющих серп на ионограмме, дает основание принять, что лучи отражаются от зеркальной плоскости, наклон которой совпадает с наклоном возмущения. Кроме того, профиль электронной концентрации до высот отражения аппроксимируется линейной моделью начиная с некоторой высоты z n , ниже которой электронная плотность пренебрежимо мала (рис. 7), – в этом случае можно получить траектории лучей в аналитическом виде. Далее будет показана правомерность данных приближений.

С помощью метода наименьших квадратов получены наклон линейного слоя и высота «начала» ионосферы:

— = 5 - 10 6 м " 4 , z = 74.7 км.

A z

Траектория луча в линейном слое ионосферной плазмы задается уравнением z (x) = " x2------2— + x - Ctgф n,

4L sin фn где   φn   – начальный угол   излучения,

4 n ² £₀ mf ² ( A N y¹

L =----0           , £0 — диэлектрическая прони- e2    V Az )

цаемость, m и e – масса и заряд электрона, f – частота зондирования.

Обозначим φ m – угол прихода луча, x n – смещение луча по горизонтали до точки отражения при распространении выше z n , x m – смещение после отражения, x 0 , z 0 – координаты точки отражения. Поставим условие, чтобы траектории сходились в одной точке:

Z n ^ф n ⁺ x n = D 0 ⁺ Z n ^tg ф m ⁺ x m ,                ⁽³⁾

2 x_n

4 L sin² ф _n

⁺ x n с1д ф n

x

" 77-^ ⁺ x m CtgW m .

⁴ L sin ф

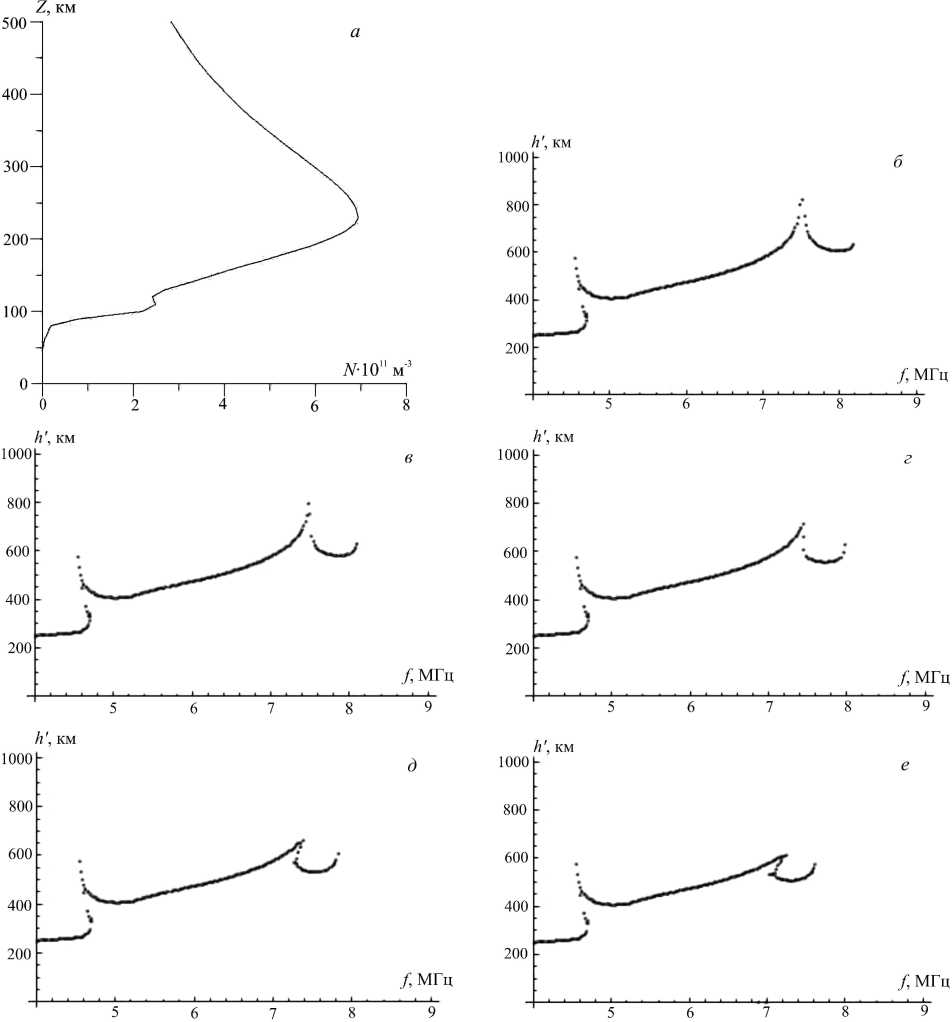
Рис . 5. Профиль электронной концентрации по модели IRI ( а ), ионограммы , синтезированные для модели наклонно го слоя ( б – е ).

Теперь выберем на ионограмме точку ( f 0 , h '₀ ) , соответствующую минимуму «серпа» (по действующей высоте). Например, для графика 5, г это точка (7.72 МГц, 557 км). Потребуем, чтобы суммарный групповой путь на данной частоте был фиксирован :

zn    |    zn+ xn    |   xm cos фn  coS фm  sin фn  Sin фm

= h '0 .

Система уравнений (3)–(5) определяет связь между четырьмя неизвестными x n , x m , φ n , φ m . Неоднозначность приводит к тому, что каждому начальному углу φ n соответствует своя траектория, удовлетворяющая условиям (3)–(5) (рис. 8).

Отметим, что в соответствии с законом отражения от зеркальной поверхности биссектриса угла между касательными в точке отражения к обоим участкам траекторий (рис. 9) будет совпадать с нормалью к фронту возмущения.

Для разрешения неоднозначности введем естественное условие, согласно которому будем полагать, что возмущение, вызывающее «серп» на ионограмме, движется с неизменным углом наклона, т. е. в нашем приближении зеркало опускается параллельно самому себе. Для этого необходимо рассмотреть ионограмму на рис. 5, д (которая гипотетически снята в последующий момент времени, скажем, через одну или две минуты после ионограммы на рис. 5, г ). Для нее будет другая точка минимума «серпа» – ( f 02 , h 'o 2 ) =(7.52 МГц, 532 км), а также другой набор неизвестных x n 2 , x m 2 , φ n 2 , φ m 2 . Биссектрисы углов между касательными к траекториям в точках отражения

^ 180 -

+ arcctg

^{+ Ct} g ф m 1

2 L sin ^ф n 2

+ arcctg

⁺ ^ m 2

+ arcctg

⁺ x n 1^Ct g Ф n 1 =

⁴ L 1 ^si n ² Ф n 1

где α – угол наклона возмущения к горизонту.

Условия равномерного движения зеркала:

Рис . 8. Набор траекторий радиоволны , удовлетворяю щих условиям (3)–(5).

⁺ c ^t g ф n 2 I ⁺

2 x_{n 1}

x n2

x _n m 2

x_{m 1}

X 2

m 3

^-ct g ^a ( x n 1 ⁺ Z n ^t g Ф n 1 ) ⁺ Z a ,

I

^{+ Ct} g Ф m 3 , J

--:--------

² L 1^Sin Ф m 1

^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

² L 2^Sin2 Ф m 2

² L ^Sin ² Ф m 3

7 — n

= arcctg I -

I x                           I

= arcctg I ^-       .^{n 3} ----+ c ^t g ф n з I +

( ² L 3 sin ф n 3          J

I x                          I

2 a = arcctg-- n ¹:--- + ctg ф +

( 2 L , sin ² ф n 1    “'"J

Рис . 6 . Изолинии электронной концентрации .

будут в обоих случаях (см. 5, г и д ) сонаправлены. Однако нетрудно увидеть, что введение этого условия не снимает неоднозначности, так как на семь уравнений теперь приходятся восемь неизвестных. Последнее вполне естественное условие, которое необходимо ввести для однозначного определения точек отражения (следовательно, угла наклона фронта возмущения и скорости его дрейфа), заключается в том, что возмущение движется равномерно в интервале между тремя последовательно полученными ионограммами. Например, будем считать, что три ионограммы на рис. 5, г , д , е получены через равные интервалы времени (так же как экспериментальные ионограммы на рис. 1) и в это время зеркальная поверхность двигалась с постоянной скоростью. Таким образом, имеем условие сонаправленности биссектрис

Рис . 7. Аппроксимация профиля IRI линейной моделью .

z

n

^^^^в

2 x_{n 2}

⁴ L sin² Ф n 2

⁺ x n 2 ^Ctg Ф n 2

= - Ctg a ( x n 2 + Z n tg f n 2 ) ⁺ Z a ^{- A} ,

z

x_{n 3}

⁴ L sin² Ф n 3

⁺ x n 3 ^Ctg 9 n 3 =

= ^{- c}tg ^a ( x n 3 ⁺ Z n ^tg ф n 3 ) ⁺ Z a ^- 2 ^ Z .

Здесь Δ z – смещение по высоте отражающего слоя между моментами снятия второй и первой ионограмм, а также третьей и второй.

Таким образом, в поставленной задаче входными

AN параметрами являются наклон линейного слоя , Az

«начало» ионосферы zn, точки минимума на «серпах» последовательно снятых с равным временным интервалом ионограмм (foi, h '01), (f02, h '02), (f03, h 03) • Данная задача была решена численно следующим образом. Вначале определялись зависимости угла наклона биссектрисы α от начального угла излучения φni для каждого из трех случаев i=1, 2, 3. Очевидно (рис. 8), что функции αi(φni), а следовательно, и обратные функции φni(α) являются однозначными и монотонными. Каждому начальному углу φn соответствует единственная траектория, поэтому далее нетрудно получить однозначные функции xni(α). Теперь система (7) приводится к виду z0i (a) = -ctga • x0i (a) + Za - iAZ, i=1, 2, 3,                                              (8)

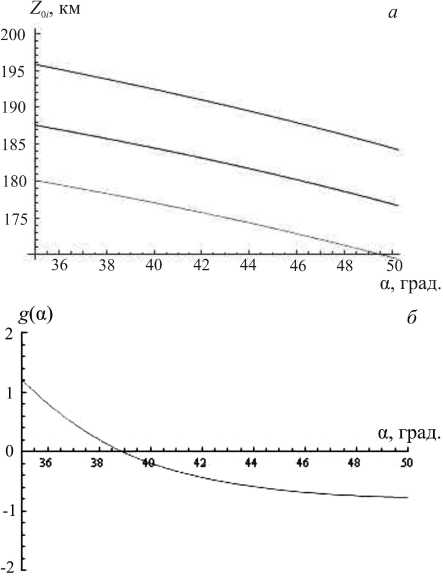
Рис . 10. Определение параметров возмущения .

где x_0{ ( a ) , z ₀ i ( a ) - точки отражения траекторий (см. рис. 8).

Система уравнений (8) сводится к уравнению, определяющему искомый угол α:

g ^(a) = ^z oi ^{(a) + 2 z} 02 ^{(a)   z} 03 ^{(a) +}

+ctga(- x01 (a) + 2 x01 (a)- x03 (a)) = 0.

На рис. 10 показаны функции z ₀ i ( a ) ( а ), а также решение уравнения (9) ( б ).

На рис. 11, г показаны полученные в результате

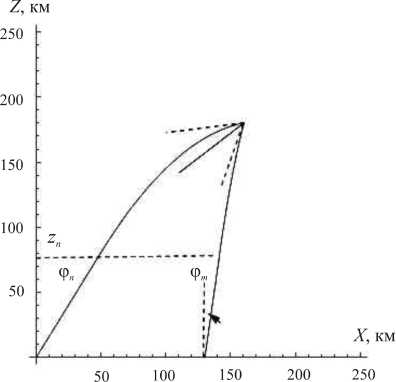
Рис . 9. Траектории луча в линейном слое ионосферы .

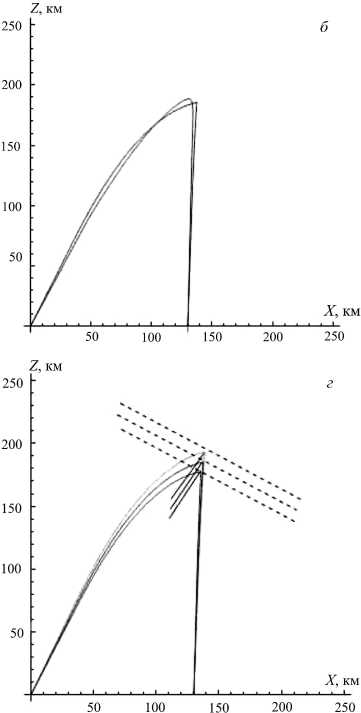
решения траектории. На графиках на рис. 11, а , б , в даны траектории лучей, полученные в результате численного решения системы лучевых уравнений с последующей пристрелкой с использованием оригинального профиля на рис. 5, а (им соответствуют ионограммы на рис. 5, г , д , е ). Показаны также траектории, полученные в описанном выше приближении «линейный слой – падающее зеркало». Можно видеть достаточно хорошее совпадение точных и приближенных траекторий. Например, на рис. 11, б для точной траектории углы излучения и прихода φ n =28.5°, φ m =1.3°, тогда как для приближенной траектории φ n =26.7°, φ m =1.9°. Погрешность такого же порядка имеет место и для рис. 11, а , в .

Итак, в результате решения были получены два основных параметра – α=38.9°, Δ z =7.1 км. Видно, что угол наклона возмущения в данном приближении определяется достаточно точно (изначально моделирование ионограмм проводилось для α=40°), тогда как смещение возмущения (или скорость его дрейфа) – со значительной погрешностью. Вероятно, это связано с тем, что угол падения радиоволны на возмущение приближенно равен углу выхода и, несмотря на то, что поворот луча внутри возмущения происходит постепенно, возмущение можно рассматривать как «черный ящик», имеющий свойства, подобные свойствам зеркальной поверхности. При определении скорости дрейфа возмущения данная методика дает погрешность, видимо, в связи с тем, что для различных рабочих частот «глубина проникновения» радиоволны в возмущение разная и для увеличения точности следует вводить некоторый «фактор проникновения», являющийся функцией частоты.

Наконец, поясним смысл введения приближения линейного слоя . Ясно, что данную методику можно реализовать, численно решая систему лучевых урав-

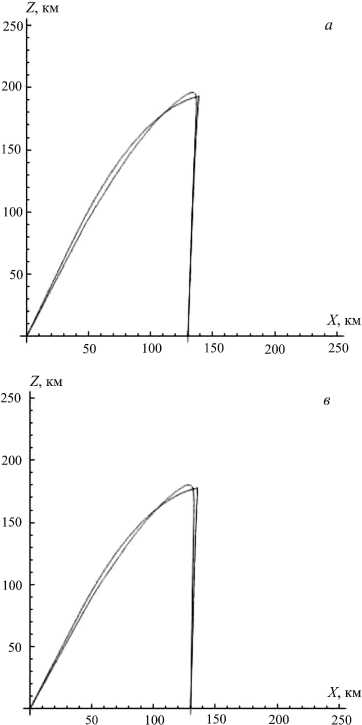
Рис . 11. Сравнение точных траекторий ( в приближении геометрической оптики ) и траекторий в приближении « на клонного зеркала » ( а , б , в ); траектории , полученные в результате решения уравнения (9) ( г ).

нений для произвольно заданного профиля электронной концентрации, так же как это делается при синтезе ионограмм . Однако при этом моделирование одной ионограммы при приемлемом разрешении по частоте и точности пристрелки занимает несколько часов . В таких условиях будет затруднена интерпретация ионограмм в режиме реального времени (в промежутках между снятиями ионограмм, составляющих 1 мин). Поэтому возникает необходимость применять, например , приближение линейного слоя, позволяющее записывать траектории лучей в аналитическом виде, что приводит к сокращению времени расчета и делает применимой данную методику для экспресс-анализа. Кроме того , моделирование показывает, что приближение линейного слоя вносит меньшую погрешность по сравнению с погрешностью модели «зеркала», на которой основана описанная методика.

Заключение

В работе было проведено моделирование ионограмм в условиях возмущенной ионосферы для двух типов профилей, используемых в ИСЗФ СО РАН, – для профиля, восстановленного с помощью цифрового ионозонда DPS-4, и профиля, полученного с помощью модели IRI-2000. Проведенное моделирование подтверждает, что движение «серпа» на ионограмме является результатом движения возмущений в ионосфере. Описанный в работе метод позволяет определять такие параметры перемещающихся ионосферных возмуще- ний, как наклон фронта и скорость дрейфа, по трем ионограммам с серпообразными особенностями, снятым через равные интервалы времени.

Работа выполнена при поддержке гранта РФФИ № 11-05-00892-а.