Возбуждение релаксационных колебаний на искривленной межфазной границе в условиях внутренней задачи

Исследование процессов массообмена на границе двух несмешиваемых жидких многокомпонентных растворов — задача актуальная и сложная. Здесь задействован целый ряд физических явлений, включающий: процессы адсорбции/десорбции поверхностно-активных веществ (ПАВ); всевозможные фазовые переходы как на межфазной границе (образование монослоя [1] ), так и вблизи нее (например, самопроизвольную ассоциацию молекул ПАВ в растворе — мицеллообразование [2] ); процессы диффузии компонентов, которые могут зависеть как от концентрации рассматриваемого компонента (концентрационно-зависимая диффузия [3] ), так и учитывать влияние других компонентов (кросс-диффузия [4] ); массоперенос благодаря концентрационной конвекции Марангони [5] , возникающей вследствие неоднородности распределения ПАВ на границе жидкостей; концентрационную конвекцию Релея–Бенара в объеме жидкостей, если имеется поле силы тяжести или другое инерционное поле. В случае неизотермических условий ко всему выше перечисленному может добавиться еще и термокапиллярная неустойчивость Марангони, отягощенная эффектами термоконцентрационной конвекции [6] . Сочетание или конкуренция этих механизмов приводят к развитию колебательных конвективных режимов. Их исследованию посвящено значительное число работ, имеющих преимущественно экспериментальный характер (см. свежий обзор по данной тематике [5] ).

Анализ публикаций показывает, что хорошо изучены осциллирующие течения вблизи неподвижных пузырьков и капель в стратифицированных растворах ПАВ [6–10]. Вероятно, впервые релаксационные колебания наблюдались вблизи поверхности горизонтального воздушного пузыря, окруженного водным раствором одного из ПАВ (использовались уксусная кислота и набор спиртов) [7]. Позднее эффект воспроизведен этими же авторами вблизи поверхности жидкость–жидкость, но также в условиях внешней задачи изучалось поведение капли хлорбензола, окруженного водным раствором изопропанола [8]. Обсуждение первых работ по данной тематике приводится в обзоре [9]. В работе других авторов эффект независимо «переоткрыт» в [10], где изучалось поведение капелек парафинового масла в окружающем водном растворе 2-пропанола. Приложение релаксационных колебаний вокруг пузыря или капли для перемешивания ингредиентов в микрожидкостном реакторе проточного типа рассмотрены в [11]. Во всех процитированных выше работах вокруг включения создавалась стратификация растворенного ПАВ, которая стимулировала возникновение концентрационной конвекции Марангони. Короткая вспышка интенсивного массопереноса вблизи поверхности приводила к локальному исчезновению градиента ПАВ и прекращению конвекции. Показано, что для зарождения периодических колебаний требуется возвратный механизм, которым может служить, например, поле силы тяжести. Через некоторое время после затухания конвекции раствор ПАВ вновь стратифицировался, система приходила в исходное состояние. Кроме того, исследования показали, что для наблюдения колебаний требуется ПАВ, молекулы которого подчиняются диффузионной кинетике. В этом случае характерное время диффузии ПАВ много больше времени его адсорбции. Молекулы с длинной гидрофобной частью, которые подчиняются барьерной кинетике, поглощаются межфазной поверхностью и формируют монослой, препятствующий развитию конвекции Марангони.

Математические модели релаксационных колебаний в условиях внешней задачи представлены в работах [12 –14] . Во всех случаях, скрыто или явно, предполагался эффект запаздывания в срабатывании конвекции Марангони. Например, в работах [13, 14] авторы ввели в модель феноменологическое предположение о специальных реологических свойствах межфазной поверхности, которые требовали достижения определенного порога силового воздействия на границу для начала ее движения. Это требование отсутствует в работе [12] , однако, постановка задачи все равно неявно имела своим условием запаздывание: источник ПАВ находился на некоторой глубине от поверхности, что приводило к задержке выхода молекул ПАВ на поверхность. Следует отметить, что межфазная граница в [12 –14] считалась плоской.

Недавно экспериментально обнаружен новый вариант колебательного режима концентрационной конвекции Марангони, которая возбуждается в условиях внутренней задачи [15] , то есть внутри капли, зажатой между широкими пластинами и имеющей форму сплющенного цилиндра. Этот режим связан с абсорбцией ПАВ из однородного внешнего раствора в каплю и последующим формированием в ней устойчивой вертикальной стратификации среды по плотности и, соответственно, появлением перепада концентрации вдоль боковой поверхности капли. В эксперименте капля из дистиллированной воды помещалась в органический раствор на основе хлорбензола, бензола и уксусной кислоты. Начальная концентрация кислоты в тройной смеси варьировалась от 0.25 до 2.0 моль/л. В ходе опытов концентрация кислоты в капле воды изменялась от 0 до 8 моль/л, то есть накапливалась там в большей концентрации, чем в исходном растворе. Релаксационные колебания в этом случае генерировались прежде всего внутри капли.

Настоящая работа преследует несколько целей:

– применяется математическая модель, предложенная в [13, 14] , но в приложении к внутренней задаче;

– процессы массопереноса рассматриваются как внутри, так и вокруг капли, следовательно, межфазная граница искривлена, что существенно влияет, как показано в [10] , на вид релаксационных колебаний;

– исследование проводится в режиме компьютерной симуляции, которая приближена к условиям эксперимента, что подразумевает использование уравнений в размерном виде и задание максимально реалистичных значений физических величин.

Моделирование выполнено с помощью пакета COMSOL Multiphysics. Численные результаты сравниваются с данными эксперимента [15] .

• 2.    Постановка задачи

  • 2.1.    Математическая модель

В эксперименте [15] прямоугольная кювета с раствором ПАВ имела размеры 90 х 25 х 1.2 мм, что означает сильное сжатие по одному из горизонтальных направлений. При этом зажатая между широкими вертикальными пластинами кюветы капля воды приобретала форму сплющенного цилиндра, радиус которого более чем на порядок превышал узкий зазор в кювете. Положение капли стабилизировалось с помощью методики «гидроневесомости» [14 –16] , согласно которой в ПАВ создается вертикальный градиент плотности, и капля сама находит положение равной плотности. Поле плотности внешней по отношению к капле среды подбиралось с помощью смешения разных количеств бензола и хлорбензола. Дополнительную стабилизацию капли обеспечивали капиллярные эффекты вблизи межфазной поверхности, натянутой между широкими пластинами ячейки.

При натурных испытаниях заметные деформации поверхности капли не наблюдаются на любых этапах развития массопереноса в системе. Кроме того, априорные оценки показывают, что характерный размер конвективных вихрей также существенно превышает величину зазора между каплей и стенкой кюветы; это позволяет использовать для исследования приближение Хеле-Шоу с переходом к двумерной постановке задачи.

Таким образом, будем рассматривать прямоугольную область размерами 90 x 40 мм, которая заполнена органической смесью бензола и хлорбензола с растворенной в ней уксусной кислотой. Концентрация раствора ПАВ не превышает 2 моль/л. В центре области находится неподвижная капля диаметром 6 мм, которая в начальный момент времени состоит из чистой воды. Предполагается, что форма капли фиксированная, и капля неподвижна. Каплю и окружающую ее область считаем двумя фиксированными доменами, в каждом из которых зададим уравнения конвекции и диффузии растворов, а на границе доменов (на межфазной поверхности) учтем соответствующие граничные условия. Физические процессы в данной задаче предполагают адсорбцию уксусной кислоты поверхностью капли и последующую десорбцию молекул кислоты в обе стороны от межфазной поверхности. Последнее приводит к проникновению кислоты в каплю и образованию водного раствора кислоты. Физические свойства жидкостей, заполняющих домены, представлены в таблице. Сведения о свойствах растворов уксусной кислоты в воде и бензоле взяты из источников, которые указаны. Здесь mf 1 — массовая доля уксусной кислоты в водном растворе. Некоторые характеристики растворов зависят от концентрации. Так, зависимость плотности раствора от концентрации становится причиной различной плавучести у элементов системы. Это может вызвать развитие конвекции в жидкостях вблизи поверхности капли, на которой происходит массообменный диффузионный процесс. Зависимость коэффициента поверхностного натяжения от концентрации стимулирует зарождение концентрационно-капиллярной конвекции Марангони на поверхности капли. Учитывается также взаимосвязь вязкости и концентрации. Поскольку в задаче рассматриваются слабые растворы уксусной кислоты, все характеристики растворов зависят от своей концентрации линейным образом.

Таблица. Свойства системы вода/органическая смесь (50% бензола и 50% хлорбензола) с межфазным массопереносом уксусной кислоты; индекс 1 соответствует водной фазе, индекс 2 – органической фазе

Физическая величина	Обозначение	Размерность	Значение	Источник
Молярная масса воды	µ 1	г/моль	18	[17]
Молярная масса органической смеси	µ 2	г/моль	95	[17]
Плотность воды	ρ 01	кг/м 3	998	[15]
Плотность водного раствора кислоты	ρ 1	кг/м 3	p oi +0 . 00834 [кг/моль] • C 1	[18]
Плотность органической смеси	ρ 02	кг/м 3	1048	[15]
Плотность органического раствора кислоты	ρ 2	кг/м 3	Р 02 — 0 . 001 97 [кг/мольр С 2	[18]
Динамическая вязкость водного раствора кислоты	η 1	Па ^ с	(1 . 0+2 . 1 - mf i ) - 10 - 3	[18]
Динамическая вязкость органического раствора кислоты	η 21	Па ^ с	0 . 74 • IO - 3	[17]
Коэффициент диффузии кислоты в воде	D 1	м 2 /с	10 - 9	[17]
Коэффициент диффузии кислоты в органическом растворе	D 2	м 2 /с	10 - 9	[17]
Поверхностное натяжение на границе вода/бензол	σ 0	Н/м	0.035	[18]
Поверхностное натяжение на границе вода/бензол с кислотой	σ	Н/м	0 . 0343+0 . 174 mf 1	[18]
Коэффициент разделения кислоты на границе вода/смесь	k µ	б/р	7	[19]
Коэффициент массопереноса кислоты на границе вода/смесь	k c	м/с	10 6 : 10'	[15]
Начальная концентрация кислоты в органической смеси	c 0	моль/л	0.5 ^ 2	[15]
Толщина ячейки Хеле-Шоу	d	мм	1.2	[15]

Сформулируем математическую модель протекающих процессов. Предполагаем, что течение в объеме капли и в области является ламинарным и описывается, соответственно, уравнениями Навье–Стокса в приближениях Буссинеска [20] и Хеле-Шоу [21] и уравнением неразрывности:

ρ 0 i

d U i    6.

~аТ '    ^{u ; |}

-V p i +п i V 2 U i - 3n i U i +P i g ,

V- U i = 0,

где индекс i принимает значения 1 (для водной капли) и 2 (для внешней среды — органического раствора), t — время, ρ 0 i — плотность растворителя, g — вектор ускорения свободного падения, u i , p i — скорость и давление жидкости, V — оператор набла, j i , s i — коэффициент динамической вязкости и плотность раствора.

Уравнения переноса уксусной кислоты в фазах имеют следующий вид:

∂c

-^ + ( U i •V )c _! = D iV² с _г ,                                       (3)

где c i — концентрация и D i — коэффициент диффузии кислоты в соответствующей фазе.

Данные эксперимента [15] свидетельствуют о том, что кислота поглощается каплей воды из окружающего раствора. При этом, из-за эффекта контракции (уменьшения первоначального объема вследствие сжатия), молекулы уксусной кислоты проявляют себя в водной и органической фазах по-разному. По отношению к смеси бензола и хлорбензола кислота выступает как легкая примесь (отрицательная контракция). Растворение уксусной кислоты в воде сопровождается положительной контракцией, из чего следует, что кислоту следует рассматривать здесь как тяжелую примесь. Под действием силы тяжести в капле начинается процесс стратификации водного раствора кислоты: внизу капли он имеет большую концентрацию. Снаружи капли раствор расслаивается значительно слабее вследствие сглаживания за счет диффузии и небольшой объемной конвекции. Таким образом, в части капли, примыкающей к межфазной границе, складываются условия для возникновения конвекции Марангони. Поэтому коэффициент поверхностного натяжения вычисляется по объемной концентрации водного раствора уксусной кислоты вблизи внутренней боковой поверхности капли по формуле [18] :

a = 0.0343 - 0.174 mf 1 Н/м,                                      (4)

Пакет COMSOL Multiphysics предлагает соответствующую модель для расчета конвекции Марангони, имеющей место, когда поверхностное натяжение на границе жидкостей зависит от концентрации растворов или распределения температуры. Ее вклад в движение жидкости осуществляется через динамическое условие баланса напряжений, возникающих на межфазной поверхности [22] :

—pI+n ( Vu+VT• n(Vu)T — | (V-u)I n = a(VT •n)n—VT a,

где индекс τ обозначает тангенциальное к границе направление, в скобки [...] заключена разность величин на разрыве. В уравнении (5) слева стоит разность тензоров вязких напряжений, заданных в средах 1 и 2, в правой части записаны слагаемые, связанные с поверхностным натяжением; первое слагаемое включает среднюю кривизну поверхности, а второе можно рассматривать как напряжение Марангони, возникающее из-за вариаций коэффициента поверхностного натяжения вдоль поверхности капли.

При постановке граничных условий для концентраций растворов уксусной кислоты в окрестности капли и в капле следует учитывать различие соответствующих химических потенциалов в бензоле–хлорбензоле и воде. Известно, что на границе двух жидкостей поток частиц вещества J пропорционален концентрации и градиенту химического потенциала µ:

J ~^— c ^(V n ripT ,

µ ≡

∂G

^∂N p,T

где G — энергия Гиббса, N — число частиц в системе. Следует отметить, что химический потенциал раствора зависит от его концентрации:

c i

^ = ^(T )+RT In — , ci0

где ^_i0 — стандартный химический потенциал при концентрации растворенного вещества c _{i 0} =1 моль/л. Он зависит от растворяемого вещества и растворителя. Стандартные химические потенциалы уксусной кислоты в воде и в бензоле заметно отличаются. Условие равновесия, при котором прекращается массообмен капли с окружающей средой, может быть получено из (6) и (7) следующим образом:

- ^20

c l    ^k ^ ^c 2 , k ^   ~

µ 10

Д _г о = exp

№о 1

RT .

После достижения системой состояния равновесия, концентрация кислоты в капле будет выше в k _µ раз, то есть капля воды в этой задаче выступает как аккумулятор кислоты. Этот множитель называется коэффициентом разделения (см. Табл.).

В математической модели ключевым предположением является гипотеза о специальных реологических свойствах межфазной границы. В работах [13, 14] считалось, что эта поверхность имеет неньютоновский характер

( a )

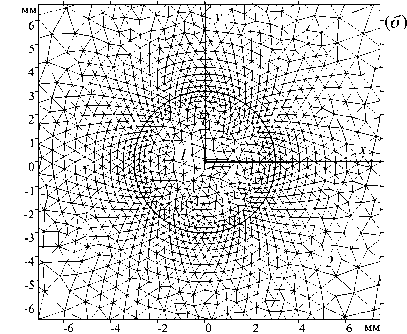
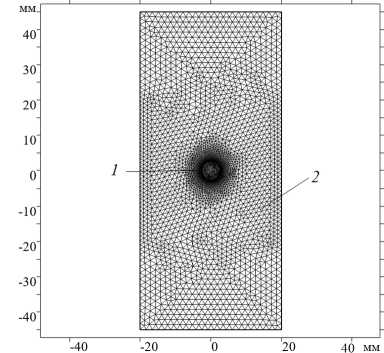
Рис. 1. Расчетная сетка для всей расчетной области ( а ) и в увеличенном размере вблизи капли ( б ); цифрами 1 и 2 обозначены расчетные подобласти капли и внешней среды

поведения. Это означает, что она приходит в движение только после того, как внешнее усилие, приложенное к ней, превысит некоторое значение. Следуя этому, допускаем, что на поверхности капли существует такая реология ПАВ, что напряжение f M , возникающее благодаря концентрационному эффекту Марангони, вычисляется по формуле:

f M = -H (|V t <7 |- f o ) V _T a,                                    (9)

где H(x) — функция Хэвисайда, f o — порог возникновения концентрационно-капиллярной конвекции. Таким образом, вязкие напряжения на поверхности капли, появляющиеся вследствие эффекта Марангони, учитываются только в те моменты времени и на той части поверхности, где они превышают пороговое значение. Если напряжение (9) не достигло порогового значения, поверхность остается неподвижной.

Граничные условия задачи сформулируем следующим образом:

Л: U i =0, - nJ = 0,                                    (10)

Г : U in = 0, U 1 T = U 2t , n ^ J 1 = - nJ 2 = k c (c 2 — k^l ),                      (11)

где Λ и Γ обозначают, соответственно, внешнюю границу ячейки Хеле-Шоу и межфазную границу. Как видно из (10) , на стенках области скорость жидкости равна нулю и отсутствует поток уксусной кислоты через твердые стенки. На поверхности капли (11) нормальная компонента скорости нулевая, а тангенциальная компонента непрерывна. Граничные условия транспорта (диффузии) кислоты через поверхность капли представлены равенством потоков и условием равновесия фаз, где k c — коэффициент массопереноса кислоты на границе вода/органическая смесь.

Начальные условия задачи имеют вид:

t = 0: U 1 =0, U 2 = 0, C l = 0, C 2 = C o ,                               (12)

где c ₀ — начальная концентрация уксусной кислоты в органической фазе.

• 2.2.    Численная реализация модели

Для решения краевой задачи (1) - (12) применялся пакет COMSOL Multiphysics. Расчетная область разбивалась на элементы с помощью триангулярной сетки со сгущением вблизи поверхности капли (Рис. 1) . В численной модели использовалась декартова система координат с началом в центре капли (Рис. 1б ), а в качестве вспомогательной — полярная система координат, радиус и полярный угол которой определялись как r² = x ² +y ² , x = гсов(ф - 90 ° ), у = Г8ш(ф — 90 ° ).

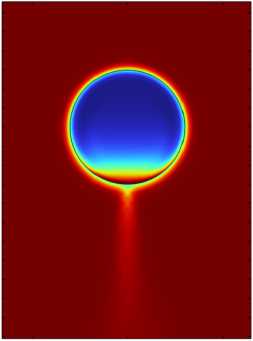
Предварительные расчеты показали, что при вычислении коэффициента поверхностного натяжения на искривленной поверхности критически важно сглаживание. На рисунке 2а показано поле концентрации уксусной кислоты, вычисленное без учета напряжения Марангони в момент времени t = 100 с. На рисунке 2б, в на поверхности капли приведены зависимости от полярного угла φ коэффициента поверхностного натяжения, рассчитанного в соответствии с выражением (4), и напряжения сдвига, вычисленного по формуле (9). Результаты представлены как до, так и после процедуры сглаживания. Из рисунков видно, что даже небольшие отклонения мм

О

-2

-4

-6

-8

моль/м' ,

( a )

-10

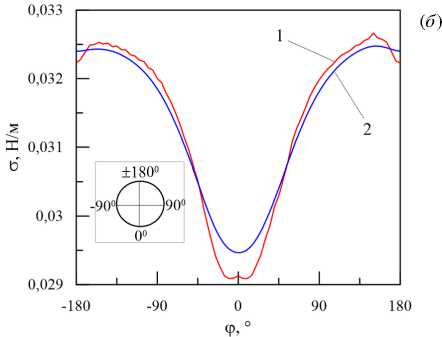
Рис. 2. Поле концентрации уксусной кислоты при k c = 5 · 10 ^{- 6} м/с в момент времени t = 100 c ( а ); зависимости от полярного угла φ коэффициента поверхностного натяжения ( б ) и напряжения сдвига ( в ) на поверхности капли (исходные и сглаженные данные отмечены, соответственно, цифрами 1 и 2 )

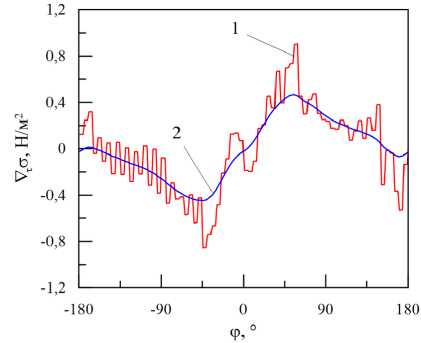
( в )

от гладкого поведения функции поверхностного натяжения вызывают резкий всплеск напряжений сдвига на поверхности. И такая картина наблюдается даже по прошествии довольно длительного времени от момента, когда большие градиенты концентрации, связанные с начальным переходным этапом эволюции, уже сглажены. Рассмотрение динамики на малых временах только усугубляет картину разрывного характера данных. Чтобы решить эту проблему, при вычислении коэффициента поверхностного натяжения проводилось сглаживание с использованием фильтра Гельмгольца:

V^ ( -R 2 VU ) + U = D, (13)

где D — входные данные, U — отфильтрованные данные, R — радиус фильтра (регулировочный параметр). В расчетах полагалось R = 10 ^-3 . Кривые 2 на рисунках 2 б , в соответствуют данным, сглаженным с помощью фильтра Гельмгольца (13) .

• 3.    Численные результаты

Численное моделирование показывает, что описанная выше математическая модель адекватно изображает колебательный режим абсорбции уксусной кислоты каплей воды в условиях внутренней задачи. Приведем результаты расчетов для капли диаметром 6 мм и константой порога возникновения концентрационнокапиллярной конвекции f ₀ = 0.4 Н/м ² . На рисунке 3 представлены зависимости от времени касательного напряжения f _M , измеренного в двух точках со значениями угла ф - 45 ° и 45 ° , что соответствует правой и левой частям поверхности капли. Можно заметить, что релаксационные колебания возникают не мгновенно, а через некоторое время, в течение которого сдвиговое напряжение Марангони достигает критического значения f ₀ . Для параметров, принятых в расчете, это время составляет примерно 45 с.

Каждый период колебания состоит из двух фаз, которые протекают с существенно разными характерными временами. Это приводит к закону колебаний, который сильно отличается от гармонического. Медленный процесс (релаксация) представлен диффузией уксусной кислоты в водном растворе под действием силы тяжести. Быстрый

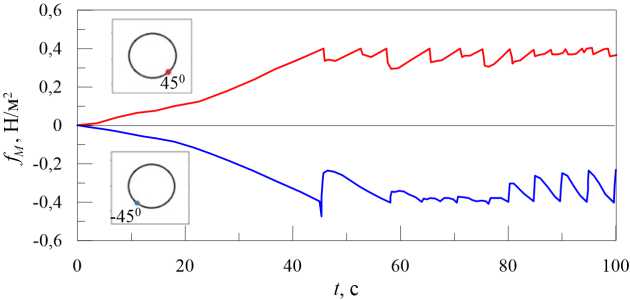
Рис. 3. Изменения касательных напряжений на межфазной поверхности в зависимости от времени для случая f ₀ = 0 . 4 Н/м ² ; данные получены для точек на поверхности капли со значениями полярного угла - 45 ° и45 ^о

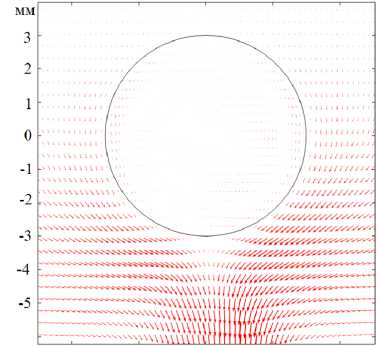
процесс обусловлен вспышкой конвекции Марангони, которая совершает работу по перемещению молекул ПАВ в поле силы тяжести в исходное состояние с более высоким значением потенциальной энергии. В этих условиях период колебаний (порядка 5 с, см. Рис. 3) фактически определяется характерным диффузионным временем, которое необходимо для перемещения молекул ПАВ к нижней части поверхности капли и создания там требуемого градиента концентрации на искривленной межфазной поверхности. Рисунок 4а показывает мгновенные поля скорости, которые возникают на медленном этапе (релаксации), а рисунок 4б — при вспышке конвекции Марангони. В силу непрерывности касательных напряжений на межфазной границе конвективные вихри образуются как внутри капли, так и снаружи. Из рисунка в целом видно, что основные события происходят в нижней части капли, где скапливаются молекулы ПАВ. Уксусная кислота в водных растворах является тяжелой примесью, поэтому в поле силы тяжести молекулы оседают. Для ПАВ, которые ведут себя в воде как легкий компонент (например, спирты), эффект может быть обратным, и колебания будут генерироваться в верхней части капли. Максимальное значение скорости достигается в точках, находящихся примерно под углом -45 ° к вертикали (Рис. 4б ). Обнаружено, что струя жидкости вдоль поверхности, генерируемая неустойчивостью Марангони, не поднимается выше ф = 90 ° , так как величина касательного напряжения падает ниже порогового значения.

( a )

-4       -2        0        2        4 мм

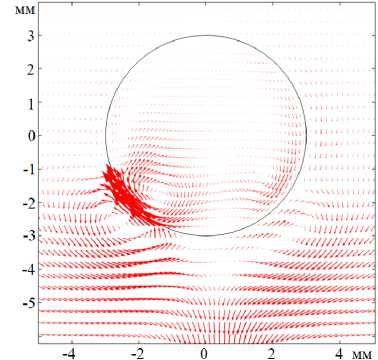
Рис. 4. Поле скорости в момент релаксации ( а ) и сразу после вспышки концентрационной конвекции Марангони ( б ); диаметр капли 6 мм, пороговое значение касательного напряжения f ₀ =0 . 4 Н/м ²

Стоит обратить внимание на то, что в системе есть два конкурирующих осциллятора, так как условия для вспышки конвекции Марангони независимо формируются в левой и правой частях капли. При этом синхронизация колебаний, как правило, не наблюдается. Например, рисунок 4б показывает, как в левой части капли возбуждается концентрационно-капиллярное течение, а правая половина в это время остается, в целом, неподвижной. Развертки по времени, представленные на рисунке 3, иллюстрируют этот вывод. Тем не менее, нелинейное взаимодействие осцилляторов присутствует. На рисунке 3 заметно, что временные окна повышенной активности одного осциллятора сопровождаются подавлением конкурента. Например, между временами 55 и 80 с наиболее ярко проявляет себя правая часть капли, а после 80 с осцилляторы меняются ролями. Нелинейность взаимодействия обусловлена встречными эффектами. С одной стороны, конвективный вихрь отбрасывает молекулы ПАВ вдоль поверхности вверх, но в силу замкнутости течения подтягивает другие молекулы к поверхности из центральной части капли (см. Рис. 4б). Последнее помогает конкурентному осциллятору быстрее сформировать требуемый градиент концентрации ПАВ вдоль поверхности. Однако знак касательных напряжений осцилляторов разный (Рис. 3), что приводит к подавлению одного из осцилляторов при вспышке конвекции у конкурента.

Также на рисунке 4 просматривается слабая гравитационная конвекция, которая обнаруживается как в момент релаксации, так и при вспышке конвекции Марангони. Хорошо этот эффект заметен в правой части капли, причем движение жидкости направлено вниз и внутри капли, и с внешней от межфазной поверхности стороны. Эта конвекция является следствием контракции. Во внешнем растворе, который изначально однороден, уксусная кислота выступает как легкая примесь. Поэтому при диффузии ПАВ внутрь капли (из-за разности химических потенциалов воды и органической смеси капля служит концентратором ПАВ) происходит потеря легкого компонента и снижение плавучести смеси. Начинается движение раствора вниз, которое выглядит как длинная струя под каплей. Подобное явление наблюдается также и в физических экспериментах [5] .

Картины последовательных изменений поля концентрации ПАВ в ходе колебаний показаны на рисунке 5. Представлены фазы релаксации (Рис. 5а), максимального развития конвекции Марангони, которая в этот раз возбудилась почти симметрично с обеих сторон капли (Рис. 5б) и затухания концентрационно-капиллярной конвекции (Рис. 5в). Формирование струи органического растворителя, обедненного молекулами уксусной кислоты, хорошо видно на рисунке. Свой вклад в струю вносит также отдача от затухающего вихря Марангони с внешней стороны межфазной границы (Рис. 5в, вихрь слева). В целом можно заключить, что в процессе массопереноса участвует только нижняя часть капли.

мм

( a )                                               ( б )

ИНН ■ ВЯ ।

о

-2

-4

-б

-8

-10

( в )

О

Рис. 5. Поля концентрации ПАВ в последовательные моменты времени t , с: 40 ( а ), 45 ( б ), 50 ( в ), для f ₀ = 0 . 4 Н/м ²

Обнаружено, что параметр f 0 является бифуркационным. На рисунке 6 показана бифуркационная диаграмма осредненной по периодам амплитуды релаксационных колебаний в зависимости от величины порога f ₀ . Амплитудная кривая имеет типичный вид для бифуркации Андронова–Хопфа. Вблизи порога наблюдаются сильные флуктуации. Возмущения приводят к спорадическим вспышкам слабых колебаний, которые затухают через несколько периодов. Определение амплитуды колебаний сопровождается здесь погрешностью, большей по сравнению с диапазоном параметра, в котором колебания носят уже ярко выраженный устойчивый характер. Точка бифуркации f ₀ ^∗ находится в интервале от 0.15 до 0.2 Н/м ² . В случае, когда на межфазной границе не применяется гипотеза (9) , то есть f ₀ =0, релаксационные колебания в численных экспериментах не наблюдались.

Рисунок 6 иллюстрирует, каким образом подбиралось значение параметра f 0 . Как видно, для возбуждения колебаний требуется выполнение условия f 0 > f 0^∗ , которое гарантирует, что рассматривается процесс выше точки бифуркации. Далее значение f 0 выбирается так, чтобы амплитуда и период колебаний были наиболее близкими к экспериментально наблюдаемым значениям. Параметр f ₀ определяет силу, которая порождает мгновенный конечный импульс, передаваемый межфазной поверхности. От величины этого импульса зависит, как далеко по инерции будет двигаться поверхность и, значит, как долго она будет затем возвращаться в исходное состояние. При вариации f 0 амплитуда и период колебаний меняются в достаточно широких пределах. Например, если значение f 0 сделать слишком большим, то межфазная поверхность по инерции будет смещаться вплоть

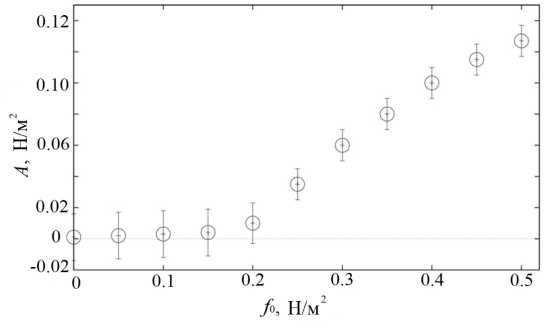
Рис. 6. Осредненная амплитуда колебаний касательных напряжений как функция параметра f 0 , задающего порог начала конвекции Марангони (вычисления проведены для капли диаметром 6 мм)

до верхней части капельки. В то же время экспериментальные данные свидетельствуют (см. [15] ), что поверхность никогда не поднимается выше линии горизонтальной симметрии капли. Значение f 0 было подобрано таким, что в численных экспериментах эти требования выполнялись (см. Рис. 5б ).

• 4.    Обсуждение и заключение

Согласно классическому пониманию концентрационного эффекта Марангони, капиллярная конвекция начинается при любом, сколь угодно малом значении градиента концентрации ПАВ, приложенном к свободной поверхности. При этом формула (9) подразумевает, что градиент сначала должен достигнуть определенного критического значения, после чего возбуждается концентрационно-капиллярная конвекция. В обсуждаемой в данной статье задаче оказывается, что гипотеза (9) является ключевой для описания релаксационных колебаний. Этот вывод может быть переформулирован иным образом. Можно постулировать, что между формированием градиента концентрации ПАВ вдоль поверхности и началом движения этой поверхности должно пройти некоторое время. Альтернативой формуле (9) могла бы быть обратная связь между величиной поверхностного натяжения и скоростью движения жидкости на поверхности, срабатывающая с некоторым характерным временем запаздывания. Такая гипотеза также приводит к возбуждению релаксационных колебаний в математической модели.

Проблема с формулой (9) и любыми подобными гипотезами заключается в том, что они носят феноменологический характер. По сути, отсутствие экспериментально подтвержденной информации о конкретном физическом механизме, который лежит в основе явления, компенсируется известным математическим приемом, гарантированно приводящим к возбуждению колебаний при численном моделировании. Как известно, запаздывание — типичная причина возбуждения колебаний в динамических системах [23] . Отчасти отсутствие информации обусловлено сложностью проведения экспериментальных исследований концентрационных полей, для которых существует небольшой выбор возможностей их визуализации и получения количественных данных [9] . В некоторых работах (см., например, [14] ) приводится гипотетическое объяснение, почему происходит такое неклассическое проявление эффекта Марангони. Как правило, вода содержит неконтролируемые примеси ПАВ (чаще всего органического происхождения), которые с большим трудом поддаются очистке, и большинство экспериментаторов игнорирует эту процедуру. Если примесь попала в двухфазную систему, в которой одна из фаз вода, то она быстро адсорбируется межфазной поверхностью с формированием поверхностной фазы. Когда молекулы контролируемого ПАВ подходят к поверхности, то им требуется время, чтобы выдавить из нее паразитную примесь (что удается сделать, как правило, не до конца). Это объяснение выглядит логичным, но не достаточным. Во-первых, сама декларация того, что в эксперименте присутствует нечто «не контролируемое», уже кардинально меняет результаты физического эксперимента и, с точки зрения методологии науки, выглядит уязвимо. Авторам статьи кажется, что требуется приложение усилий к постановке эксперимента без такого — «не контролируемого» — вмешательства. К сожалению, реализовать это непросто, так как метод Физо-интерферометрии, основной метод для измерения концентрационных полей, хорошо работает только для двойных растворов, а два конкурирующих в растворителе ПАВ уже представляют собой тройной раствор. Во-вторых, ситуация требует от теоретиков создания математической модели, не имеющей в своей формулировке феноменологических допущений того или иного рода. В заключение отметим, что в данной работе численно исследовалась задача о возбуждении релаксационных колебаний внутри квазидвумерной капли воды, имеющей круглую форму и окруженной однородным органическим раствором ПАВ. Показано, что колебания возможно описать только при дополнительном предположении о пороговом характере срабатывания эффекта

Марангони. Показано, что параметр, задающий величину порога, является управляющим параметром бифуркации Андронова–Хопфа. Определена точка бифуркации, выше которой в системе возбуждаются колебания.

Исследование выполнено при финансовой поддержке Российского научного фонда (проект № 19-11-00133), в Пермском национальном исследовательском политехническом университете.