Воздействие продольных и поперечных волн на цилиндрические слои с жидкостью

Воздействие продольных и поперечных волн на цилиндрическое тело исследовалось многими учеными [1, 2, 3, 4]. При этом рассматривались осесимметричные (и неосесимметричные) задачи и применялись различные модели для жидкости и слоя (или оболочек). В предыдущих работах цилиндрическое тело рассматривалось в виде цилиндрической оболочки и уравнение движения было получено на основе гипотезы Кирхгофа – Лява [5, 6, 7, 8]. Окружающая среда рассматривалась как упругая, т.е. связи напряженного и деформированного состояний подчинялись закону Гука [9, 10]. Настоящая работа отличается от предыдущих тем, что цилиндрическую оболочку окружает среда, обладающая вязкими свойствами, т.е. связи напряжения и деформации подчиняются интегральному соотношению Больцмана – Вольтерра [12, 13, 15]. Модели воздействия продольных и поперечных волн на цилиндрические слои и жидкости базируются на методах, которые разработаны для динамики тел, взаимодействующих с деформируемой средой (см., например, книгу [11]).

Постановка задачи

На бесконечно длинный, однородный, изотропно-деформируемый цилиндр с идеальной сжимаемой жидкостью, находящийся

в бесконечно вязкоупругой среде, падает гармоническая плоская волна расширения (или сдвига) (рис.1). Фронт волны параллелен оси цилиндра. Таким образом, рассматривается задача о плоской деформации. Здесь r = R внешний и r = R ₀ внутренний радиусы цилиндрического слоя. Основной целью работы является определение напряженно-деформированного состояния цилиндрического слоя и окружающей среды при воздействии продольных (или поперечных) гармонических волн. В предположении обобщенного плоско-деформированного состояния уравнение движения в смещениях имеет вид [1]

~                _         _   ^

( A j + 2 / ~ j ) grad divu j - р rotrotu j + b j

= P j

“У 2 ^

d Uj

где A j и ц j ( j = 1,2 , j = 1 - относятся к окружающей среде, j = 2 - к слою) - операторные модули упругости

A j f ( l ) = A oj

^р j f ^{( l} ) = P o j

t

f (t) -J RA>( t - T) f (T ) dT

-^

t

f (l) -J R«( t - t ) f (t ) dT

-^

b _j – вектор плотности объемных сил

(bj = 0); f (t) - некоторая функция; pj - плотности материалов, R^i)(t - т ) и R[i)(t - т) - ядра релаксации, koj, ^oj -

мгновенные модули упругости вязкоупругого материала, u i j ( u j , u^ - вектор смещения,

который зависит от r , θ , t . При давлении до 100 МПа движение жидкости удовлетвори-

рость звука в жидкости. Потенциал ϕ ₀ и вектор скорости жидкости связаны зависимостью ^i

V — grad p ₀. Давление жидкости r — R ₀ определяется с помощью линеаризованного интеграла Коши – Лагранжа.

тельно описывается волновыми уравнениями

P = -„C ф

Р РоС0 51

–

для потенциалов скорости частиц жидкости [11]

1 d 2ф V^" =          ■        (2)

2 d 2      1 d 1 d ²

где V — —2- +----+ 2- +--2- — d r2 r d r   r2 d 6 2

дифференциальные операторы в цилиндрических координатах и С о – акустическая ско-

давление жидкости на стенке цилиндрического слоя и ρ о – плотность жидкости. Нормальная компонента скорости жидкости и слоя, при условии безотрывного обтекания жидкости на поверхности их контакта r = R 0 , должна быть равна

Ф d r

d ur 2 dt

^{r — R} 0

^{r — R} 0

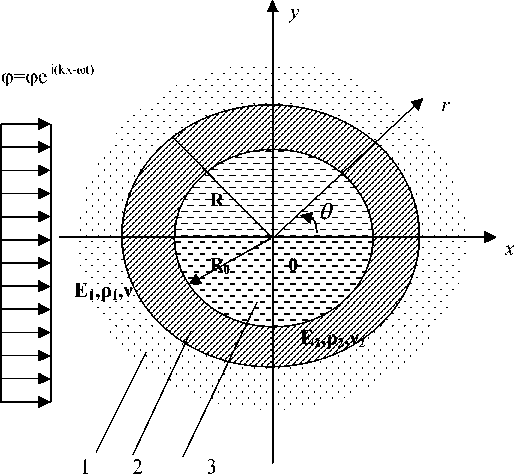
Рис. 1. Расчетная схема с жидкостью 1-вязкоупругая среда; 2- цилиндрический слой; 3-жидкость

где u_{r 2} – перемещение точки слоя по нормали, на контакте двух тел (слоя и окружающей среды). Отметим, что в случае скользящего контакта грунта по поверхности трубы последнее уравнение (2) примет вид [2] ° 61 ^{— 0} .

Пусть падающая плоская волна распространяется в положительном направлении по оси х : ф ^p ) — ф Ае ⁽ a ¹ x '“' ) , ^ 1^p ) — 0 при воздействии продольных волн (или

W 1 p ) — W А е ^{( в} x “' ) , Ф 1 ⁽ p ) — 0 — при воздействии волн сдвига); ϕ_А и ψ_А – величины амплитуды падающих волн; ω – круговая частота падающих волн,

– индекс означает падающие волны. Выражение

ф ^{( p} ) (или w ^{( p} ) ) можно представить в полярных координатах цилиндрического слоя r , θ посредством ряда

»

Р(p’ — Ра S EninJn (a1 r )COS Пве ~1а' , n —1

где

E n

[ 1,

2,

n = 0

n >  1 ,

J _n – цилиндрическая

функция Бесселя 1-го рода.

Методы решения

Поставленная задача решается в потенциалах перемещений, для этого представим вектор перемещения в виде

В результате подстановки уравнения (7) в (5) появятся слагаемые (например, первое уравнение (5)), явно зависящие от времени:

t

- A o j V ² q k ’( r , 0 ) j R [ ^J ' ( t - r ) e ^- “' d r ,

-X

t

- W »V² q k ⁾( r , 0 ) j R' _r ^J ' ( t - r ) e ^- “' d r .

-X

Uj = grad фj + rot у j, (j = 1,2), где ϕj – скалярный потенциал продольных волн; ψ j (ψ rj ,ψθj ) – векторные потенциалы поперечных волн.

Основные уравнения теории вязкоупругости (1) для этой задачи о плоской деформации сводятся к уравнению (Aoj + 2Poj )V2 Vj - tt

- ^oj j RAj )t -' ]^2^jdT - 2Poj j Rj )(t ~T ypjdT =

-X-X

= P j

^Vj dt²

t

Poj^ jJ - Pojj Ri' )t -T )V jjd' = Pj—T. (5) -

На бесконечности r → ∞ потенциалы продольных и поперечных волн (j = 1) удовле- творяют условию излучения Зоммерфельда [1, 10]:

limV1 = 0, lim (Jr) к f^^1 + ia^ ^ = 0, (6) r ^X r ^X                            r            J limj1 = 0, r ^X lim( Tr) к№ r ^X       у dr

⁺ i ^e^ 1

= 0 .

Рассматриваемая задача относится к установившимся процессам колебания [1, 2, 6, 15]. Поэтому решение уравнения (5) ищется в виде

V j ^{( r} , 0 , t ) =

X

= £ qkjV)(r, 0) e -; jj (r, 0 , t) = k = 1

X

= £ q kj " ’( r , 0 ) e ^- “ ' .                    ( 7 )

k = 1

Путем замены переменной t — т =n (5) появляющееся слагаемое можно переписать в виде

- A y?² q J ’( r , 0 ) e -' “ ■

■ j cos “ ■ R^ n ) d n + J sin “ • R j ( n ) d n =

У 0                          0                       7

= - A o j V ² q k ) ( r , 0 ) e - “ ( Г ^ ( “ ) + ir A j “ ) ) .

- P o j V ² q J ’( r , 0 ) e- " •

• j cos “ • J ) d n + J sin “ • R^n ) d n =

У о                          о                       7

= - A j V ² q ^ ¹ ( r , 0 ) e ^- i “ ( Г d “ ) + ir d “ ) ) ,

X

Г у ( a ) = j Ry ( r ) cos ат dT , 0

где

X

Г ? ^{( a} ) = j R J ^{T ) sin aT d T} ,

X

Г ? ^{( a} ) = j ^RJ ^{T ) cos aT d T} .

Такая замена переменных приведена в книге [15, с.38, уравнения (1.54) и (1.55)]. Амплитудной комплексной функции qk(ϕj ) (r,θ) и qk(ψj ) (r,θ), приведенной в (7), удовлетворяют следующие уравнения:

V ²q k ’ > ( r , 0 ) + a 2 q J ) = 0;

v^ l r, e ) + e J<$ = 0,

V ²q koX r , 0 ) + a 0 ²q < ’ ) = 0, J = 1,2 , (8)

₂              ρ_jω ²

где a j = , Л X V .----1.- \

A) j ^{( 1 - A} o j ) ^{+ 2 P} 0 J- ^{( 1 - P} 0 J- )

2      ρjω2         2

ej                 , a о po j (1 - po j )

^ 0 j = Г А) ( ^ ⁾⁺ i ^rAj ( ^ ) , M_Oj = Г _t j ⁽ ^ ^{) +} Г Д ® ) ,

Решение уравнения (8) выражается через функции Ханкеля 1-го и 2-го рода n -го порядка:

^ i L^[ A^ n^{1 ( a} i r ⁾⁺ A ^H() ^{( a} i r ^{) ]} , n = 0

^ 1 = Й BA! e , r ) + BAI e , r ) ] • n = 0

ft IlI ' H^ (a 2 r ) + D - Ht'(a 2 r ) ] , (9) n = 0

V 2 = т\м - ^н”в r ) + L n H^'fa r ) ] , n = 0

P o = L^[ K n J n ^{( a} 0 r ^{) +} K . N n ^{( a} 0 r ^{) ]} , n = 0

где A . , A ’ , B . , B . , C . , D . , L . , M . , К . и K .

– коэффициенты разложения, которые определяются соответствующими граничными условиями (3), (4) и (6); H _n ⁽¹⁾ ( α_j r ) и H _n ⁽²⁾ ( α_j r ) – соответственно функция Хан-келя 1-го и 2-го рода n- го порядка H^² 2 ( ar ) = J . ( ar ) ± iN . ( ar ) . Решение (9) при j=1 удовлетворяет на бесконечности (r→∞) условию излучения Зоммерфельда (6) и представляется в виде

Решение задачи (2), когда r ^ 0 , удовлетворяет условию ограничения силовых факторов [1], отсюда следует, что K . = 0

% = L K.J.(a о r ).

. = 0

Таким образом, подставляя (9) в (7), получим решение уравнения (5) вида

“

P1 =L Ап1 Hn}(a1 r)cos(.° e — ^ , .=0 “ vi =L ci" Н/ч p^ )sin (,ю e- , .=0

^ 2 = jll ^Cn^Hn^{1) ( a} 2^{r )+ D}n^{H (} a ^r jco ne " t , ⁽¹⁰⁾ n = 0

V 2 =£ [ MH в 2 r ) + LH в , r ) ] sin . » ^- “ ' , n = 0

“

% = E K n^J. ^{( a} 0 ^r ) ^cos n^ — ² . . = 0

Полный потенциал можно определить путем наложения потенциалов падающих и отраженных волн. Таким образом, потенциалы смещений будут

ф = p(p) + p^1,ф = ^2, ^1 = V1, ^2 = V2, ф0 = Po (11)

Отсюда следует, что напряжения и смещения легко могут быть выражены через потенциалы смещений [2]

“                      “

P = L А"Н ( a , r ) ; ft = L с н • A r ) .

. = 0                             . = 0

d ф j 1 d v j uri =       +; u^,=

rj d r r d e e

1 d ф j   d у j r le

σ

rrj

σ θθ j

σ r θ j

a o j V

~ o j V

I f 0 j 1

Ф j + ² f o j

^Ф j + ² A ) j

. ’ L Ф r a о a r

a ² ф j a

2 ⁺ a r ² a r

1 , ^{d ф} j 1 a ^{2 ф} j 11 a v j

(+) +       ( r a r r а о          r r а о

1 s ф j] Г 1 a ² v j           a f

2+          22r I r2 а о          [ r 2 а о             a r ^

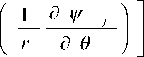
^{d v} )

a r а о

1 a v r a r

Подставляя (11) в (12) с учетом (10), получим следующее выражение для перемещения и напряжения:

^{- 1} yL . j¹ F⁽¹)(„ r\+A F⁾³4ar\+B F⁾³4b       F⁾⁴4a    i^^nOe^i,M

^Ur 1 = ^r L ^AEn¹ E 51 ^{( a} 1 ^{r )+ A}n E 51 ^{( a} 1 ^{r ) +} B n E 52 ^e 1 ^{r )+} K n E 53 ^{( a} 0 ^r В cos " B e ,

. = 0

_u     ^-1       . j¹             F⁾³Ua       (з^ЧВгУ     F'        o^n0e ^iM

^Ue1 = r L WAEn¹ E 61 ^{( a} 1 ^{r )+ A}. E 61 ^{( a} 1 r ^{) +} B n E 62 ^e 1 ^{r )+} K n E 63 ^{( a} 0 ^r в cos ^{n e} e   ,

. = 0

-1                     F)^(a                       F)^ F’^ia ci^nOe iM ur 2 = r  /, CnE 51 \a 2 r) + DnE 61 (a 2 r) + MnE 52 (e 2 r)+ LnE 52 + KnE 53 (a 0 r )J cos nee , n=0

-1(4^4(1       —в?-“ ue 2 = r / CnE 61 (a 2 r ) + DnE 61 \a 2 r ) + MnE 62 (в 2 r ) + LnE 62 (в 2 r ) + KnE 63 (a 0 r )J sin nee n=0

^ rr 1 = 2 ^ 01 ( 1 ^- Д 01 ) r /1<РаЕ_п1^ПЕ n( ^a 1 ^r ) + A . E fffar ) + B n E $^e r ) + K n E ^ ^{( a} 0 r ) ^{] cos} . O e ~^M , n = 0

,

°_вв 1 = 2 B 1 ^{( 1 -} A )1 ) r S ^ A E n i n E 21 ^{( a} 1 r ) ^{+ A}n^E 21 ^{( a} 1 r ) ^{+ B}n^E 232 ) ( Д r ) ^{+ K}n^E 24) ( a r ^{)] cos n e} e ~““ , ⁽¹³⁾ n = 0

° r e 1 = 2 ^ 01 ^{( 1 -} ^ 01 ) r 2 / ^ A E n i n E 4? ^{( a} 1 r ) ^{+ A}n^E « ^{( a} 1 r ) ^{+ B}n^E 42 ) ^{( в} 1 r ) ^{+ K}n^E « ^{( a} 0 r ^{) ] si} n " &^ , n = 0

σ rr2

-X)

= 2^02 (1 — ^02 )r  / n=0

C . E^ a 2 r ) + D „ E «( a 2 r ) + M n E®в 2 r ) + Ь . Е^ в r )

+

σ θθ 2

X

= 2^02 (1 — ^02 )r  / n=0

σ r θ 2

X

= 2^02 (1 — ^02 )r  / n=0

^{+ K}n^E 13" ⁽ a 0 r )

C n E 2’ ( a 2 r ) + D n E 24 ) ( a 2 r ) + M n E ?№ 2 r ) + L . E 22 в r ) +

⁺ K n E 23’ \ a 0 r )

C n E^( a 2 r ) + D n E «( a 2 r ) + M n E 52 ) ( в 2 r ) + L n E Ш r )

+

cos n O e “ t ,

cos n O e “ t

⁺ K . E 54’ ^{( a} 0 r )

sin n e e ^{i №} ,

где

(               2г,- ' A

г ^{( k} )_ _n² , ^{e r} y^{( k)}(ar]-arY⁽k^kЧагУ

^E 11 = ^{n + n          Y}n C r ) ^{a rY}n — 1 ^{( a} r ) ,

к

E ⁽ k ) = n [ ( n + 1 ) Y .^k ’ ( £r ) + prY^r ) ] ,

Ek) =-(n2 + n + ^-a2 r2 Yk\or )+arYka) к 2 j n^

, e 221 = n e>Yk '(er)-(n+1X1 k '(er)].

EJk>= a2r2 -в- Yn■>(ar), к

E 4 k ) = n [ ( n + 1 ) Y , ^k ) ( ar ) - arY^ (ar ) ] ,

E 4 k )=- n ² + n - E— Y _n ^k ) в ) + в Н ^k 1 ( e r )

к

,

^E 5 k ’ = ^[ »r ^Y.^l !( » ^r ) - ^nY, ^{)( a} r ) ] .

e 52 ’ =- nY»e ) ,

E ?=- nY . (ar ) ,

E 52 ) = [ .Y,^{1 2} ) ( £, -) - PY^e ) 1 k = 1,2,3,4 , где

Y(1) _ Г    y(2) _ у    У(3) _        y(4) _ T/M n . , Yn Y'n, Yn 1Yn , :„      .!. .

Неопределенные       коэффициенты

A ..j ) , B ,j ) , C .j ) , D .j ) определяются из системы линейных алгебраических уравнений седьмого порядка       [ ^c ] { q } = [ f ] ,         (1 ⁴ )

где { q } – вектор-столбец, содержащий произвольные постоянные; {F}– вектор столбец внешних нагрузок; [C] – квадратная матрица, элементы которой выражаются через функции Бесселя и Ханкеля. Уравнение (14) решается методом Гаусса с выделением главного элемента.

При r >  0 :

H r . =

—

= ± — In z - i f1 f 1 - — In z ] + 0 ( z ⁴ In z ),

П к 2 j к П               ^Л

H^ ’( z ) r . =

= + - (z 1 {(n -1)!+ n! z2 + 0(z4)}, п к 2 7

и r >  x :

1/2

H ( 1 ^{) ,} ( 2 ) ( _z ) = I ² I     e ± i ^{( kz - n} /4 )

т          к nz j использованы асимптотические формулы Ханкеля 1-го и 2-го рода [14]. В работе перемещение и напряжение сводятся в безразмерных видах:

rj                               θj                              rrj urj = 7------; uej = 2------; ^rr = —;

i α ₁ ϕ _A          i α ₁ ϕ _A            σ ₀

σ r θ j                       2

° е = —; ° 0 =^- в 0 j ^e pa .

σ ₀

Результаты расчетов и выводы

Все выражения для напряжений и смещений имеют вид

(R + i Im)e- :t = (R2 + Im2 )1/2 e-i(at-Y), где co - частота гармонических волн, т.е. заданная действительная величина.

Для данных падающих волн напряжения и смещения определяются рядами, описываемыми с помощью специальных цилиндрических функций Бесселя и Ханкеля, с увеличением аргумента которых функциональные ряды (9), (10) и (13) сходятся.

В качестве ядра релаксации вязкоупругого материала примем трехпараметрическое ядро

А е - et

R (_t ) = R (t ) = R, ( t ) = Aje- .

Л J           M J          J          t 1-a

Ржаницына – Колтунова, где Aj ,α, β – параметры ядра релаксации [3]. Вычисления были выполнены на компьютерном про- граммном комплексе "Matlab", ряды вычислены с точностью до 10-8.

Примем следующие параметры:

A 1 = 0,048; в = 0,05; a = 0,1 ;

A 2 = 0; С 0 = 1493 м; p 0 = 1000 4;

с               м3

E_m i = 2,1 • 10 10 4;

м2

P 1 = 2,0 • 10 3 4; V 1 = 0,25;

м 3

E m2 = 1,95 • 10¹¹—;

м p 2 = 7,86 40114; v 2 = 0,3; R 0 = 0,5 R. м3

Максимальное напряжение в слое с жидкостью на действие продольных и поперечных гармонических волн является радиальным. Их изменение по окружности θ приведено в табл. 1 и 2.

Таблица 1. Радиальное напряжение в слое с жидкостью при воздействии продольных волн

θ	00	450	900	1350	1800
σ rr Пустой слой	0,672	0,423	0,711	0,518	1,65
σrr Слой с жидкостью	0,778	0,435	0,721	0,547	1,686

Таблица 2. Радиальное напряжение в слое с жидкостью при воздействии поперечных волн

	Угол: θ	0 0	450	900	1350	1800
	σ rr Пустой слой	0,631	0,712	0,521	1,801	0,847
	σ rr Слой с жидкостью	0,683	0,914	0,637	1,925	0,886
В области длинных волн (— >  1 , D =2R λ – диаметр слоя, λ – длина волны) напряжения в слое с жидкостью и без жидкости отличаются до 14%, а в области коротких волн (— ( 1 ) - до 40 %. Учет вязких свойств мате-				риала окружающей среды при действии продольных и поперечных гармонических волн снижает напряжение и перемещение на 10– 16%. При 0 = 90 и 2700 достигается максимальное радиальное напряжение при воздействии продольных волн. Следует отметить,
				что максимальное напряжение			при воздейст-
λ				вии поперечных волн достигается при 0 = 45 и

135^0.. Распределение напряжения при β 1 R 1 = 0,099 стремится к статическому случаю (λ→ ∞), в то время как при более высоких волновых ( β ₁ R ₁ = 1,5 ) числах распределение напряжений значительно отличается от статического. Отношение плотностей η = ρ 1 / ρ 2 оказывает большое влияние на напряжение и смещение слоя. По мере возрастания плотности слоя максимальные величины напряжения и смещения слоя возрастают.

Таким образом, разработанная методика и алгоритм для решения поставленных задач позволяют найти напряженно-деформированное состояние цилиндрических тел при воздействии гармонических волн.