Выбор интервала наблюдения для криминологического интервального прогнозирования

Прогноз лежит в основе любого планирования и проектирования [1, с. 355]. Чем точнее прогноз, тем более обоснованны принимаемые на его основе решения. Востребованная для составления краткосрочных и среднесрочных криминологических прогнозов технология трендового прогнозирования является одним из вариантов статистической экстраполяции. Прогноз основывается на распространении закономерности развития изучаемого социального явления за пределы интервала времени, на котором зафиксированы известные данные (за пределы интервала наблюдения).

Преступность, как и любое социальное явление, подчиняется социологическим закономерностям [2, с. 106]. Поскольку преступность – это социальное явление, то на нее оказывают влияние различные социально-экономические факторы: социальные нормы и культура, ситуация в экономике, правоохранительная деятельность, совершенствование уголовного законодательства, деятельность средств массовой информации, общественное мнение и другие факторы. Изменение каждого из указанных факторов происходит не мгновенно, а относительно медленно. Все эти факторы в совокупности создают достаточно большую инерционность изменения уровня преступности.

Исходными данными для криминологического прогнозирования на основе тренда служат, как правило, сведения статистических учетов и официальной отчетности. Такие данные несложно подобрать для любого интересующего интервала наблюдения.

Известные исследования не дают однозначных указаний по выбору интервала наблюдения для интервального прогнозирования. Отдельные исследования содержат общую рекомендацию – принимать длину периода прогнозирования, т. е. срока удаления прогнозируемого уровня во времени от конца базы расчета тренда не более трети, в крайнем случае – половины длительности интервала наблюдения [3, с. 187; 4, с. 124]. Если следовать этой рекомендации, то для прогноза на два года нужен интервал наблюдения не менее шести лет. Однако интервал наблюдения «не менее 6 лет» может иметь следующие значения: 6 лет, 10 лет и 20 лет. Из математической статистики известно, что объем выборки (количество используемых для составления прогноза данных) оказывает значительное влияние на точность оценки статистических показателей, ширину доверительных интервалов и статистическую значимость трендовых моделей [5, с. 126]. При прочих равных условиях увеличение объема выборки приводит к более точным и надежным результатам, но также важно учитывать особенности анализируемых данных.

Данное исследование проводится с целью определения значимости влияния интервала наблюдения на ошибку прогноза и выработки рекомендаций по выбору интервала наблюдения для криминологического прогнозирования на основе тренда.

Для исследования значимости влияния интервала наблюдения на ошибку прогноза рассмотрим задачу краткосрочного прогнозирования количества преступлений в Забайкальском крае (далее – количество преступлений). Сведения о количестве зарегистрированных в Забайкальском крае преступлений доступны в отчетах «Состояние преступности в России», размещенных на официальном сайте МВД России1.

Для исследования выбран интервал наблюдения с 2010 по 2023 год. Исходные данные приведены в табл.1.

Таблица 1

Исходные данные

Год	Количество преступлений	Год	Количество преступлений	Год	Количество преступлений
2010	28991	2015	33373	2020	22703
2011	30485	2016	29658	2021	21707
2012	31287	2017	26992	2022	20816
2013	35001	2018	24341	2023	18441
2014	32150	2019	23573	–	–

На представленной на рис. 1 графической интерпретации исходных данных отмечается как рост, так и снижение количества преступлений, а также имеются локальные экстремумы – в 2013, 2014 и 2015 годах меняется направление изменения данных (после роста отмечается снижение или начинается рост после снижения).

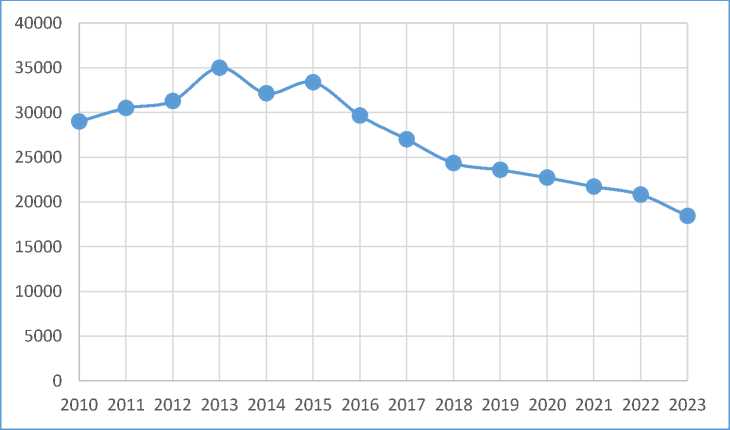
Рис.1. Графическая интерпретация исходных данных

О. Г. Деменченком, С. А. Барановым показано, что интервальное прогнозирование по сравнению с точечной оценкой предоставляет более полную и надежную информацию для принятия решений и оценки рисков, поэтому оно предпочтительнее точечной оценки прогноза [6, с. 175]. В связи с этим в данном исследовании ограничимся трендовыми моделями, которые дают возможность интервального прогнозирования: линейной, квадратичной, кубической и показательной (показательная модель приводится к линейному виду при помощи логарифмирования):

• y = a • x + b ,

• y = a • x² + b • x + c,

• y = a • x³+ b • x² + c • x +d,

• y = a • b ^x ,

• где y - количество преступлений (в тысячах), x - номер года ( x = 1 для самого раннего года интервала наблюдения).

При решении практических задач важно оценить погрешность прогноза [7, с. 28]. Одно из преимуществ статистического подхода к анализу временных рядов состоит в том, что в нем оценка неопределенности рассчитывается по строгим аналитическим формулам [8, с. 405]. Так, интервальная оценка погрешности прогноза основана на расчете ошибки прогноза. Для линейной, квадратичной и кубической модели эта ошибка находится по формулам [9, с. 138]:

J 1 к²

• ^{1    +} n ⁺ fF'

I    к²   ft⁴

- (2ft²)k² +n^k⁴

nft⁴-(ft²)²    '

A— ^ta '^l^{1 +}f [ 2 ⁺

-2Zt 4 )k² + (ft²)k⁶

Zt²ft⁶-(f t⁴)²     '

из рассмотрения ввиду недостаточной статистической значимости уравнения модели (примем уровень значимости 10 % или а = 0,1).

• 3.    Вероятность принятия нулевой гипотезы для коэффициентов модели (Р-значение) - вероятность справедливости гипотезы о равенстве коэффициента модели нулю (т. е. данное слагаемое уравнения модели не обеспечивает статистически значимого объяснения зависимой переменной, модель непригодна для использования). Будем считать непригодной для прогнозирования любую модель, если хотя для одного из ее коэффициентов Р-значение окажется больше 0,1 (уровень значимости 10 %).

Для выявления значимости влияния интервала наблюдения на ошибку прогноза проведем расчеты с использованием разных интервалов наблюдения. Начнем с интервала наблюдения в три года, затем постепенно будем увеличивать интервал на один год.

Для интервала наблюдения в три года невозможно провести регрессионный анализ квадратичной и кубической модели ввиду того, что степень свободы (разность между количеством наблюдений и количеством коэффициентов модели) меньше единицы. По той же причине невозможно провести регрессионный анализ кубической модели для интервала наблюдения в четыре года.

Результаты регрессионного анализа приведены в табл. 2. В таблицу включены результаты для интервалов наблюдения длиной 3, 4, 5, 6 и 7 лет, а также оценка ошибки прогноза на один год. Используемое в расчете ошибки прогноза критическое значение t-статистики Стьюдента зависит от принятого уровня значимости а = 0,1 и степени свободы. Следует отметить, что с ростом длины интервала наблюдения увеличивается степень свободы (разность между количеством наблюдений и количеством коэффициентов модели), что приводит к уменьшению критического значения t-статистики Стьюдента. Таблицы критических значений t-статистики Стьюдента можно найти в справочниках по статистике (также эти значения можно рассчитать в Microsoft Excel с помощью функции СТЬЮДРАСПОБР).

Все полученные регрессионные модели обеспечивают высокую точность описания исходных данных - значения коэффициента детерминации находятся в пределах от 0,93 до 0,99. Это означает, что любая из приведенных в табл. 2 моделей объясняет более 90 % изменений исходных данных. В рамках регрессионного анализа предполагается, что оставшиеся 1–7 % вариации данных вызваны неучтенными в модели случайными факторами. Справедливость этого предположения подтверждена путем проверок гипотез о равенстве нулю суммы ошибок аппроксимации, а также о соответствии распределения ошибок аппроксимации нормальному закону распределения.

Полужирным шрифтом в табл. 2 выделены значения показателей, обусловившие исключение модели из рассмотрения. Значимость критерия Фишера превысила 10 % для линейной модели при длине интервала наблюдения n = 3 и квадратичной модели при n = 4, и эти модели были исключены. Увеличение объема выборки, который для рассматриваемой задачи совпадает с длиной интервала наблюдения, повышает статистическую значимость трендовых моделей. Это несложно заметить по приведенным в табл. 2 численным значениям: значимость критерия Фишера (т. е. вероятность того, что модель статистически незначима) существенно снижается с ростом интервала наблюдения.

Также исключен из рассмотрения ряд квадратичных и кубических моделей из-за того, что вероятность справедливости гипотезы о равенстве отдельных коэффициентов модели нулю превысила уровень значимости 10 %. Это объясняется тем, что в рассматриваемой задаче указанные модели по сравнению с линейной не всегда обеспечивают статистически значимое повышение точности описания исходных данных.

Таблица 2

Длина интервала наблюдения	Модель	R2	Значимость F	Коэффициенты модели	P-значение	Ошибка прогноза при α =0,1
3	линейная	0,94	0,16	–	–	–
3	показательная	0,99	0,01	-0,043 3,165	0,01 0,0004	6,33
4	линейная	0,94	0,03	-1,368 24,33	0,03 0,0008	2,53
4	квадратичная	0,99	0,11	–	–	–
4	показательная	0,93	0,04	-0,067 3,204	0,04 0,0001	3,06
5	линейная	0,95	0,005	-1,215 25,09	0,005 0,00002	1,80
5	квадратичная	0,99	0,01	-0,207 0,03 23,64	0,15 0,96 0,001	–
5	кубическая	0,99	0,07	-0,113 0,811 -2,641 25,54	0,30 0,36 0,31 0,03	–
5	показательная	0,93	0,01	-0,058 3,235	0,01 0,000002	2,46
6	линейная	0,95	0,001	-1,108 25,81	0,001 0,000001	1,53
6	квадратичная	0,99	0,002	-0,145 -0,093 24,45	0,07 0,82 0,00003	–
6	кубическая	0,99	0,007	-0,058 -1,918 0,459 25,90	0,18 0,26 0,18 0,001	–
6	показательная	0,93	0,002	-0,052 3,264	0,002 0,000000	2,22
7	линейная	0,96	0,0001	-1,235 27,59	0,0001 0,000000	1,61
7	квадратичная	0,96	0,002	0,006 -1,283 27,67	0,94 0,10 0,00001	–
7	кубическая	0,99	0,0005	-0,088 1,059 -4,882 30,83	0,01 0,01 0,01 0,00003	2,99
7	показательная	0,96	0,0001	-0,055 3,334	0,0001 0,000000	2,09

В этой задаче квадратичная и кубическая модели в целом оказались малопригодны для прогнозирования, а отдельные подходящие для прогнозирования варианты моделей приводят к относительно большой ошибке прогноза. Так, для интервала наблюдения 7 лет ошибка прогноза кубического тренда составила 2,99, что больше соответствующих ошибок для линейного и показательного тренда – 1,61 и 2,09, поэтому квадратичная и кубическая модели исключены из рассмотрения.

Минимальной оказалась ошибка прогноза линейной модели при длине интервала наблюдения 6 лет – 1,53. Дальнейшее увеличение длины интервала наблюдения от 8 до 14 лет не привело к уменьшению ошибки прогноза. Зависимость ошибки прогноза по линейной и показательной модели при α = 0,1 от длины интервала наблюдения представлена на рис. 2.

Полученные в ходе решения задачи результаты свидетельствуют о существенном влиянии длины интервала наблюдения на ошибку прогноза – для различных трендовых моделей на интервале наблюдения от 3 до 14 лет отмечено изменение ошибки прогноза в 3,3–3,6 раза:

ошибка прогноза линейного тренда изменяется в 3,6 раза в пределах от 5,52 при n = 14 до 1,53 при n = 6;

ошибка прогноза показательной модели изменяется в 3,3 раза в пределах от 6,33 при n = 2 до от 1,91 при n = 11.

Следовательно, изменение интервала наблюдения способно кратно изменить ошибку прогноза.

Следуя общим рекомендациям, для прогноза на один год нужно выбрать интервал наблюдения не менее трех лет. Ошибка прогноза для интервала из трех лет составила 6,33, что в 4,1 раза превышает минимальное значение. Линейная модель для интервала наблюдения три года оказалась статистически незначимой, а для интервала наблюдения четыре года ошибка прогноза на 65 % больше минимального значения. Следовательно, правильный выбор интервала наблюдения может существенно повысить точность интервального прогноза.

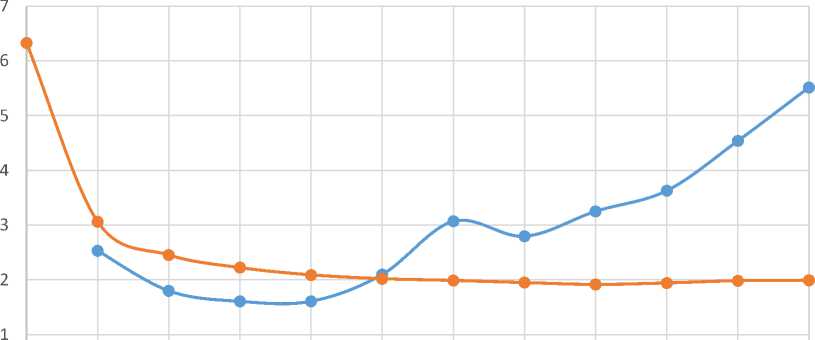
3       4       5       6       7       8       9       10      11      12      13      14

линейная модель        показательная модель

Рис. 2. Зависимость ошибки прогноза на один год при α = 0,1 от длины интервала наблюдения

В рассматриваемой задаче наиболее точный прогноз обеспечивает линейный тренд, полученный на интервале наблюдения 6 лет.

Точечная оценка прогноза получается при подстановке в уравнение модели номера года x = 7 (номер года, следующего за интервалом наблюдения):

у = -1,108 x + 25,81 = -1,108 ■ 7 + 25,81 = 18,054.

Тогда интервальный прогноз будет соответствовать интервалу:

у ± А = 18,054 ± 1,53 = 16,524   19,584.

Прогнозируем, что количество преступлений в Забайкальском крае в 2024 году с вероятностью 90 % окажется в интервале от 16,524 до 19,584 тысячи.

Авторы полагают, что оптимальная длина интервала наблюдения зависит от характера исходных данных и используемой модели прогнозирования. Для получения наиболее точного интервального прогноза рекомендуется провести расчеты с переменной длиной интервала наблюдения на основе различных моделей и выбрать пригодный для прогнозирования вариант по критерию достижения минимальной ошибки прогноза.

Исходя из изложенного, можно сделать следующие выводы:

длина интервала наблюдения может оказывать значительное влияние на ошибку прогноза, в отдельных случаях приводя к кратному изменению ее величины;

правильный выбор интервала наблюдения способен существенно повысить точность интервального прогноза;

выбор длины интервала наблюдения рекомендуется проводить на основании результатов пробных расчетов с переменной длиной интервала наблюдения, приняв в качестве критерия выбора условие достижения минимального значения ошибки прогноза.