Вычисление тензора эффективной массы в ε- и ξ-фосфорене методом теории функционала плотности

DOI:

Фосфорен, однослойная форма фосфора, привлекает внимание исследователей необычными физическими свойствами (высокая подвижность зарядов, оптическое и УФ-поглощение) и возможностью практического приложения в оптоэлектронике [10; 11]. В отличие от графена, у фосфорена есть запрещенная зона. Ширина запрещенной зоны фосфорена находится в Γ -точке зоны Бриллюэна, при этом вершина валентной зоны почти плоская. С точки зрения применения в оптоэлектронике, наличие запрещенной зоны с прямыми переходами представляет собой преимущество, поскольку легче изготавливать стабильные устройства [11].

Черный (α-P) [6] и синий фосфорен (β-P) [12] являются наиболее стабильными аллотропами семейства фосфора. В ряде работ, например [5], черный фосфорен рассматривается как типичный пример двумерного материала с сильной анизотропией зоны проводимости. Как новый потенциальный полупроводниковый материал, синий фосфорен демонстрирует преимущество своей широкой непрямой запрещенной зоны. Кроме того, были предложены другие аллотропы, в том числе ε-P, ξ-P. Согласно теоретическим исследованиям, эти аллотропы обладают разнообразными электронными, оптическими и механическими свойствами, что открывает возможности для создания новых наноустройств [3; 7; 9]. На рисунке 1 показана кристаллическая структура фосфорена [4].

В работе был рассчитан тензор эффективной массы для различных аллотропов фосфорена. Для проверки корректности рассчетов были рассмотрены ранее изученные модификации — α-P и β-P. Далее полученные методики были применены к двум малоизученным модификациям, что поможет детально изучить отклик носителей заряда на внешние поля в их зоне проводимости. Исследования зонной структуры фосфорена проводились с использованием пакета OpenMX (Open source package for Material eXplorer) — программы для моделирования наноразмерных материалов на основе теории функционала плотности (англ. density functional theories (DFT)) [8]. В работе использовались следующие параметры рассчета: в качестве базиса атомных волновых функций брались оптимизированные функции PAO (Polarized atomic orbital), обменно корреляционный потенциал PBE. Элементарная ячейка берется согласно рисунку 1 c параметрами из таблицы 1.

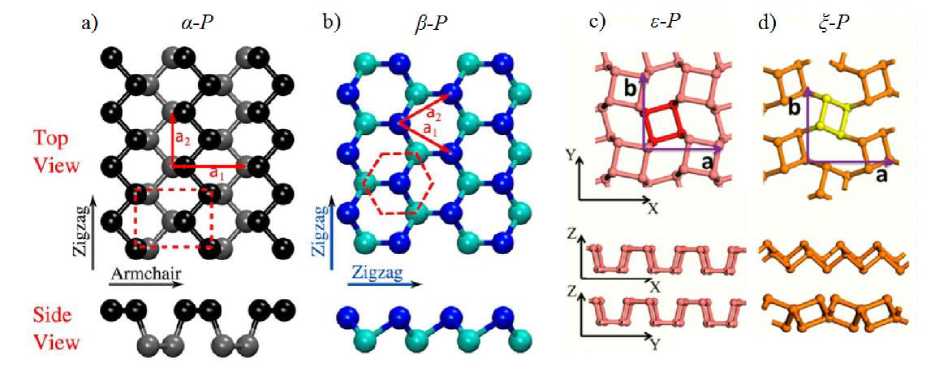
Рис. 1. Кристаллическая структура a) α-P; b) β-P [4]; c) ε-P; d) ξ-P [7]

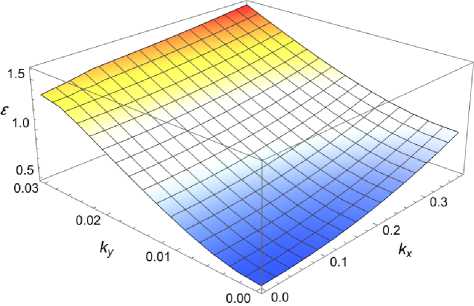
Рис. 2. Закон дисперсии носителей тока в зоне проводимости α-P вблизи Γ -точки.

Проекции волнового вектора к _х ,к _у измеряются в единицах 2 п/а 1 , 2

В таблице 1 представлены параметры решетки для разных типов фосфорена. На рисунке 2 показан закон дисперсии носителей тока в зоне проводимости фосфорена вблизи Г -точки зоны Бриллюэна, рассчитанный с помощью пакета OpenMX в рамках теории функционала плотности.

Таблица 1

Параметры решетки различных типов фосфорена

	α -P	β -P	ε -P	ξ -P
а 1 , A	3,299	3,15	5,403	6,47
0 2 , A	4,62	3,15	5,403	5,35

На основе интерполяции полученной при помощи DFT-расчета зависимости, показанной на рисунке 2, был рассчитан тензор обратной эффективной массы (в единицах обратной массы свободного электрона):

С—)

V т ! Х,у

1 Э2Е к2 дкхдку'

Тензор эффективных масс для α-P имеет вид:

1, 285    0, 0

0, 0    0,125

)■

Из (2) видно, что эффективные массы во взаимно перпендикулярных направлениях в фосфорене сильно отличаются, что означает резкую анизотропию его кинетических коэффициентов.

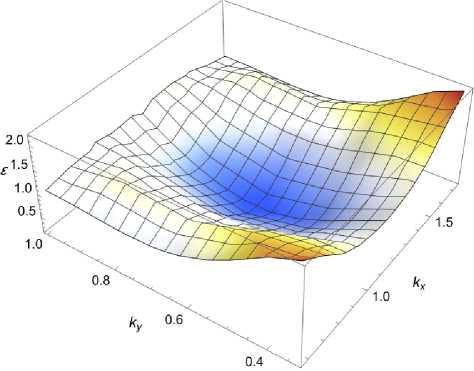
Рис. 3. Закон дисперсии носителей тока в зоне проводимости β-P вблизи K -точки.

Проекция волнового вектора к _х измеряется в единицах п/ 3 о 1 , проекция к _у — в единицах 2 n/ 3 V 3 a 2

В отличие от α-P, β-P имеет изотропную структуру, что отражается в значениях тензора эффективной массы, рассчитанных в К-точке (рис. 3):

0, 341    0, 0

0, 0   0, 339

Тензоры (2) и (3) хорошо коррелируют с полученными ранее при помощи других методов и программного обеспечения [2], что показывает корректность проведенных нами расчетов при помощи OpenMX.

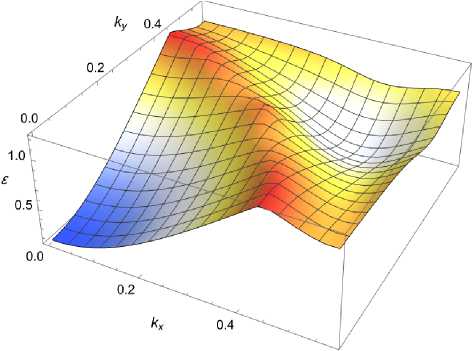
Рис. 4. Закон дисперсии носителей тока в зоне проводимости ε-P вблизи Γ -точки. Проекции волнового вектора к _х ,к _у измеряются в единицах 2 п/а 1 , 2

Рассмотрим теперь тензоры обратной эффективной массы для ε-P и ξ-P. Расчет показывает, что ε-P имеет схожую с β-P структуру зоны проводимости, спектр ε-P изотропен, но имеет минимум в Γ -точке (рис. 4):

0,445   0, 0

0, 0   0,446

В свою очередь, ξ-P ближе по структуре к α-P (рис. 5). Тензор обратных эффективных масс ξ фосфорена имеет вид:

3,127

1,452

1,452

4,187

)•

После приведения к главным осям и масс:

обращения получаем тензор эффективных

0, 474   0, 0

0, 0    0,192

Полученные результаты будут использованы в дальнейших исследованиях. В частности анизотропия тензоров эффективных масс в α- и ξ-фосфорене может привести к ярким особенностям фотогальванических эффектов.

В свою очередь, наличие непрямой запрещенной зоны в ξ-фосфорене приводит к возможности проявления в этом материале сильного акусто-электрического эффекта.

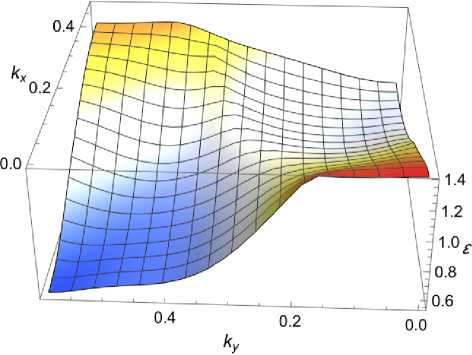
Рис. 5. Закон дисперсии носителей тока в зоне проводимости ξ-P вблизи минимума. Проекции волнового вектора к _х ,к _у измеряются в единицах 2 п/а 1 , 2

Для расчетов был использован кластер ВолгГТУ [1].

ПРИМЕЧАНИЕ

• ¹    Работа выполнена при поддержке гранта ВолгГТУ № 54/470-22.