Выявление спектрально локализованных компонент на частотах лунных приливов во временных рядах вертикальной составляющей электрического поля пограничного слоя атмосферы земли

В результате многолетних наблюдений было установлено, что увеличение интервала, анализа при использовании классической квадратурной схемы спектрального анализа не позволяет выявить воздействие лунных приливов па. электромагнитное поле в приземном слое атмосферы. Как было показано в дальнейшем [12], это является следствием иекогереитиости выявляемых составляющих. В связи с этим дальнейшие исследования воздействия приливных процессов па. электромагнитное поле Земли велись с использованием анализатора собственных векторов и компонент сигнала [3], показавшего свою эффективность при выделении из экспериментальных временных рядов энергетически педомипирующих квазипериодических составляющих.

В данной статье исследовались четыре временных ряда. (ВР) многолетних наблюдений вертикальной составляющей электрического поля Ez пограничного слоя атмосферы: данные экспериментального полигона, кафедры общей и прикладной физики ВлГУ (2003-2009 гг.); данные геофизических обсерваторий Душети (1976-1980 гг.), Воейково (1966-1995 гг.), Верхнее Дуброво (19741995 гг.).

Обработка ВР велась с использованием анализатора собственных векторов и компонент сигнала (АСВиКС) [3], конструкция которого представлена, па. рисунке 1. На. вход блока масштабирования 1 поступает анализируемый временной ряд Xt (1 ^ t ^ N); в блоке 2 вычисляется ковариационная матрица R временного ряда Xt на заданном интервале анализа длины M отсчётов ВР; в блоке 3 производится вычисление собственных векторов ^i и собственных значений Ai (1 ^ i ^ M); в блоке 4 осуществляется анализ собственных векторов t//i и собственных значений Ai — с целью выявления характерных признаков и оценки параметров искомых физических явлений. Ковариационная матрица R в блоке 2 вычисляется с использованием соотношения

YY'

(0.1)

N - M + 1 ’ в котором Y — так называемая траекторная матрица [4]

X1

X n -м +1

X n -M +2

XN-M +3

...

XN

(0.2)

X 2

Хз

......

. Хм Хм +1

Столбцы траекторной матрицы Y представляют собой отрезки ВР, получаемые путём перемещения по нему с единичным шагом интервала анализа длительностью M отсчётов.

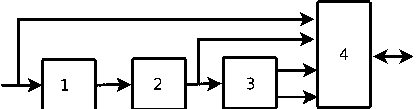
Рис. 1. Анализатор собственных векторов и компонент сигнала [3]. 1 — блок масштабирования.

2 — вычислитель ковариационной матрицы. 3 — вычислитель собственных векторов и собственных

значений. 4 — анализатор признаков и компонент временного ряда.

BP Xt на любом из различных интервалов анализа длительности M может быть представлен в базисе собственных векторов ^i ковариационной матрицы R (образующих ортонормированный базис [5]), который определяется соотношением

R$i = Ai-$i, 1 < i < M.(0.3)

Нетрудно показать, что средняя энергия E ВР, наблюдаемого на интервале анализа, определяется соотношением

MM

E = £гм = TrR =     ,(0.4)

i=1

где ri,i — i-ый диагональный элемент ковариационной матрицы R,

TrR — след ковариационной матрицы R.

Собственные векторы, таким образом, представляют собой ортонормированные некоррелированные компоненты анализируемого на интервале M ВР, вносящие в среднюю энергию E анализируемого ВР относительный вклад

А™^р “• =     ^A .                                     (0.5)

i     EM Ai

Последовательность собственных значений Ai, упорядоченную по их убыванию, будем называть спектром собственных значений (ССЗ), а соответствующую ей последовательность (0.5) — нормированным спектром собственных значений (НССЗ).

АСВиКС относится к классу анализаторов с адаптивным базисом; базис, в котором осуществляется представление ВР на конечном интервале анализа, зависит от самого ВР. Нетрудно показать (с использованием известных теорем линейной алгебры [5]), что представление в базисе собственных векторов (СВ) при заданной точности представления ВР на интервале анализа требует наименьшего числа компонент, то есть обладает наибольшей выразительностью. При этом сами СВ несут в себе информацию о структуре исследуемого ВР. Так, при наличии во ВР спектрально локализованных компонент, СВ будут содержать в себе эти компоненты, которые могут быть обнаружены с использованием стандартных средств спектрального анализа. Показано [6], что спектральный анализ СВ обладает большей чувствительностью, чем классический спектральный анализ ВР, особенно в тех случаях, когда компоненты не являются абсолютно когерентными. АСВиКС во многих случаях позволяет выявлять тип анализируемого ВР по форме НССЗ [3].

Использование АСВиКС целесообразно в тех случаях, когда использование классической квадратурной схемы спектрального анализа вызывает затруднения, например, в силу некогерентности

ВР. На рисунках 2, 3 приведены в двойном логарифмическом масштабе оценки амплитуды спектральной составляющей с частотой солнечного прилива S1 (рисунок 2) и частотой лунного прилива 2N2 (рисунок 3), полученные с использованием классической квадратурной схемы для ВР станции Воейково.

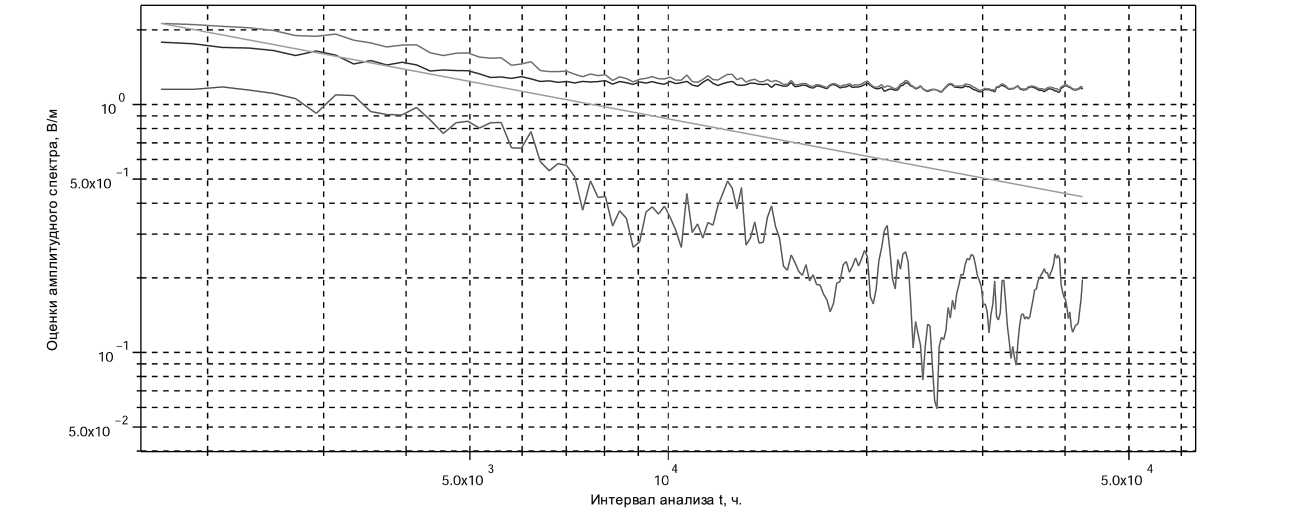
Рис. 2. Зависимость оценки спектральной составляющей на частоте солнечного прилива S1 от длительности интервала анализа при использовании квадратурной схемы. Верхняя кривая — действующее значение, средняя кривая — выборочное среднее, нижняя кривая — выборочная дисперсия. Прямая ~ 1/Vt, где t — длина интервала анализа

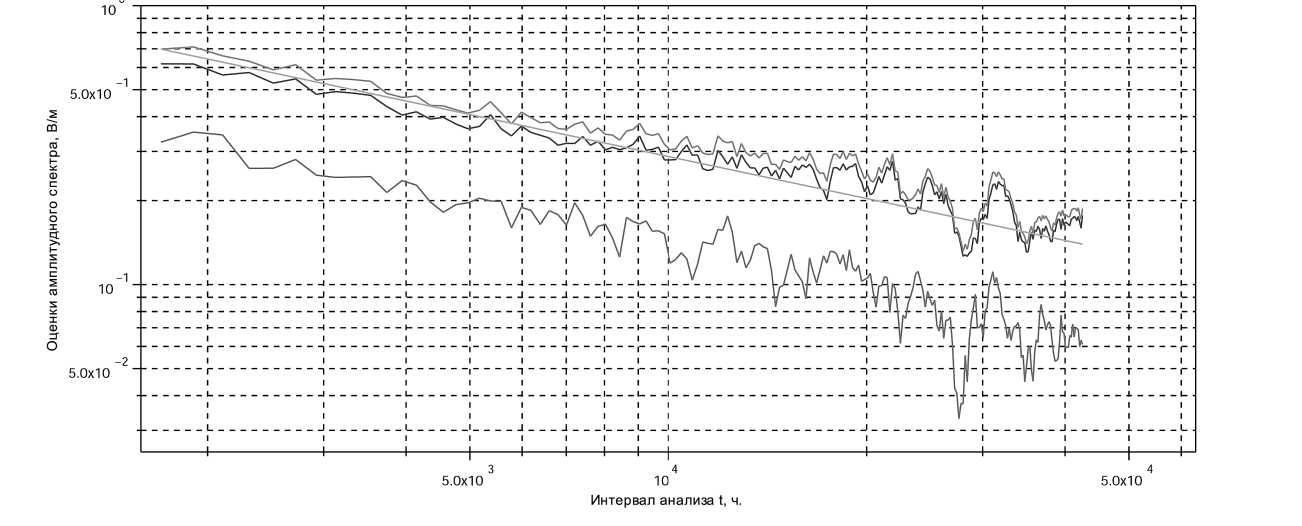
Рис. 3. Зависимость оценки спектральной составляющей на частоте лунного прилива 2N2 от длительности интервала анализа при использовании квадратурной схемы. Верхняя кривая — действующее значение, средняя кривая — выборочное среднее, нижняя кривая — выборочная дисперсия. Прямая ~ 1/Vt, где t — длина интервала анализа

Как видно из рисунка 2, выявление составляющей с частотой солнечного прилива с использованием квадратурной схемы не вызывает затруднений — выборочное среднее и действующее значение сходятся к некоторому ненулевому фиксированному значению, а дисперсия спектральной оценки монотонно падает с увеличением интервала анализа. Для составляющей с частотой лунного прилива (рисунок 3) ситуация иная — по мере роста интервала анализа t выборочное среднее и действующее значение монотонно убывают. Это означает, что когерентная составляющая, локализованная на частоте лунного прилива, отсутствует. Приведённые на рисунках 2 и 3 характерны для всех солнечных и лунных приливов на всех станциях наблюдения.

Для выявления некогерентных составляющих, локализованных па. частотах лунных приливов, в блоке 2 АСВиКС использовались ковариационные матрицы размера 1000 х 1000, построенные по траекторным матрицам анализируемых ВР. В блоке 4 АСВиКС СВ подвергались спектральному анализу с использованием стандартной процедуры быстрого преобразования Фурье (БПФ).6 Для каждого СВ вычислялся индекс когерентности (ИК), равный отношению амплитуды БПФ па. частоте прилива, к среднему значению амплитуды БПФ (аналог отношения «сигнал-шум»). При использовании БПФ для спектрального анализа ИК ограничен величиной M/2 (в данной работе — 500). Выявлялись все СВ, имеющие максимум амплитудного спектра па. частоте лунного прилива. Значения ИК для выявленных СВ приведены в последнем столбце таблицы 1.

Таблица 1. Действующие значения пекогерептпых некоррелированных компонент па частотах лунных приливов, определённые с использованием АСВиКС ( M = 1000, At = 1 час)

Прилив	Период,ч	Станция Воейково	Номер СВ 134	Действующее значение, В/м 0.74	! ИК 77.89
2N	14.3261	Верхнее Дуброво	130	0.63	16.33
		Душети	107	0.65	31.59
		ВлГУ	91	0.66	117
		Воейково	89	0.97	107
J 1	23.0646	Верхнее Дуброво	82	0.89	113
		Душети	119	0.63	57
		ВлГУ	61	1.02	157
		Воейково	80	1.03	147
M 1	24.8724	Верхнее Дуброво	77	0.92	134
		Душети	124	0.62	31
		ВлГУ	47	1.10	264
		Воейково	167	0.65	67
N 2	12.65	Верхнее Дуброво	135	0.62	59
		Душети	131	0.61	58
		ВлГУ	214	0.28	25.5
		Воейково	62	1.13	132
O 1, Q 1	25.8176, 25.71(6)	Верхнее Дуброво Душети	85 40	0.88 0.79	109 9
		ВлГУ	49	1.1	190
		Воейково	112	0.83	15
OO 1	18.9891	Верхнее Дуброво	101	0.77	32
		Душети	134	0.61	28
		ВлГУ	179	0.35	52.3

В таблице 1 приведены данные о СВ, имеющих максимумы спектра па. частотах лунных приливов. Приведены данные только об одном СВ, имеющем максимальное значение ИК для данных прилива, и станции. Для каждого такого СВ рассчитывалось действующее значение главной компоненты, равное произведению действующего значения ВР на А/орм\ Детально эта методика изложена в работе [12]. Как видно из таблицы 1, действующие значения составляющих Ez, спектрально локализованных па. частотах лунных приливов, лежат в интервале 0.6-1.1 В/м и хорошо согласуются для ВР, полученных па. различных станциях. В таблице 1 приведены только те лунные приливы, у которых частоты значительно отличаются от частот гравитациоппо-волпового воздействия двойных звёздных систем, анализу воздействия которых на. электромагнитное поле посвящена, следующая статья.

На. рисунках 4, 5, 6 приведены примеры собственных векторов и их нормированных к максимуму амплитудных спектров для некоторых лунных приливов и станций наблюдения. Как видно из рисунков, нормированные амплитудные спектры локализованы вблизи частот лунных приливов.

Показано [7], что если на вход АСВиКС воздействует полигармонический ВР, то СВ его ковариационной матрицы могут содержать гармонические составляющие только с теми частотами, которые содержатся в исходном полигармоническом ВР. Несмотря на то, что анализируемые нами BP Ez не являются полигармоническими, в СВ и их амплитудных спектрах, локализованных на частотах определенных приливов, следует ожидать наличие также и составляющих, локализованных на других частотах (в частности, на частотах других лунных приливов). Посмотрим с этой точки зрения на результаты, представленные на 4, 5, 6.

На рисунке 4 представлены СВ и его амплитудный спектр, имеющий максимум на частоте M1. Как отмечено ранее, дискрет частоты Af = 0.278 мкГц; наблюдаемая ширина амплитудного спектра не менее 4Af, в неё укладываются частоты приливов O1, Q1 и P1, K1. расположенные по отношению к частоте прилива M1 симметрично (см. рисунок 9). Именно это, на наш взгляд, обусловило правильную форму СВ, характерную для биений в случае близких частот, а также правильную форму амплитудного спектра СВ. На рисунке 5 слева от главного максимума амплитудного спектра СВ имеется пик, соответствующий частоте прилива 2N2 (с точи остью At). Таким образом, в отобранные для одного лунного прилива СВ могут вносить вклад не только другие лунные приливы, но и другие физические явления. Следовательно, оценки действующих значений, приведённые в 1 — это оценки сверху.

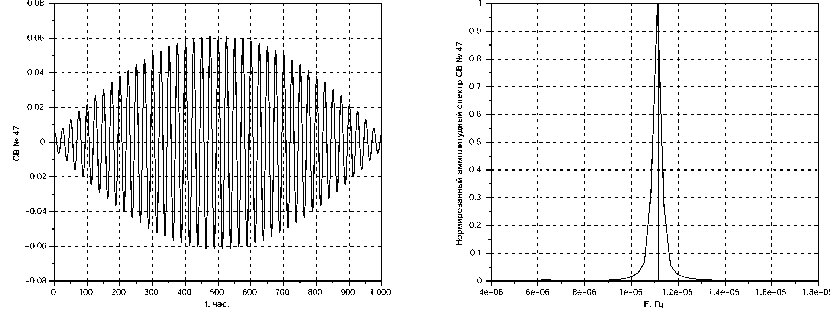
Рис. 4. Собственный вектор, локализованный на частоте лунного прилива М^ и его нормированный амплитудный спектр. Полигон ВлГУ. Сплошная вертикальная линия соответствует частоте прилива M1

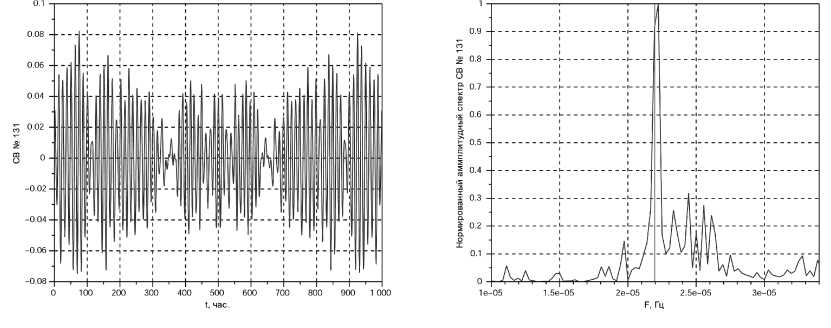
Рис. 5. Собственный вектор, локализованный на частоте лунного прилива N2, и его нормированный амплитудный спектр. Душети. Сплошная вертикальная линия соответствует частоте прилива N2

В [3] показано, что при амплитудных модуляциях одних локализованных по спектру составляющих ВР другими локализованными по спектру составляющими, АСВиКС должен выявлять СВ, АС которых локализован не только на частотах модулируемой и модулирующей составляющих, но и на суммарной и разностной частотах. С использованием АСВиКС такие составляющие были обнаружены; на рисунке 7 приводится пример трёх СВ, которые соответствуют частоте лунного прилива К₂, а также суммарной и разност ной частотам лунного прилива K2 и солнечного прилива

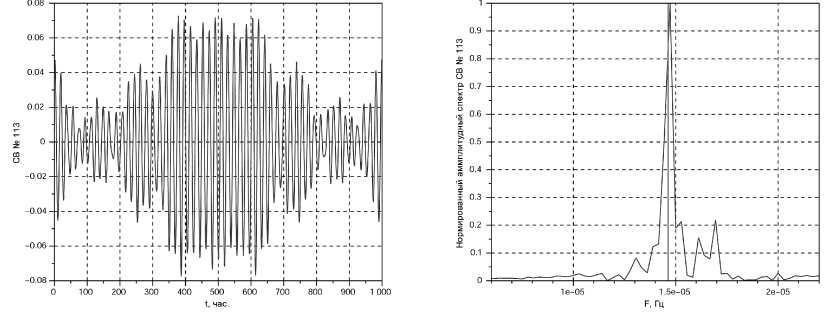
Рис. 6. Собственный вектор, локализованный на частоте лунного прилива OO1, и его нормированный амплитудный спектр. Воейково. Сплошная вертикальная линия соответствует частоте прилива OO1

S1. Предложенный подход для выявления взаимных модуляций эффективен, когда модулирующая частота заметно превышает спектральное разрешение БПФ, используемого при спектральном анализе СВ, что соответствует, при заданных параметрах АСВиКС, периоду модулирующей составляющей менее 1000 часов. Таким образом, для выявления годичных модуляций данный подход непригоден.

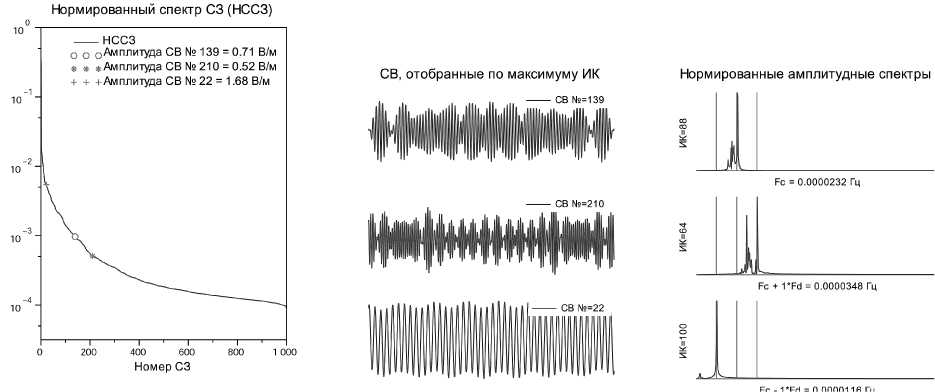
Рис. 7. Выявление СВ, спектрально локализованных на частотах лунного прилива K2, суммарной и разностной частотах лунного прилива K2 и солнечно го прилива S1 по данным станции наблюдения Воейково. Левый график — НССЗ с нанесёнными на него нормированными СЗ для выявленных СВ, в легенде графика указываются действующие значения выявляемых компонент. Три средние графика соответствуют выявленным СВ для частот, равных частоте лунного прилива K2, суммарной и разностной частоте соответственно. Справа — три графика АС для соответствующих СВ. Вертикальными линиями на этих графиках показаны выявляемые частоты.

Показано, что амплитуды составляющих, локализованных на частотах лунных приливов, изменяются периодически с частотами, кратными 1 г од^-1. Для этого нормы проекций ВР на спектрально локализованные на частотах лунных приливов СВ сравнивались с тестовым полигармони-ческим рядом, составляющие которого имеют единичные амплитуды и частоты, кратные 1 г од^-1. На рисунке 8 приведен пример амплитудного спектра для нормы проекции ВР наблюдений на станции Душети на СВ, локализованные на частоте лунного прилива O1.

Обнаружение АМ подтверждает влияние изменения положения Земли относительно Солнца в течение годового цикла на составляющие ВР Ez, локализованные на частотах лунных приливов. Следует отметить, что такие модуляции характерны для большинства СВ ВР Ez, что свидетельствует о том, что порождающие их физические процессы также подвержены влиянию годичных циклов.

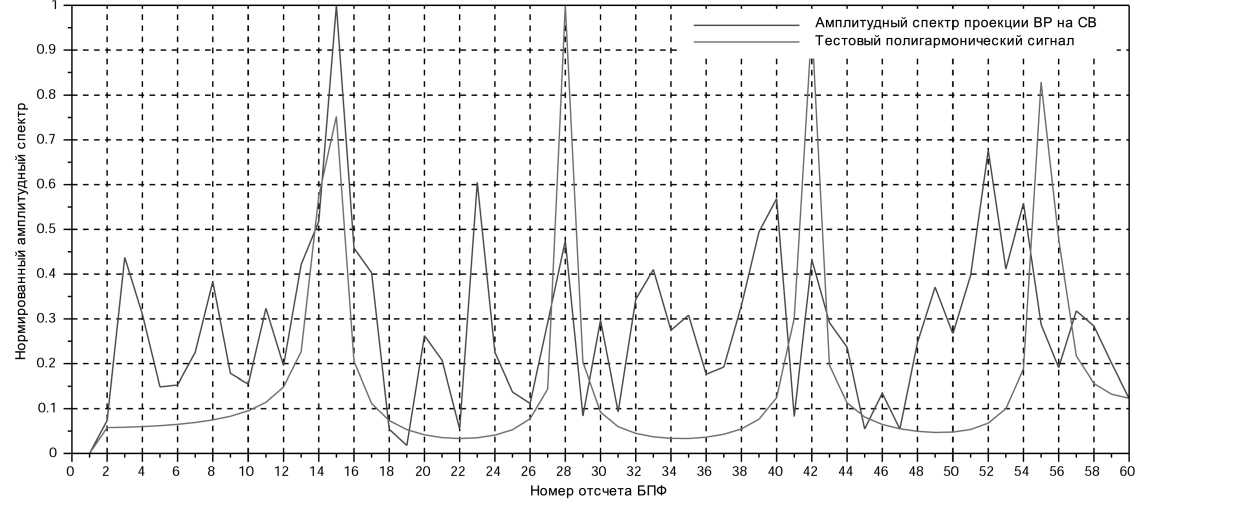
Рис. 8. Амплитудный спектр нормы проекции BP Ez на станции Душети на подпространство,образованное СВ №40 и №43, спектрально локализованные на частоте лунного прилива O1, в сравнении с амплитудным спектром тестового полигармонического ВР с периодами составляющих 1, 1/2, 1/3, 1/4 года

Естественно задаться вопросом: не могут ли собственные векторы, локализованные на частотах лунных приливов, возникать случайно? Таким образом, задача подтверждения или опровержения гипотезы случайности приобретает особое значение. Воспользуемся стандартными подходами [8] для оценки вероятности «ложной тревоги» (вероятности того, что гипотеза случайности верна). Известно, что такая вероятность определяется, с одной стороны, правилом принятия решения, а с другой — статистическими свойствами используемых в этом правиле величин. В качестве решающего правила можно использовать простейшее правило выборочного контроля «к из К». Сформулируем это правило.

Правило 1 Пусть имеется К значений ИК Ij /1 <  j <  К), полученных для СВ, отобранных при анализе всех имеющихся BP Ez для всех исследованных час тот лунных приливов. Если к ^ к₀ из этих значений превышают соответствующие им пороговые значения hj, то гипотеза случайности отвергается.

Для правила 1 гипотеза случайности приобретает вид

Гипотеза 1 Наблюдаемые к ^ к₀ из К возмоснсных превышений порога hj индексами когерентности Ij возникли случайно.

Эта гипотеза имеет простую альтернативу

Гипотеза 2 Наблюдаемые к ^ к₀ из К возмоснсных превышений порога hj индексами когерентности Ij обусловлены не случаем.

Примем в качестве hj квантили, соответствующие вероятности их превышения индексом когерентности Ij, равной р. Тогда вероятность того, что гипотеза 1 верна (вероятность «ложной тревоги») в рамках биномиального распределения оценивается соотношением

K

P„ _T(kg , К, h) = P {к > ко | Гипотеза 1} = ^ CK p^k (1 - p)^K-k,             (0.6)

где p — вероятность превышения величиной ИК порога hj.

При hj, равных медиане И К, что соответствует р = 1/2, и ко >  рК соотношение (0.6) упрощается и приобретает вид неравенства

C^{k 0}

Р_лт(ко,К) ^ 2^ (К - ко + 1).                            (0.7)

Этому соответствует простое решающее правило

Правило 2 Если наблюдаются не менее к₀ (из K возможных) значений ИК, превышающих медианное значение ИК, то принимается гипотеза, альтернативная гипотезе 1.

Для использования правила 2 и оценки Рлт формулой (0.7), необходимо оценить медианные значения ИК на частотах лунных приливов. С этой целью были проведены два вычислительных эксперимента.

В первом из вычислительных экспериментов из всех четырёх исходных ВР строился ансамбль отрезков ВР длины N = 104 отсчётов (объём ансамбля 50 60). Для каждого такого отрезка строились ковариационные матрицы, вычислялись СВ и их БПФ. Для каждого из вычисленных БПФ определялось положение максимума амплитудного спектра и ИК. Далее для каждого положения максимума амплитудного спектра была построена выборка ИК, а затем по этой выборке оценивалась медиана. Таким образом была построена зависимость медианы ИК от частоты максимума амплитудного спектра СВ, характеризующая все имеющиеся экспериментальные ВР. Эта зависимость приведена на рисунке 9.

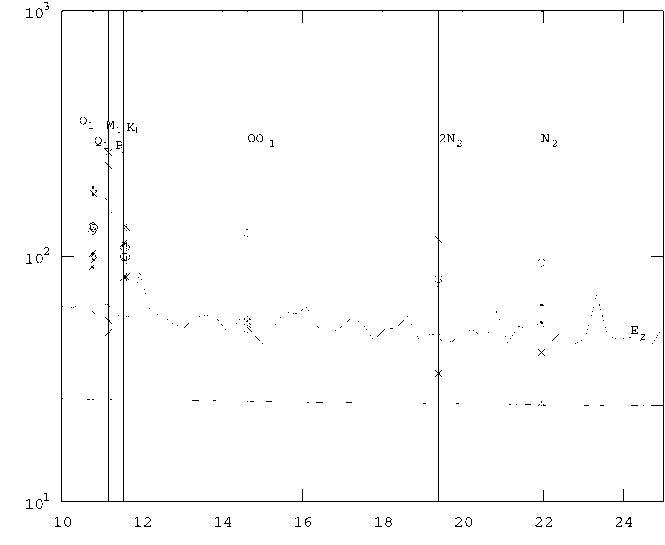
Рис. 9. Зависимость ИК от положения максимума амплитудного спектра СВ, полученная вычислительным экспериментом для отрезков ВР Ez (верхняя кривая) и отрезков БГШ той же длины (нижняя кривая), в сравнении с ИК СВ ВР Ez, спектрально локализованных на частотах лунных приливов: вертикальные линии — частоты лунных приливов; х — ВлГУ; * — Душети; о — Воейково

Аналогично, во втором вычислительном эксперименте была определена зависимость медианы ИК от частоты максимума амплитудного спектра СВ для ансамбля отрезков ВР белого гауссовского шума (БГШ), имеющих длину N = 104 отсчётов (объём ансамбля 200). Эта зависимость также приведена на рисунке 9. Как видно из рисунка 9, медианные значения ИК для БГШ существенно меньше медианы ИК для ВР Ez.

Использование соотношения (0.7), данных об ИК СВ, локализованных на частотах лунных приливов, а также оценок медианных значений, полученных в первом вычислительном эксперименте, позволяет получить оценку для k₀ = 36, K = 45 в виде не равенства Р_{л т}(36,45) < 2-5 • 10-4.

Второй вычислительный эксперимент не имеет непосредственного отношения к анализируемым ВР. Однако он позволяет ответить на нередко слышимое от критиков утверждение: «Возьмите гауссовский шум, и Ваш АСВиКС даст тот же результат, который Вы наблюдаете при анализе ВР Ez». Вычислительный эксперимент показывает, что при действии БГШ на АСВиКС наблюдаемое превышение значений ИК может возникнуть с вероятностью Р_лт (43,45) < 8.4 • 10^-11.

Таким образом, анализ временных рядов многолетних наблюдений Ez на четырёх станциях (Воейково, Душети, Верхнее Дуброво, Полигон ВлГУ) с использованием анализатора собствен- пых векторов и компонент сигнала позволяет говорить о выявлении иекогереитпых сложнопериодических составляющих па. частотах лунных приливов с вероятностью «ложной тревоги», не превышающей 2.5 • 10—4.

Для получения результатов работы были использованы авторские методики и программное обеспечение, предоставленные ООО «БизпесСофтСервис» [13,14].

Заключение

• 1.    Показано, что компоненты временных рядов (ВР) вертикальной составляющей электрического поля ( Ez) в пограничном слое атмосферы Земли, локализованные на частотах лунных приливов, в отличие от солнечных приливов некогерентны. Это приводит к тому, что с увеличением интервала, анализа спектральные оценки, полученные с помощью классической квадратурной схемы, уменьшаются; таким образом, с использованием квадратурной схемы составляющие, локализованные на. частотах лунных приливов, ненаблюдаемы.

• 2.    Анализатор собственных векторов и компонент сигнала [3] (АСВиКС), в отличие от классической квадратурной схемы спектрального анализа, позволяет выявлять некогерентные составляющие, локализованные на. частотах лунных приливов. АСВиКС использует представление ВР в ортонормированием адаптивном базисе собственных векторов 1 (СВ) ковариационной матрицы ВР. СВ полностью определяются ковариационной матрицей и, следовательно, несут в себе информацию о внутренних связях ВР на. выбранном интервале анализа. В данной работе интервал анализа имеет длину M = 103 отсчётов ВР при времени дискретизации 1 час. Как показали исследования ВР Ez, СВ имеют сложнопериодическую структуру. Спектральный анализ СВ позволяет выявить среди них те, которые локализованы на. характерных для ВР частотах.

• 3.    Каждому СВ 1 соответствует собственное значение Ai (СЗ), величина которого равна средней на интервале анализа энергии составляющей ВР, соответствующей СВ. СЗ Ai, отнесенные к их сумме и упорядоченные по убыванию, образуют нормированный спектр СЗ (НССЗ). В этому случае нумерация СВ ведётся по убыванию соответствующих им СЗ. Значения А“^орм' НССЗ определяют относительный энергетический вклад соответствующих СВ 1i некоррелированных составляющих в исследуемом ВР. Действующее значение составляющей в этом случае определяется как произведение действующего значения ВР на ^А”^орму Показано, что действующие значения составляющих, локализованных па. частотах лунных приливов, лежат в интервале 0.6-1.1 В/м.

• 4.    Степень локализации амплитудных спектров СВ вблизи частот лунных приливов оценивалась индексом когерентности (ИК), величина, которого равна отношению амплитуды быстрого преобразования Фурье (БПФ) па. частоте прилива, к среднему значению амплитуды БПФ. ИК можно рассматривать в качестве аналога отношения «сигиал-шум»; его величина, ограничена величиной M/2 (в данной работе — 500). Для исследованных ВР и частот лунных приливов экспериментальные оценки ИК лежат в интервале 9-264.

• 5.    На основании вычислительного эксперимента с использованием ВР Ez построена зависимость медианы ИК от частоты максимума, амплитудного спектра СВ. Для максимумов амплитудных спектров, соответствующих частотам лунных приливов, медиана. ИК лежит в интервале 47-60. Аналогично с использованием вычислительного эксперимента определена зависимость медианы ИК от частоты максимума, амплитудного спектра СВ для ансамбля отрезков ВР белого гауссовского шума. (БГШ). Следует отметить, что медианные значения ИК для БГШ меньше, чем у отрезков наблюдаемых ВР.

• 6.    Сравнение конкретных значений ИК, полученных для ВР Ez и исследованных частот лунных приливов, с медианными значениями ИК, позволяет с использованием биномиального распределения оцепить вероятность «ложной тревоги» (вероятность случайного превышения медианы конкретными значениями ИК). Для частот лунных приливов 36 из 43 конкретных значений ИК превышают медиану, чему соответствует вероятность «ложной тревоги» не более 2.5 • 10^-4.

• 7.    Показано, что амплитуды составляющих, локализованных на. частотах лунных приливов, как и большинства других некоррелированных составляющих, изменяются периодически с частотами, кратными 1 г од^-1.

Таким образом, использование АСВиКС с высокой достоверностью подтверждает наличие некогерентных сложнопериодических компонент вертикальной составляющей Ez электрического поля Земли, спектрально локализованных па. частотах лунных приливов, позволяет оцепить степень их когерентности и их действующие значения.

Использованные сокращения

АСВиКС анализатор собственных векторов и компонент сигнала

БГШ белый гауссовский шум

БПФ быстрое преобразование Фурье

ВР    временной ряд

ИК    индекс когерентности

НССЗ нормированный спектр собственных значений

СВ     собственный вектор

СЗ     собственное значение

ССЗ спектр собственных значений