Выпрямление тока, индуцированного в сверхрешетке совместным влиянием двух электромагнитных волн

ВЫПРЯМЛЕНИЕ ТОКА, ИНДУЦИРОВАННОГО В СВЕРХРЕШЕТКЕ СОВМЕСТНЫМ ВЛИЯНИЕМ ДВУХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН *

Д.В. Завьялов, С.В. Крючков, Е.И. Кухарь

Исследовано совместное влияние двух электромагнитных волн (синусоидальной и кноидальной) на электропроводность полупроводниковой сверхрешетки. Показана возможность взаимного выпрямления волн, так что в плотности индуцированного тока появляется постоянная составляющая. Дано качественное объяснение обнаруженного эффекта. Приведены конкретные вычисления для случая, когда частота синусоидальной волны в два раза больше частоты кноидальной. Сделаны численные оценки.

В настоящее время в лазерной физике особое внимание уделяется изучению нелинейных электромагнитных волн. Это связано с достижениями в области создания потоков мощного электромагнитного излучения [1]. Высокая интенсивность лазерного излучения приводит к отклонению формы электромагнитной волны, распространяющейся в СР, от синусоидального вида. В [2]—[4] изучались эффекты взаимного выпрямления электромагнитных волн применительно к различным механизмам нелинейности среды распространения волн. Эффект взаимного выпрямления в СР двух синусоидальных электромагнитных волн, частота одной из которых вдвое больше, чем у другой, изучен в [4]. Однако считать синусоидальными волны, распространяющиеся в СР и имеющие большие интенсивности, было бы слишком грубым приближением. В [5] показано, что в случае, когда столкновения с нерегулярностями кристаллической решетки достаточно редкие, так что v «pl (v — частота столкновений, ю_р1 — обобщенная плазменная частота электрона в минизоне), уравнение д’Аламбера, записанное для СР, перейдет в уравнение sine-Gordon. Последнее в качестве общего периодического решения имеет эллиптические функции Якоби [6]. То есть форма электромагнитной волны, распространяющейся в СР, будет кноидальной. Поэтому представляет интерес рассмотреть взаимное выпрямление электромагнитных волн в СР в случае, когда хотя бы одна из волн является интенсивной и имеет кнои-дальную форму.

Пусть в направлении оси СР приложено электромагнитное поле двух волн, одна из которых представляет собой слабую синусоидальную волну с частотой со, а другая — кноидальную волну.

Задача состоит в нахождении постоянной составляющей плотности тока, возникающего под действием поля электромагнитных волн. Считаем, что выполняются условия:

edE_x « А, йО₀ «А (А — ширина минизоны), позволяющие решать задачу квазиклассически [7]. Зависимость плотности тока от времени находится по формуле, полученной с использованием уравнения Больцмана в приближении постоянной частоты столкновений v.

Л(0=

4ле

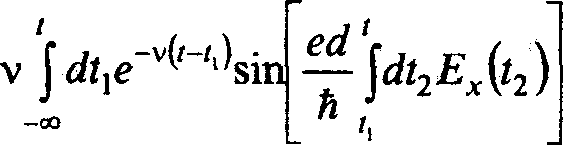
Здесь поле Е^О есть сумма полей двух рассматриваемых волн:

Е_х (z) = Е_гсо^ю Z+ф)+■

^cnfOgZ, к], 0 < к < 1; Е_х Jh[kQ₀Z, к^-1 ], к > 1,

где

edE. к =----

2ЙП0

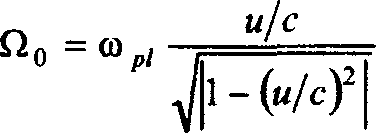
сп[х, к] и dn[x, к]

— модуль нелинейности;

— параметр размерности частоты;

— эллиптические функции Якоби [6].

Будем считать, что выполняется условие Е2 « —- позволяющее считать синусоидальную ed волну слабой. Постоянная составляющая тока (1) находится как среднее значение плотности тока по времени в линейном приближении по амплитуде синусоидальной волны Ет

В случае 0 < к < 1 получается следующее выражение для постоянной составляющей плотности тока:

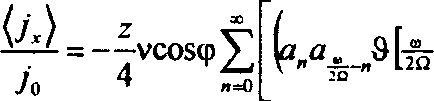
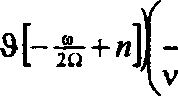
2nd-и

+ (2лП-о)2

2nd ) v2+(2nd)2^

/  2nQ+® 2nQ

2n \v2+(2«q+®)2 v2+(2mQ)2,

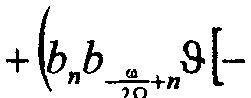
& + пУь^^^ fe- (и +1)]

(2n + l)f2-(0

+ ((2h + 1)Q-©)2

(2h + 1)Q v²+((2n + l)Q)\

ю /   (2n + l)Q+co (2n + l)Q

2n \v2 + ((2n + l)fi -ко )2 v2 + ((2n + l)fi)2,

Здесь ^H~

■ _^Ё_ 7о 4ле^ ’

_ edE2

2 - ""^ — безразмерная амп- литуда синусоидальной волны.

.        . л² q"

U° К^ ’ °"  K^l-q?’

2 п*т я_к²

Л

Q = Q0— °2^(к)‘

Як ^=ехР

лК'(к)'

^(k)J

Наличие функции 0 в (3) показывает, что постоянная составляющая появляется при таких значениях параметра к, при которых частота кноидал ьной волны в четное число раз меньше частоты синусоидальной волны. Поэтому зависимость (j,) от к-имеет вид чередующихся пиков (рис. 1).

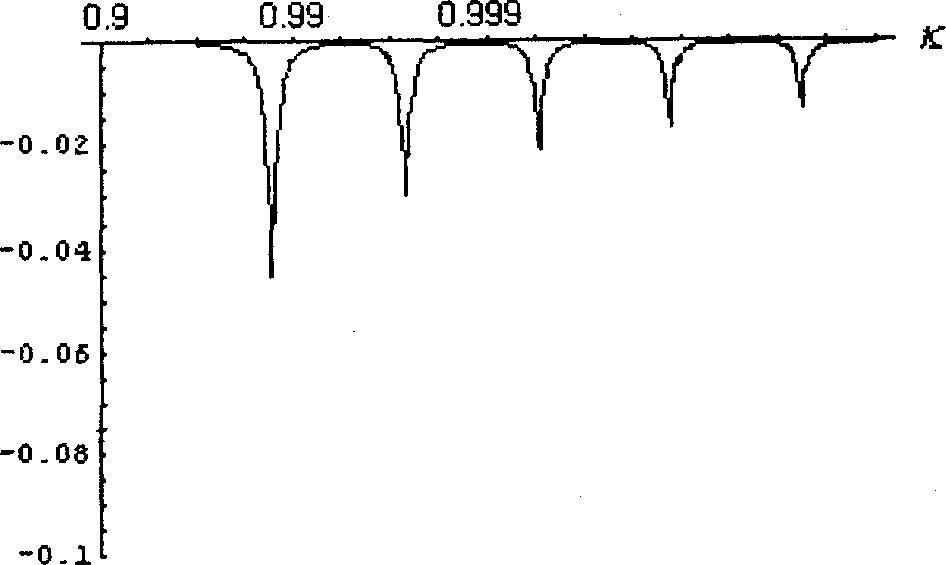
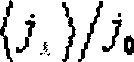
Рис. 1: z = 0,2; Q_ot = 5; сот = 10; ф = 0

Реальное уширение пиков должно быть обусловлено немонохроматичностью слабой волны, которая при расчетах предполагалась строго монохроматичной.

Такой характер выпрямления обусловлен нелинейной зависимостью тока от потенциала поля, которая, в свою очередь, обусловлена непараболичностью закона дисперсии носителей тока в минизоне. Нелинейность зависимости тока от потенциала приводит к амплитудной модуляции колебаний тока: максимальное значение плотности тока начинает зависеть периодически от времени. При определенном соотношении частот осцилляций тока и колебаний максимального значения тока возможна следующая ситуация. В тот промежуток времени, когда ток течет в некотором направлении оси Ох, его максимальное значение больше максимального значения осцилляций этого тока, в тот период времени, когда направление тока вследствие его колебаний имеет противоположный знак. Это означает появление постоянной составляющей электрического тока. Направление этого тока, очевидно, должно зависеть от начальной фазы синусоидальной электромагнитной волны. Как видно из формулы (3), направление тока меняется на противоположное, если фаза синусоидальной волны изменяется на л.

Пусть условие <у = 2Q выполняется при некотором значении параметра нелинейности к= к_е, тогда выражение для плотности тока (при Q_ot »1) будет иметь вид:

^) =

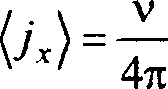
8л-2

К’М

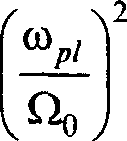
-E^Ko^osp,

(2ЕМ-КИ)^ ?'2

2л 1-^

2(l + qJ

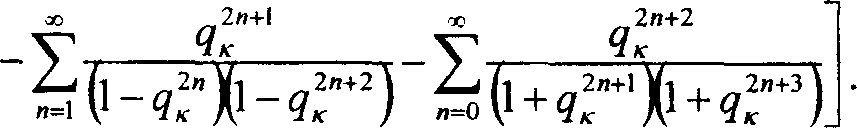
Значение к^ удовлетворяет равенству

К(к^=л^-. го

В случае /с «1 8(к^~к², так что ^~ Е²Е_гсо&ф, как в случае «теплых» электронов в однородном полупроводнике [3].

В случае к> 1 постоянная составляющая плотности тока имеет вид:

/о

(Ю)

где

A^-v^aX

Л=1

2иП* v² +{2п£1*У ’

(Н)

S(k-) = — vcos^

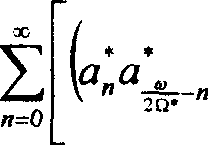
-Aij+a’a^Sl-^ + nl

2«Q’ - го

+ (2wQ* -zy)2

2nQ*

v² + (2яО*)²_/

. .           { 2mQ* + to

-«п^+л^ + и| ——7—--;

2“"         \v2 + (2nQ + to

2«Q* v² +(2nQ*)²_?

+ (^L^l" 2«r + «]- 6>L ⁴      2Q*                             20*

। 2yQ* - to         2mQ*

\v² + (2nO* - to)² v¹ + (ini

1 2nQ*+to 2nQ*

-^-S-Ki^UiF + ИJ ~2  /- „• V 2

^2O*        \v²+(2mQ + mj v²+(lni

Здесь

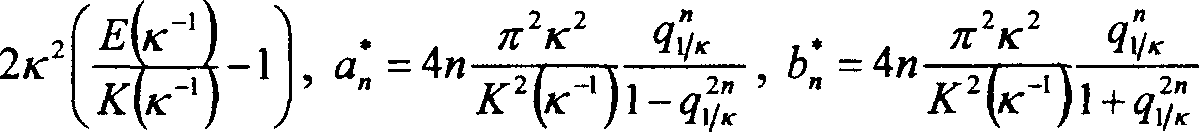
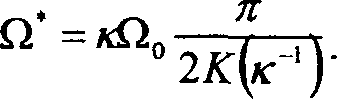
Первое слагаемое в (10), равное Л(к), не зависит от параметров синусоидальной волны. Оно отвечает току, возникающему из-за наличия постоянной составляющей напряженности поля кноидальной волны £1с?и[к£20г, к-1]. Этот ток не связан с эффектом взаимного выпрямления и возникает при наличии одной кноидальной волны. На кривую зависимости Л(к) (рис. 2) накладываются пики, связанные с наличием синусоидальной волны (рис. 3). «Всплески» тока возникают тогда, когда частота кноидальной волны, вычисляемая по формуле (14), в четное число раз меньше частоты синусоидальной волны.

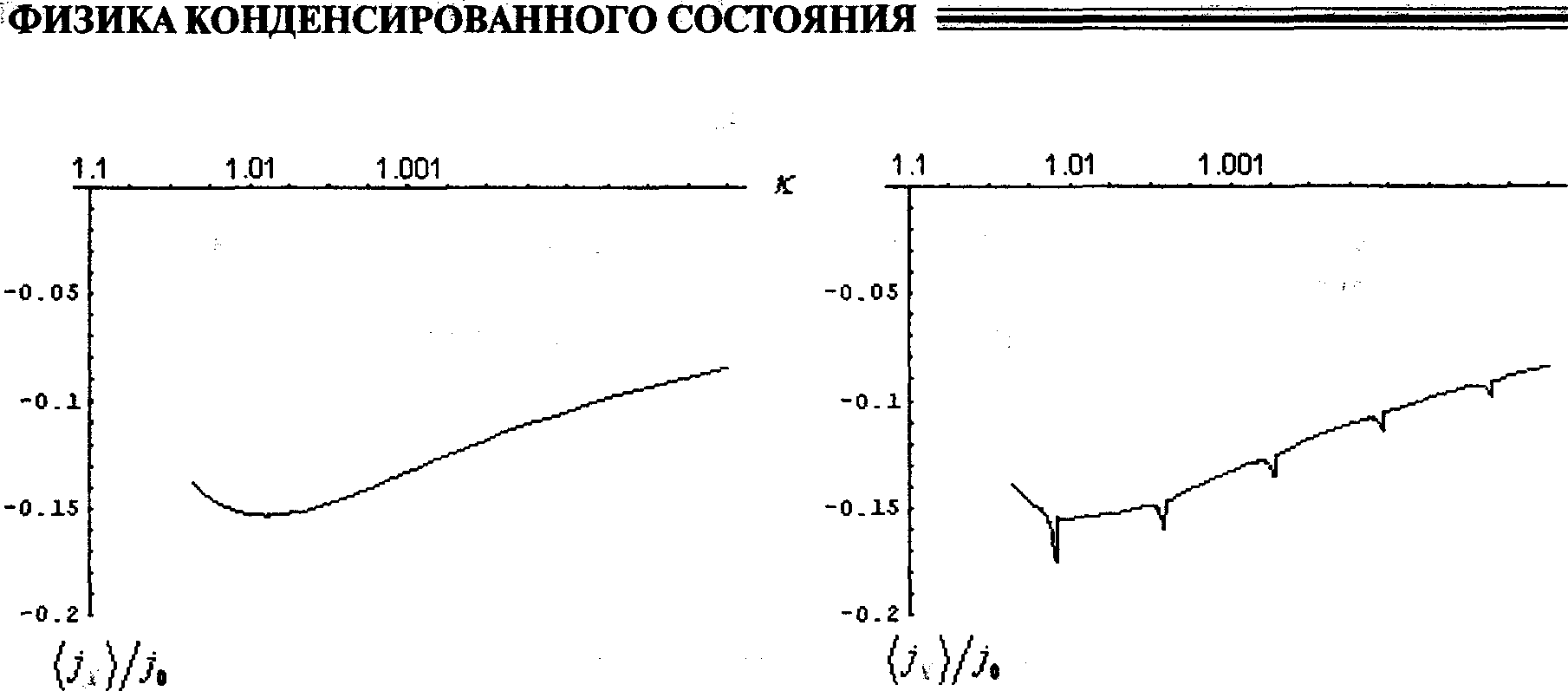
Рис. 2: z = О                            Рис. 3: z = 0,2; Пот = 5; сот = 10; ф = 0

Пусть условие о = 2Q* выполняется при некотором значении к^, тогда выражение для плотности тока (при Q_or »1) будет иметь вид:

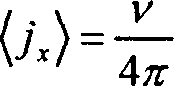
1^0 J

р(к_о)+ Е₂ R(k₀ )cos ф ed

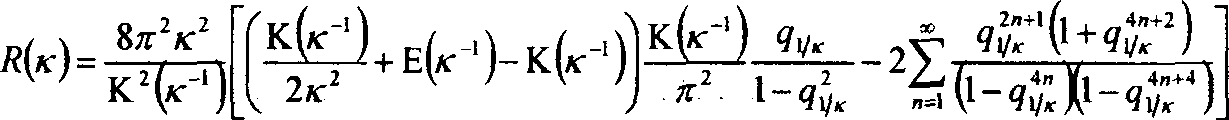
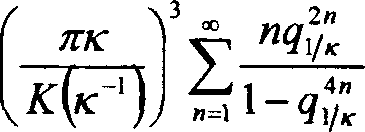
Значение к^ удовлетворяет равенству

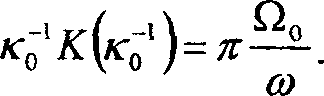
Если частоту <о менять от опыта к опыту, то будет меняться и значение к^, удовлетворяющее условию максимума (9) или (18). При этом зависимость тока от частоты со будет определяться видом функций 5(к), R(k) и Р^к). Эти функции исследованы нами на ЭВМ и представлены на рисунках 4 и 5.

Численные оценки при следующих параметрах щ_р| * 10¹²с', d ~10^ см, ty^lO^c¹ дают следующие значения токов: 7₀ «10² А/см² , j_max «0.05 j₀ — первый максимум при 0<к<1, Утах * 0-2У_о — последний максимум при 0 <  к < 1 ■

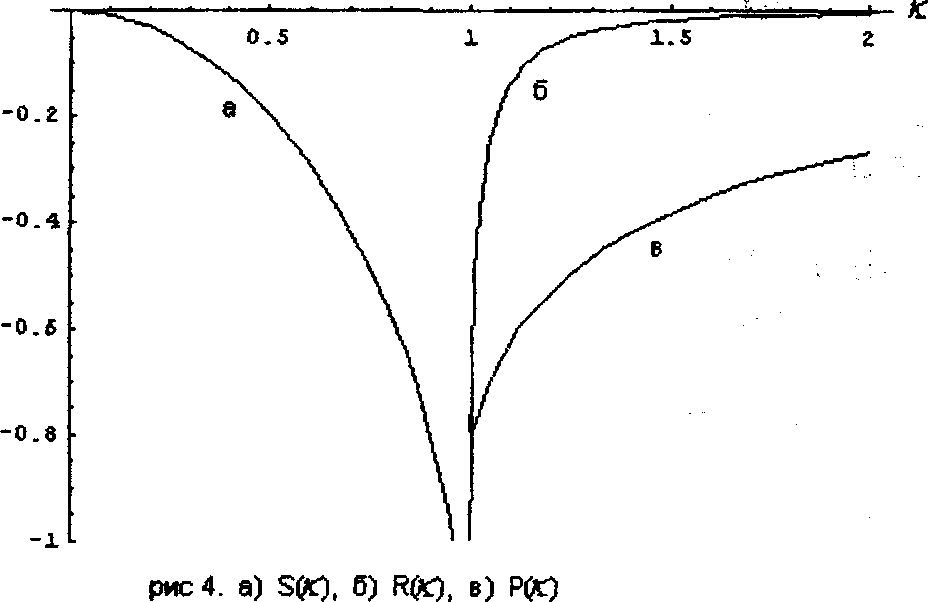
Рис. 4: а) ЭД; б) ЛЮ; в) ЛЮ

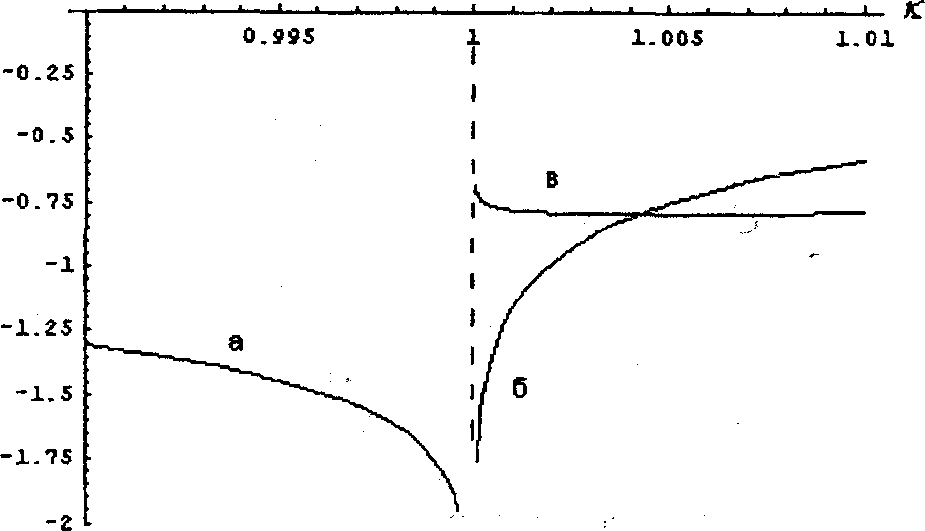
рис 5. а) ЭХ), б) RiX), В) РХ)

Рис. 5: а) ЭД; б) ЛЮ; в) ЛЮ

Результаты могут быть использованы, например, для изучения формы кноидальной волны, распространяющейся в СР. Допустим, что вдоль слоев СР распространяются синусоидальная волна известной частоты о и кноидальная волна с неизвестным параметром Q_o. Будем изменять амплитуду этой волны до тех пор, пока в СР не появится постоянная составляющая тока. Если известно значение амплитуды к^ кноидальной волны, при которой ток достиг своего максимума, то Q_o находится из условия максимума тока в СР (9) или (18).