Вывод тяжелой материальной точки на базовую траекторию при наличии геометрических ограничений на дополнительные управления

Данная статья продолжает цикл исследований, представленный в работах [3–6]. Решается задача коррекции управляемого полета точки, движущейся в однородном поле тяжести и испытывающей сопротивление среды, пропорциональное квадрату скорости. Начальные условия полета точки заданы приблизительно. Их точные значения становятся известными только в момент старта. В связи с этим базовый закон управления точкой, реализующий базовый закон движения точки (т.е. отвечающий вероятным начальным условиям) требует коррекции.

Коррекция осуществляется путем введения дополнительного управления, которое входит в дифференциальные уравнения движения точки аддитивно базовому управлению. Закон изменения дополнительного управления определяется из условия обраще- ния в ноль фазового вектора некоторого управляемого линейного объекта, динамика которого описывается дифференциальными уравнениями движения точки, линеаризованными в окрестности пары "базовое управление, базовое движение". При наличии геометрических ограничений на дополнительное управление задача обнуления фазового вектора линейного объекта в заданный момент времени может оказаться неразрешимой. Для этого случая в работе [6] она была заменена задачей минимизации нормы фазового вектора линейного объекта и успешно решена.

В данной статье предполагается, что начало координат принадлежит области достижимости линейного динамического объекта для заданного момента времени.

С одной стороны это предположение позволяет с любой степенью точности приблизить норму фазового вектора линейного объекта к нулю.

С другой стороны факт принадлежности начала координат области достижимости делает невозможным применение процедуры построения оптимального управления из работы [6]. В настоящей статье приводится алгоритм управления линейным объектом, разрешающий это противоречие, а также ставится и решается задача быстродействия по приведению фазового вектора линейного объекта в начало координат.

1. Уравнения движения управляемой точки и линейный динамический объект

В работе [4] были выведены дифференциальные уравнения управляемого полета тяжелой материальной точки в однородном поле тяжести в среде с сопротивлением, пропорциональным квадрату скорости ( рис. 1).

x =--x • ^x2 + y2 + z2 + v, mm k        2     22

y =—y• Vх + y + z 4—v2,(1)

mm k  2221

z = — Z ’ у x + y + Z — g 4— v, mm

Выпишем дифференциальные уравнения линейного управляемого динамического объекта q = A (t) q + B (t) u . (2)

Здесь
	" 0	0	0	1	0		0 "
	0	0	0	0	1		0
	0	0	0	0	0		i
	0	0	0	d F	d F	d F
A ( t ) =				d x	d y	д		,
	0	0	0	d F	_  d F 2	dF 2
				d x	d y	d z
				d F	d F	;  dF
	0 V	0	0	d x	d y	d z J		x = x ( t ) , y = y ( t ) . z = z ( t )
		< 0	0	0 Л		[q?
		0	0	0		q 2
B ( t ) =		0 1 m	0 0	0 0	, q =	q 3 q 4	e R	6,
		0	1 m	0		q 5
		V 0	0	1 m J		V q 6 J

F i ( x , y , Z, V i ) = — — x • 7 x ² + y ² + Z ², m

F ( x , y , z , v ₂ ) =— — y •   x ² + y ² + z ²,

m

F ( x , y , z , v ₃ ) = —z • ^x ² + y ² + z ², m

u u = u2

e P =

V ^u 3 J

где z — вертикальная, x , y — горизонтальные координаты точки, m — ее масса, g — ускорение силы тяжести, k = const — коэффици-

|u_t | <  a_t, i = 1,2,3 > о R³

—

ент пропорциональности, а

v ₁

дополнительное управление точкой,

v ₂

e R³

век-

x = x (t), y = y (t), z = z (t), t e[ 10, T ] —

v

базовый закон движения точки.

тор управляющих параметров.

2. Наведение фазового вектора линейного динамического объекта на начало координат

Символом П[t0, T] обозначим множество всех допустимых программных управлений, удовлетворяющих условию u (t )g P, t g[ t^, T ].

Символом q 0 = q (', t 0, q 0, u (0)

обозначим движение линейного динамического объекта (2), выходящего из начального положения ( t ₀, q ₀) и порожденного программным управлением и ( • ) g П [ t ₀, T ] . Поставим задачу о наведения фазового вектора линейного динамического объекта на начало координат в момент времени t_x g [ t ₀, T ] .

Задача 1. Определить программное управление

и0 (^П[ 10, ti ]

такое, что

J q ( t i , t 0 , q 0 , u ⁰ ( • ))! = _umin^ || q ( t_x,t 0 , q 0 , u ( • ))| .

Решение задачи 1 основывается на двух утверждениях [1–2].

Лемма 1. Пусть г° ( t ₀, q_Q , t_x ) >  0 . Тогда максимум в равенстве (3) достигается на единственном векторе l ⁰ .

Теорема 1. Пусть г° ( t ₀, q ₀, t^ ) > 0 . То

гда программное управление ue (•), решающее задачу 1, удовлетворяет равенству

Uи^е ( t ) , Q [ t_x , t ] ^Тр l °) = mn( u , Q [ t_x , t ] ^Тр l °),

t ^{g [} t 0 , t i ^] .

В статье [6] приведен подробный алгоритм, реализующий решение задачи 1.

Во втором случае

£Q

⁽ t 0 , ^q 0 , t i )

min u Оп[ t 0, ti ]

||^{q (} t i , t 0 , ^q 0 , ^u ( • ⁾⁾||

= 0 .

Тогда условия леммы 1 и теоремы 1 не выполнены и указанный выше алгоритм решения задачи 1 не работает.

Программное управление, разрешающее задачу 1, в этом случае ищется в виде

u0 (t ) = <

0, t g [ 1 0 , t * ) , _ч u^e ( t ) ,     t g [ t * , t i ] .

Определение 1. Множество

G ( t 0 , q 0 , t i ) =

= { q = q ( t i , 1 0 , X 0 , и ( - ) )| и С) еП [ 1 0 , t i ] } c R⁶ называется областью достижимости управляемого линейного динамического объекта в момент времени t для начального положения { t 0 , q 0 } .

Точка 0 g R ⁶ (начало координат) может

Здесь момент времени t определяется из условия г ⁰ ( t , , q ( t * , 1 ₀, q ₀,0 ) , t _i ) > 0 , а программное управление u^e ( t ) , t g [ t* , t_x ] стро-

не принадлежать, а может и принадлежать области достижимости.

В первом случае

г

⁽ t 0 , ^q 0 , t i )

min u Оп[ t 0, ti ]

||^{q (} t i , t 0 , ^q 0 , ^u ( • ⁾⁾||

> 0 .

При этом [1–2]

г° (t0, q0, t ) = max v 0  70 u      ||z||=i

^^q 0 , Q [ t i , t 0 ^{] l} ^ +

t ₁

t ₁

+

Jmn uu , ⁽ Q ^[ t^ r ] B ) Тр fyr ,

t ₀

где Q [ t , т ] , t , т g [ t ₀, t_x ] - фундаментальная

ится в соответствие с алгоритмом, указанным в первом случае, для начального положения ⁽ t * , ^{q (} t * , t 0 , ^q 0 ,⁰ ) ) .

Условия леммы 1 и теоремы 1 выполнены и такой способ определения разрешающего программного управления корректен.

В силу непрерывной зависимости величины г ° ( t* , q ( t* , t ₀, q_Q ,0 ) , t_x ) от момента времени t его всегда можно подобрать так, чтобы имело место двойное неравенство

0 <  £ ⁰( t * , q ( t * , 1 0 , q 0 ,0 ) , t i ) < J , (4) где 5 — параметр точности. Заметим, что если условие (4) не выполняется для всех t * ^g ( t 0 , t i ] , то

0 = г ⁰ ( t i , q ( t i , 1 0 , q _o,0 ) , t i ) ^

^{q (} t _i, t 0 , ^q ₀,⁰ ) ⁰ ,

матрица Коши для однородного уравнения q = A ( t ) q .

и        программное        управление u0 (t) = 0, t g[t0, tj ] решает задачу 1.

Для случая e ⁰ ( t₀ , q ₀, t_{ ) = 0 поставим и решим задачу быстродействия по приведению фазового вектора линейного объекта в начало координат.

Задача 2. Определить наименьший момент времени t *e [ t^ , t_x ] и программное управление u *(- ) еП^ t ₀, t * J , удовлетворяющие условию q ( t * , t ₀, q ₀, u *( • ) ) = 0 .

Решение задачи 2 начинается с определения момента времени t *e[ t0, tr ] как наименьшего корня уравнения max

с

q 10 = -40 м, q 20 = 20 м, q 30 = -11.4762 м q 40 = 10 м/сек, q 50 = 20 м/сек, q 60 = -20,5954 м/сек.

Принятые числовые данные совпадают соответствующими данными из работы [6].

Из той же работы берутся базовое программное управление точкой и ее базовый закон движения.

В данной статье принимается ^ = 0.1 м 0.1 м, ^ = 0.3 м a = 2500 н, a2 = 2500 н, a3 = 2050 н.

Непосредственно проверяется, что

0 e G ( 1 0 , q₀, t i ) ^ e ⁰ ( 1 0 , q ₀, t i ) = 0 .

t *

т

= 0 .

t 0                                                       _

Далее строится монотонно возрастающая последовательность

T1,---,Tk,...^t*-0   Tk e[10,t’), сходящаяся слева к моменту времени t*. Номер k выбирается из условия

⁰ <  ^{e (} t 0 , ^q 0 ,^T k ^{) —} &  .

Для момента времени T_k выполнены условия леммы 1 и теоремы 1 , поэтому для него корректно применить алгоритм построе-

При решении задачи 1 было установлено t* = 0.75 сек ,

0 <  e ( t , , q ( t , , 1 0 , q 0 ,0 ) , t 1 ) = 0.0326 <  0.1 = ^ 1 и построено программное управление

u ⁰ ( t ) = <

0,       t e [ 1 0 , t , ) ,

^ u^e ( t ) ,     t e [ t , , t 1 ] ,

ния разрешающей программной ue (t), t e [t0,т] для начальных

{ t 0 , q 0 } •

Управление u^e ( t ) , t e [ t₀ , t ]

ется за решение задачи 2 .

стратегии условий

принима-

3. Численный эксперимент

Изложенная выше теория иллюстрируется на следующих числовых данных:

минимизирующее норму фазового вектора линейного динамического объекта в момент времени t .

Коррекция движения управляемой точки достигалась путем добавления управления u ⁰ ( • ) к базовому управлению на промежутке времени [ t ₀, t_{ ]

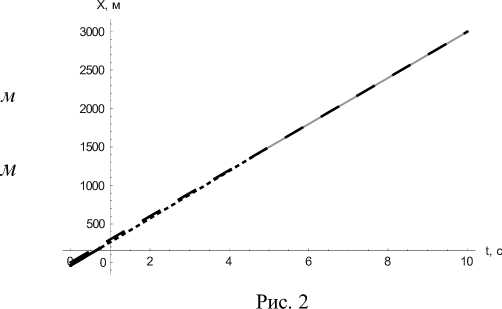
Ниже приведены графики (см. рис. 2–4) изменения геометрических координат управляемой точки, иллюстрирующие ее выход на базовую траекторию в момент времени t_x = 5 сек и дальнейшее ее движение вдоль этой траектории вплоть до достижения цели. Отклонение от цели составило μ 1 = 1.6994 м.

k = 0.45, m = 100 кг , g = 9.8 -м- , e = 30 м , сек ²

t ₀ = 0, T = 10 сек , ^ ( x , y ) =50 • sin ( 0.00005 • x • y )

x0 = -40 м, y0 = 20 м, z0 = 40 м, , xT = 3000м, yT = 100м, zT = ^(XT, yT ) = 32.51

, мм  м

^X 0    ³¹⁰     , y 0      ¹⁰     , z 0    ^-12.7⁵     ,

cек

cек tx = 5 сек .

cек

Тогда

Y, м

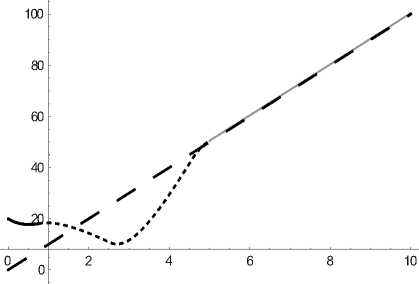
Рис. 3

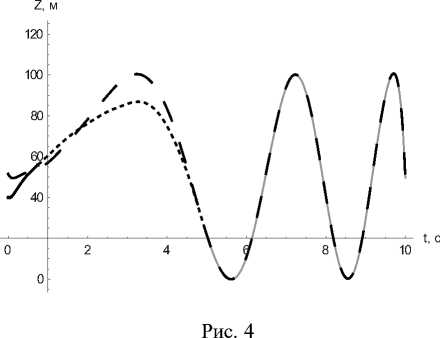
Откорректированное движение точки

Движение вдоль базовой траектории после отключения ДПУ в откорректированной системе

Базовый закон движе ния с базовым ПУ

Не откорре ктированное движе ние

При решении задачи 2 было найдено наименьшее время τ k = 4.3 сек. выхода фазового вектора   линейного   объекта в

£ ( t₀ , q ₀, т ) - окрестность начала координат. При этом имело место двойное неравенство.

0 < £0 (t0,q0,т) = 0.2009 < 0.3 = ^ Построено программное управление ue (t), t ^[t0,T], решающее задачу 2 для найденного момента времени τk = 4.3 сек.

Коррекция движения управляемой точки достигалась путем добавления управления u e ( • ) к базовому управлению на промежутке времени [ t ₀, т ]

Ниже приведены графики (см. рис. 5–7) изменения геометрических координат управ- ляемой точки, иллюстрирующие ее выход на базовую траекторию в момент времени τk = 4.3 сек и дальнейшее ее движение вдоль этой траектории вплоть до достижения цели.

Отклонение от цели составило μ 2 = 2.0214 м.

X, м

Y, м

Рис. 5

t, c

t, c 10

Рис. 6

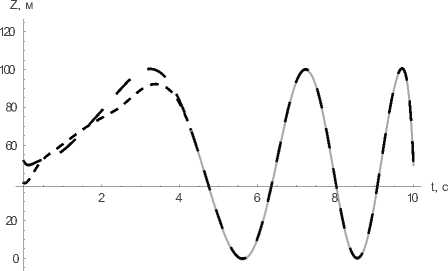
Рис. 7

Откорректированное движение точки

Движение вдоль базовой траектории после отключения ДПУ в откорректированной системе

Базовый закон движения с базовым ПУ

Заключение

В работе решена задача коррекции полета тяжелой материальной точки при наличии геометрических ограничений на дополнительные управления для случая, когда область достижимости линейного динамического объекта содержит начало координат.

Предложено два варианта решения задачи. В первом варианте дополнительное управление включается в тот момент времени, для которого начало координат выходит из области достижимости, оставаясь при этом в ее малой окрестности. Во втором решается задача быстродействия по выводу фазового вектора линейного объекта в малую окрестность начала координат.

Оба варианта решения задачи доведены до конкретных алгоритмов, и их эффективность проиллюстрирована на числовом примере.