Взаимосвязь сейсмических скейлингов на примере сейсмичности острова Кюсю (Япония)

Неравновесный характер сейсмического процесса, приводит к масштабной инвариантности физических полей, порождаемых сейсмогеиерирующей системой. Так, сейсмический процесс обладает скейлингом повторяемости землетрясений, описываемый законом Гутенберга-Рихтера. [1], который может быть выражен соотношением:

Е к N ^-ш                                    (1)

N — число землетрясений с сейсмической энергией Е, ш — константа, обычно интерпретируемая как "наклон графика, повторяемости". Кроме того, сейсмический процесс обладает локальными и глобальными скейлингами пространственных распределений эпицентров землетрясений и сейсмической энергии, что установлено с помощью мультифрактальпого анализа, данных сейсмических каталогов [2, 3, 4]). В работе [5] методом математического моделирования получены количественные соотношения, связывающие эти формы сейсмических скейлингов. Соотношения имеют вид:

• ¹    E-mail: stakhov@ifz.ru

а ® = ша® + const,                                     (2)

/ (а®) = / (as) ,                                             (3)

где a ® — индексы сингулярности мультифрактальиой меры, моделирующей пространственное распределение сейсмической энергии (сейсмоэнергетического поля), a^f — индексы сингулярности мультифрактальиой меры, моделирующей пространственное распределение сейсмических эпицентров (сейсмического поля), ш — абсолютное значение наклона графика повторяемости в энергетической форме (т.е. в форме (1)), / (а®) и / (a^f) — спектры сингулярностей соответствующих полей, const — эмпирическая константа, г — порядковый индекс боксов (ячеек) масштабной сетки. Индекс сингулярности определяется как:

а г = lim р г /т                                             (4)

г^0

где р_г — содержание меры в г-том боксе масштабной сетки, т — размер бокса (масштаб). Соотношения (2)-(3) были проверены с помощью структурного анализа, данных Южно-Калифорнийского сейсмологического каталога, (каталога. SCEDC — Southern California. Earthquake Data Center) [5], однако вопрос об их универсальности может быть решен только путем их проверки и подтверждения по данным сейсмических каталогов разных сейсмоактивных регионов.

Ниже приводятся результаты проверки соотношений (2)-(3) с использованием данных каталога. японской сейсмологической сети KiK-net. Проверка проведена, несколькими независимыми методами. Показано, что для сейсмического процесса, острова. Кюсю (Япония) соотношения (2)-(3) выполняются.

1.    Исходные данные

Основная масса, японских землетрясений происходит вдоль океанического желоба, расположенного восточнее сухопутных границ японских островов. Среди областей интенсивной внутриост-ровной сейсмичности выделяется остров Кюсю — наиболее южный из крупных японских островов. В данной работе структурный анализ сейсмичности острова. Кюсю проводился в рамках границ полигона размером « 100 х 100 км (координаты 33.29°-32.38° N, 130.52°-131.58° Е), сейсмический режим которого определяется в основном геодипамической активностью разлома. Футагава-Хинагу. За. инструментальный период сильнейшее из произошедших в этой области сейсмических событий — землетрясение Кумамото (16.04.2016, М = 6.5, Н =12 км).

В расчетах использовались данные каталога, сейсмологической сети KiK-net, одной из нескольких сейсмологических сетей, покрывающих территорию Японии. Сеть KiK-net объединяет сейсмостанции, оборудованные двумя широкополосными сейсмографами, один из которых установлен на. поверхности Земли, а. второй — в скважине на. глубине порядка. 100 м, что повышает точность определения параметров сейсмических событий и снижает влияние паразитных шумов. Сеть KiK-net ориентирована, на. запись и систематизацию информации о слабых событиях. Исследованная выборка данных каталога содержала порядка 1000-и событий в диапазоне магнитуд 2.5 <  М < 6.5 за. период 1996-2018 гг.

Для целей мультифрактальпого анализа, (подробное изложение теории см. [4]) территория полигона, покрывалась репормируемой масштабной сеткой квадратных боксов. Пространственные распределения эпицентров землетрясений и сейсмической энергии моделировались мерами p^f и р®, где верхиий индекс S соответствует сейсмическому полю, а Е — сейсмоэнергетическому полю. Содержание этих мер в г-тых боксах масштабной сетки оценивалось с помощью нормировки:

p f = ,V V . ,

р® = Ег/Ео, где N — число событий в г-том боксе, No — общее число событий в выборке, Ei — общая величина сейсмической энергии в г-том боксе, Ео — общая величина сейсмической энергии всех событий в выборке. Обработка, данных осуществлялась с помощью алгоритмов мультимасштабиого анализа, (box-counting и method of multipliers), реализованных для компиляторов Turbo С и Free Pascal.

2.    Результаты расчетов

Соотношение (2) показывает, что параметры локального скейлинга, сейсмического и сейсмо-энергетического полей в каждой точке связаны линейно, причем коэффициентом пропорциональности является ш - абсолютное значение наклона графика повторяемости в энергетической форме. Соотношение (3) показывает, что спектры сингулярностей (/(а)-спектры) сейсмического и сей-смоэиергетического полей связаны аффинными преобразованиями растяжения и сдвига, (т.е. с помощью преобразований растяжения и сдвига, один спектр может быть преобразован в другой). Следствием линейной зависимости (2) является равенство:

ш =

где г1 и г₂ — произвольные точки сейсмического и сейсмоэиергетического полей, имеющие одинаковые координаты. В частности, если максимальные и минимальные значения индексов сингулярности относятся к одним и тем же боксам масштабной сетки, то формула. (6) может быть записана, в виде:

, .   “ тах “min ш о        д ,

° “ тах “ min где “_тах и a_min — максимальные и минимальные значения индексов сингулярности соответствующих полей. Это условие автоматически выполняется в проверяемой модели [5], по в реальных выборках данных может нарушаться в силу ограниченного объема, данных в выборке (в силу нехватки данных).

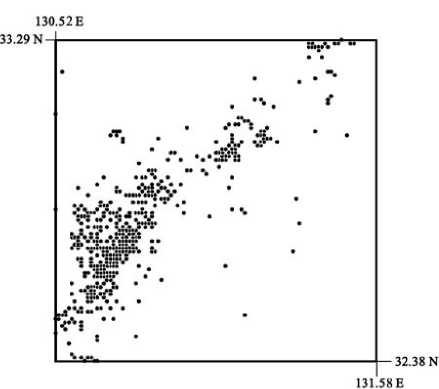
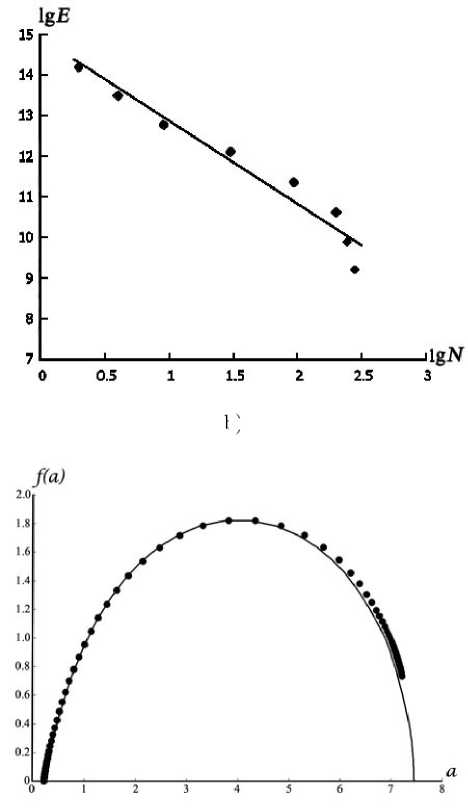
Перечисленные свойства, соотношений (2)-(3) допускают прямую экспериментальную проверку по сейсмическим данным. Так, на. рис. 1а. показано пространственное распределение эпицентров землетрясений в пределах исследовавшегося полигона. Рис. lb представляет традиционный график повторяемости землетрясений (в энергетической форме). Прямая линия на. рис. lb - график линейной регрессии, аппроксимирующий данные каталога, (точки). Абсолютное значение коэффициента регрессии можно рассматривать как оценку величины параметра ш, полученную с помощью построения графика повторяемости. В данном случае ш = 2.022 ....

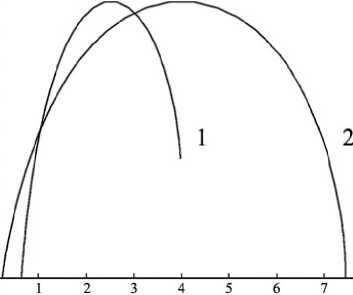
На рис. 1с представлены /(а)-спектры сейсмического и сейсмоэиергетического полей, построенных для исследовавшейся выборки. Максимальные и минимальные значения индексов сингулярности (т.е. точек, в которых ветви спектров достигают оси абсцисс) составили: а т _ах = 7.401..., “ m _in = 0.260..., а т _ах = 3.990..., a m _in = 0.550.... Подставляя эти значения в (7), получаем вторую оценку параметра ш: ш = 2.075 ..., причем в данном случае ш или "наклон графика повторяемости" (в энергетической форме) определен без построения самого графика, повторяемости, т.е. па. основе анализа, исключительно пространственных распределений сейсмичности. Как видим, в данном случае условие (7) выполняется.

На рис. Id показан /(а)-спектр сейсмоэиергетического поля (сплошная линия) и /(а)-спектр сейсмического поля (точки), преобразованный в соответствии с соотношениями (2)—(3), т.е. подвергнутый преобразованиям растяжения и сдвига. Параметр растяжения определен выше: ш = = 2.075.... Параметр сдвига const (2) может быть вычислен разными способами в зависимости от метода, минимизации невязок между спектрами. Учитывая сложную форму спектров, наилучшие результаты в данном случае дают не формальные методы подбора, параметра, сдвига, (метод наименьших квадратов, метод Колмогорова, или аналогичные методы), а. компьютерный перебор значений, минимизирующий невязки между вычисленными точками спектров (поскольку абсцис- сы этих точек не совпадают). На рис. Id показан /(й)-спектр сейсмического поля, преобразованный со значением const = -1.120 ....

а)

/(а)

2.0г

Ь

d)

Рис. 1. а) Пространственное распределение эпицентров землетрясений па исследовавшемся полигоне, Ь) График повторяемости в энергетической форме для исследовавшейся выборки данных, точки - данные каталога, прямая линия - график линейной регрессии, построенной по этим данным, с) Спектры сингулярностей сейсмического (1) и сейсмоэпергетического (2) полей, d) Результат наложения спектра сингулярностей сейсмического поля (точки) после преобразования растяжения и сдвига па спектр сингулярностей сейсмоэпергетического поля (сплошная линия).

с)

Рис. Id демонстрирует, что после преобразования растяжения и сдвига /(й)-спектр сейсмического поля практически совпадает с /(й)-спектром сейсмоэпергетического поля. Незначительное расхождение правых ветвей спектров объясняется нехваткой данных: форма правых ветвей /(й)-спектров определяется боксами масштабной сетки с наименьшим содержанием меры, что приводит к повышенным погрешностям и искажениям формы ветвей (в частности, нехватка, данных не позволяет довести правую ветвь /(й)-спектра сейсмического поля до оси абсцисс, т.е. приводит к разрыву скейлинга). Однако расхождение правых ветвей спектров в данном случае меньше погрешностей построения самих ветвей спектров.

Еще один способ проверки соотношений (2)-(3) заключается в построении непосредственной зависимости й ® от й ® в соответствии с выражением (2). Поскольку индексы сингулярности являются предельными характеристиками (4), а. на. сетках низкого разрешеппия оцепить пределы (4)

невозможно, значения щ аппроксимировались их приближенными оценками щ = lim p/ ~ P i /r. i—^0

График зависимости а ® от й® представлен на рис. 2. Необходимость использования приближенных значений й приводит к заметному разбросу точек на рис. 2, однако статистически множество точек сохраняет проверяемую зависимость. Линейная регрессия (график которой представлен па. рис. 2 прямой линией) имеет коэффициент регрессии, равный и = 2.091....

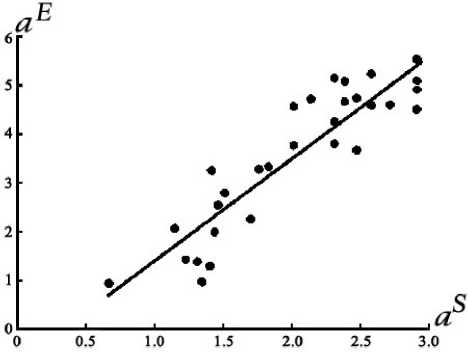
Рис. 2. График зависимости ар от а^ для всех непустых боксов масштабной сетки (кроме боксов, содержавших только по одному событию, т.е. непредставительных для статистического анализа). Прямая линия - график линейной регрессии, построенной по этим точкам.

Как видим, оценки параметра и, полученные тремя независимыми методами, различаются только в третьем знаке, а /(й)-спектры сейсмического и сейсмоэнергетического полей могут быть преобразованы один в другой с помощью аффинных операций растяжения и сдвига. Это позволяет утверждать, что впутриостровпая сейсмичность Японии на. исследованном полигоне подчиняется соотношениям (2)-(3) в пределах погрешностей имеющихся данных.

Заключение

Соотношения (2)-(3) показывают взаимосвязь всех известных на. сегодня форм сейсмического скейлинга, (кроме временного). Соотношение (2) связывает три формы сейсмического скейлинга: скейлинг повторяемости землетрясений и, локальный скейлинг пространственного распределения эпицентров землетрясений й ® и локальный скейлинг пространственного распределения сейсмической энергии й®. Соотношение (3) связывает глобальные скейлинги сейсмического и сейсмоэиергетического полей. Таким образом, соотношения (2)-(3) можно рассматривать как условия одновременного выполнения пространственных скейлингов и скейлинга, повторяемости сейсмических событий в едином сейсмическом процессе.

Взаимосвязь сейсмических скейлингов (2)-(3) существенно отличается от закона. Гутенберга-Рихтера. тем, что устанавливает соотношения между параметрами пространственных распределений эпицентров землетрясений и их сейсмической энергии (закон Гутенберга-Рихтера. (1) не содержит пространственных параметров сейсмичности). Возможность определения "наклона, графика, повторяемости" и без построения самого графика повторяемости (а только с помощью анализа прострапствеппых распределений сейсмичности) качественно расширяет физический смысл параметра и по сравнению с его значением в формуле (1): параметр и связывает сейсмическое и сейсмоэпергетическое поля в каждой точке, где значения полей отличны от пуля.

Результаты работы позволяют говорить, что взаимосвязь сейсмических скейлингов имеет характер закономерности, не зависящей от тектоники или географии сейсмоактивного региона. Соотношения (2)-(3) характеризуют неравновесную природу сейсмичности, а параметр и по сути является количественной мерой "степени иеравиовесиости"сейсмического процесса. По всей види- мости, соотношения (2)-(3) следует воспринимать как универсальный закон сейсмического процесса, который может быть назван обобщенным скейлипговым законом сейсмичности.