Задача базисности корневых функций дифференциального пучка 2n-го порядка с n-кратными характеристиками

DOI:

Постановка задачи

В теории краевых задач с параметром для обыкновенных линейных дифференциальных операторов, начиная с Лиувилля, Биркгофа – Тамаркина, четко выделены классы регулярных задач, собственные элементы которых обладают свойством базисности. К этим классам задач предъявляются естественные, но жесткие требования, в частности – различность корней основного характеристического уравнения [1]. В случае же кратности таких корней несоизмеримо возрастает трудность исследования. Случай единственного n-кратного корня рассмотрен в нашей работе [2].

В данной работе изучена задача для дифференциального оператора порядка 2 n с двумя n -кратными характеристическими корнями при распадающихся граничных условиях. Установлена эффективная формула разложения произвольной функции по корневым функциям задачи.

Рассматривается краевая задача для дифференциального выражения с параметром X

< 2^       ^ "

0 <  x <  1

^{1 (} У ) = jr ^{— X}2 У ^{( x} )

V dx      7

и краевыми условиями

U s ( У ) = d s y ^ = 0, s = 1,2n-1, U 2 n ( У ) = У ( 1 ) = 0. dx ^s

Введем в рассмотрение фундаментальную систему решений уравнения 1 ( у ) = 0:

/ \      i —1 X x           ( \ п — i —X x    •    1

y_z .⁽ x ⁾ = x e ,   У п ₊ i ⁽ x ⁾ = x e , i = 1, ⁿ .

Обозначим через Y ( x , X ) матрицу Вронского решений (3). Как следует из теоремы Лиувилля, ее определитель не зависит от x , то есть Y ( 5,X ) = Y ( X ) . Далее мы пользуемся функцией Коши:

	-У , ( 5 ) у ‘ ( 5 )	У 2 ( 5 )      .. у 2 ( 5 )      ..	У 2 п ( 5 ) у 2 п ( 5 )	— 1            ? | Y ( X ) npUx "  5                 (4) при x >  5
g ( x ЛА ><	у ! ’ п — ( ) У 1 ( x )	...           .. у 2 2 п — ' - )    .. У 2 ( x )     .. 0	.             ... У 22 п   ( ) -У 2 n ( x )

Функция Коши может быть определена не единственным образом. Функция

0 при x < 5 У1 (5)     ... У2п (5) У‘(5)     ...    у‘п(5) g(x,5,X ) = ^ ...            ...            ... УРп—”(?) ...   У22п   ( ) У! Сx)     ...    У2п Сx) , А, при x > 5                     (4.1) 1Y (X ) также служит функцией Коши.

Определяющим свойством этой функции служит то, что она:

• 1)    2 n – 2-кратно непрерывно дифференцируема по x и ξ на (0,1). При любом фиксированном x g ( x , 5 , X ) имеет непрерывные производные п -го порядка по 5 в каждом из интервалов [ 0, x ) , ( x ,1 ] Производная n – 1-го порядка при ξ = x имеет скачок, равный 1;

• 2)    при x # 5 Ц ( g ( x ,5,X )) = 0 .

Формула (4) удобна нам при Re X > 0 , а формула (4.1) - при Re X <  0 .

Дальнейшие суждения отнесем к случаю Re X > 0 , используя формулу (4) и опуская аналогичные суждения в случае Re X <  0 .

Лемма 1. Для любой 2 n – 1-кратно непрерывно дифференцируемой функции f ( x ), 0 <  x < 1, равной нулю со всеми производными при х = 0,1, справедливы формулы:

j g ( x ДХ ) f ^{( 2} n " ’^ ) d ^ = f ( x ) + O

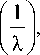
при |Х| >> 1 .

j g ( x ,u) f ^{( k} ) d ^ = j d k gdx^f £ ) d t x                           x ξ

при k <  2 n - 1.

Доказательство. К формулам (5), (6) приходим интегрированием по частям соответственно 2 n - 1 и k раз. Первый множитель в (4) получен из Y ( ^,Х ) заменой последней строки строкой У 1 ( x ) ,... у 2 n ( x ) . Вынося в этом множителе e"^ из первых n столбцов и e ~^ из последних n столбцов, придем к определителю, последняя строка которой имеет вид ( e ^{Х ( x} \... x n ^{- 1} e ^{X ( x} \ x n ^{- 1} e "^{X( x ч)},... e "^{X( x 1} ) ) , а предыдущие 2 n - 1 строк являются лишь многочленами от X степеней 0, 1, 2, . „ 2 n - 2. При этом коэффициенты многочленов зависят от ξ , что очевидно из формул (3). Для доказательства равенства (5), выполняя интегрирование по частям, находим:

j g (x ДХ)f(2 n-1)(^ )d§ = f (x) + j f (^) d2 ^g 2x    )d§.(6.1)

xx

Прежде всего отметим далее, что для определителя Вронского в знаменателе формулы (4) очевидна [принимая во внимание (3) и формулу Лиувилля] оценка:

|У(x,Х)® |Х|1+2+ .+2n1 C(e), C(e)> 0, при e>0, Vx e (e,1 - e).(6.2)

Покажем, что второе слагаемое в правой части равенства (6.1) имеет искомую оценку, d2n-1 g(xДХ)

указанную в (5). Для этого определитель в числителе дроби             представим в виде d ^2 n-

(2n)! его членов. При этом ограничимся членом d(Х, x), равным произведению элементов глав ной диагонали, так как оценки остальных членов вполне аналогичны:

2 n - 1           1       z/^{2 n-1} п (^}е^{Х(x -} ^ ⁾

d(Х,x)^ пХkqk(x)j f (^)d   pt,?n}1e----d^, k=0           x             d 4

I X|>> 1

интегрируя по частям, имеем

2 n - 1                1

d(Х,x)~ПХkqk(^)jf (^)Pk(^)eX(x-^)d^, pk(^),qk(^) - многочлены. Таким образом, приходим к к =0            x оценке:

d ( Х, x ) ~ Х^{1 + 2 +} ... + ^{2 n 2} при |Х| >> 1 ,

(6.3)

которая фактически справедлива для определителя в числителе формулы (4). Соединяя выраже- ния (6.2), (6.3), придем к оценке интеграла в правой части (6.1), имеющей вид O| 1 | и приводящей

V^Х J к формуле (5) при любом фиксированном x e ( 0,1 ) .

Приведем очевидное следствие леммы 1.

Утверждение 1. Пусть Cl - окружность с центром в начале X-плоскости и радиуса l, а f(x) – функция, указанная в лемме 1, тогда lim l ^да 0< x <1

t-t i■ i g (-'    )

d² n ^- ' f 6) d 2 2 n ^{- 1}

⁽⁵⁾ / \ ^d ^ = f ^{( x} ) .

Функция Грина и основная теорема

Последующее изложение свяжем с известным выражением мероморфной по X функцией Грина задачи (1)–(2), (см.: [1; 3, с. 46]):

G (x ЛХ ) =

А(x ЛХ) А(Х)

где ^{а( х )} = det { U s ⁽ у, ^{( x ))}} j

g ^{( x} ,5^,Х ) У 1 ^{( x} ) ... у 2 n ^{( x} )

	U 1 ( g ) x
А ( x ,^,Х ) =	...            U s ( y . )}/ n ,	(8)

U 2 n ( g i

В определителе А ( Х ) последние n столбцов и первые n столбцов получены друг из друга заменой X на - X . Последняя же строка в А ( Х ) равна (е^Х... е ^Х, е ^{- Х}... е ^{- Х} ) . Заметим также, что члены определителя А ( Х ) с индексами ( 1,2 ) ... ( 1,2 n - 1); ( 2,3 ) ... ( 2,2 n - 2 ) ;... ( n - 1, n ) , ( n - 1, n + 1 ) равны нулю. Указанные особенности позволяют сравнительно просто указать его члены с наибольшей степенью Х: n ( n - 1 ) . Таким образом

А ( Х ) = [ A ] Х ^{n ( n — 1 )} ( е ^Х - е ^{- Х} ) ,

где [ A ] = A + O |  | , A ^ 0 - константа. Мы получаем следующее утверждение.

v Х 1

Утверждение 2. Спектр задачи (1)–(2) исчерпывается асимптотическими при росте ν значениями X _v ® nv V- Т, v е Z .

Далее разложим числитель функции Грина на два слагаемых:

А ( x Л X ) = g ( x , ^, X ) А ( Х ) + Е ( x , ^, X )

где определитель Е ( x ,^,Х ) получен из (8) заменой нулем элемента в его левом верхнем углу. При этом первый столбец в Е ( x ,^,Х ) с учетом условий (2) и представления (4) имеет асимптотический по Х ^ да вид:

„ <      1        1        1 А ‘               .

е^ • 0,—_г-_г, _{9 9} ,...—,0 , ReX > 0 .

I , х 2 n - 1 , х 2 n - 2 , х , I ,

Принимая во внимание (11) и конструкцию Е ( x ,^, X ) , приходим (при Re X >  0 и x <  ^ ) к оценке

Л n ( n -1 )

^{Е (} x^-^{X :} X      е“’ ⁴’.

Согласно (9), (11) приходим к асимптотической по X ^ да при Re X >  0 оценке

E ( x ЛХ)     е ^^{( x -} ^ )

А ( Х )        X^{2 n - 1} , ^x <  ^ .

Принимая во внимание аналогичную (13) оценку при Re X <  0 , получим следующее утверждение.

Утверждение 3. Для любой непрерывной функции f(x), 0 < x < 1 справедливо равенство lim

I ^а>

1    г dX г E ( х ЛХ )

2пV—1 С , X 0 а ( х )

f ( S ) d S = 0 ,

где С , - окружность с центром в нуле Х -плоскости и радиусом п | I +-| .

^l                                                                                 I 2 )

В завершение нами устанавливается следующая теорема.

Теорема. Для любой 2 n – 1 раз дифференцируемой функции f ( x ), равной нулю вместе со всеми производными на концах 0, 1, справедлива формула разложения по корневым элементам задачи (1)–(2):

• 1    f dX\_H d.xd ^{2 — 1} f (^ )„

l -        Jr Г G ^{( X ЛА})         ^{d s} = ^{f ( X} ) .                     ⁽¹⁵⁾

0 < X < 1 ^{2ПЛ/ 1} C l ^X 0               ^d s

Доказательство. Согласно формуле (10) и утверждению 3 левая часть в (15) записывается в виде lim l ^to

•n¹ , ^ J g ⁽ X -^X ) ^C l      ⁰

d² n - 1 f ( S ) d S^{2 n - 1}

d S +

+ lim----;

^l ^” 2nV

__f dx f E ( X , 6 . Х ) d¹" ^{— 1} f ( e )

—

T C yJ   A ( x )    d 6 ² ■ ■   ⁶

Остается сослаться на утверждения 1 и 3.