Задача Коши для уравнения Лапласа с тремя независимыми переменными

Классическая теорема Коши-Ковалевской дает существование и единственность решения задачи Коши для дифференциального уравнения в частных производных с аналитическими коэффициентами. Однако существование решения гарантируется только в малом. Здесь будет изучаться задачи Коши для одного узкого класса уравнений, но решение будет получено в целом. Решение в целом получается за счет того, что уравнение рассматривается в комплексном пространстве.

Постановка задачи

Рассмотрим уравнение Лапласа d2f d2f d2f n

Af = / +    +    = 0, оx   оy    оz где х, у и z - независимые комплексные переменные. В (1) произведем следующую замену переменных:

f = x + iy, n = x - iy, f = z

Уравнение (1) примет вид

Л d ² f   d ² f _n

4—— + ^- = 0.

dfdn df2

Будем искать решение f уравнения (1), удовлетворяющее условиям

(1 * )

f f = 0 = ^{u ( f} n ),    If

= v ^{( f ,} n ), f= 0

где и и v - функции, голоморфные в некоторой области голоморфности B с C ² .

Функцию f можно представить в виде f = g + h , где g и h - решения уравнения (1), удовлетворяющие условиям.

°g g If=0 = u,     df

f = 0

I f = 0 = "-

d h d f

= v .

f = 0

Легко проверить, что функции g и h представляются следующим образом:

3 2 n, d и

w            £2 n g = У(-1)n 4n ^- ■

^{5 X}     2 n ! d f n d n

, n ’

(4а)

w                  ^2n + 1        л 2n h = y (-1)n 4n -^---d-^-

•

(4б)

n^ ⁷    (2 n + 1)! d f n d n n

Исследуем область сходимости этих рядов. Будем рассматривать ряд (4а). Ряд (4б) изучается аналогично.

Лемма. Если функция и голоморфна в бицилиндре D: {| ^f - f <  r , \п ^-%| <  r } , r >  ⁰ , то ряд (4а) для g сходится абсолютно и равномерно в круге K ₀: {| f | <  r , f = f ₀, n = П ₀ } .

Доказательство. Воспользовавшись оценкой получим

д ² n u d f n d n n

f=f o , П=П о

< M

( n !) 2

r ² n ,

w

I g | = X ( - 1) ' 4 "

й 2 n       л2 n„ f     du

n = 0

— (2 n )! d f n d n n

< M V 42 n £ ( ^f ) 2 ., n = X (2 n )!

Кибирев В.В. Задача Коши для уравнения Лапласа с тремя независимыми переменными

_                  4 n ( n !)² J 5_x2„                                      _х

Так как ряд V—-——(—) сходится при |$|<г, то ряд (4а) сходится - (2n)!   г абсолютно и равномерно в круге K0.

Заставим точку (50,П0) пробегать всю область голоморфности функций и и v. Рассмотрим бицилиндр D0i : {|5 - 50i |- r, П — П0J - Г}, r > 0, содержащийся целиком в области В, но такой, что всякий больший бицилиндр такого вида содержит точки, не принадлежащие области В. Согласно лемме, ряд сходится

W f=£ (-1) )- n=0           1

абсолютно

£ 2 n | л 2 п

5 I ди

(2 n )! [ d^ n дп

- и

5     д2nu I

--1---f

■ n 2 n + 1 d5 ⁿ dn n равномерно в

круге

K о i : {| 5 < г, 5 = ^ ₀₁, п = % i } . Образуем объединение K ( B ) = J K ₀ i ( 5ц Л0 1 ) ^е B всех кругов K ₀ i . K(B) содержит некоторую открытую в трехмерном комплексном пространстве С окрестность V(B) области В [2].

Если переменные х, у и z вещественны, то из леммы следует утверждение: если функции и и v вещественно-аналитические и разлагаются по функциям

Re [ ( x - x 0 ) + 1 ( у - у 0 ) ] ^Z [ ( x - x 0 )² + ( у - у 0 )² ]^h

(*)

Im [(x - x0)+ i(у - у0)]Z [(x - x0)2 + (у - у0)2 ]h в ряды, сходящиеся абсолютно и равномерно в круге (x - x0)2 + (у - у0)2 < r2, то ряды (4а) и (4б) сходятся абсолютно и равномерно на отрезке 10 :{|z| < r, x = x0, у = у0}.

Теорема 1. Если функции и и v разлагаются в ряды по функциям (*), сходящимся абсолютно и равномерно в круге K :{( x - x ₀)² + ( у - у ₀)² <  r ²} , то ряд

^

Z ² n Г -----Ia n u + (2и)! [

z

2 n + 1

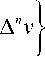
Z ( - 1)

n = 0

сходится абсолютно и равномерно в области

Q :{ z | <  r - 7 ( x - x 0 )² + ( у - у 0 )².

Для доказательства этой теоремы достаточно заметить, что для любой точки (x i , у) , лежащей в круге К, круг с центром в этой точке радиуса r - 7 ( x i - x ₀)² + ( у₁ - у ₀ )² лежит целиком в круге К.

Пусть М – поверхность, задаваемая аналитическим уравнением z=f(x, у). Пусть В – точка поверхности М, а U(B) – некоторая окрестность точки В и и – регулярная в U(В) гармоническая функция. В силу аналитичности функций и и £ = z - f ( x , y ) существует открытая окрестность V ( B ) с U ( B ) точки В, такая, что в V(B) имеет место представление [3]

W

^{u (} x , y , z ) = Е ^ Х ⁽ x , y )                           (7)

n = 0

для функции и, причем функции и п связаны рекуррентным соотношением n ( n - 1)(1 + f x2 + f y ) U n = ( n - 1) U n - 1 A f +

+ 2( n - 1)( f x "^ x + f y ^ )-A U n - ₂.

Из этого соотношения следует, что если u k = u k _{+ 1} = 0, то u_n = 0 при всех n >  к . Следовательно, два соседних коэффициента ряда (7) не могут одновременно обращаться в нуль тождественно без того, чтобы ряд (7) не обрывался. При k=0 это утверждение превращается в теорему единственности решения задачи Коши для уравнения Лапласа.

Теорема 2. Если ряд ( 7 ) представляет регулярную гармоническую функцию, то разность между показателями степени ξ в двух соседних членах не превосходит двух.

Утверждение этой теоремы остается верным и для более общих рядов ^

u = Е l ^ ( x , y , z ) ] n u_n ( x , y , z ), представляющих регулярные гармонические n = 0

функции. А в случае, когда поверхность М является плоскостью, т.е. рас- ^

сматриваются ряды вида u = Е z ⁿ u_n ( x , y ) , утверждение теоремы остается n = 0

справедливым и при наличии в уравнении младших членов специального вида.

Заключение

В статье доказываются 2 теоремы задачи Коши для уравнения Лапласа с тремя независимыми переменными в комплексной области.