Задача Коши в целом для бицилиндрической области голоморфности начальных данных
Автор: Кибирев Владимир Васильевич
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Функциональный анализ и дифференциальные уравнения
Статья в выпуске: 1, 2013 года.
Бесплатный доступ
В данной работе доказаны две теоремы о решении задачи Коши в целом для одного специального класса уравнений за счет того, что уравнение рассматривается в комплексной области.
Задача коши, голоморфные функции, бицилиндрическая область, аналитические коэффициенты
Короткий адрес: https://sciup.org/14835079
IDR: 14835079 | УДК: 517.946
Текст научной статьи Задача Коши в целом для бицилиндрической области голоморфности начальных данных
Классическая теорема Коши-Ковалевской дает существование и единственность решения задачи Коши для дифференциального уравнения о частных производных с аналитическими коэффициентами. Однако существование решения гарантируется только в малом. Здесь будет изучаться задача Коши для одного узкого класса уравнений, но решение будет получено в целом. Решение в целом получается за счет того, что уравнение рассматривается в комплексном пространстве.
Постановка задачи
Будем рассматривать задачу Коши в следующей постановке: найти решение уравнения d2и т , , x d2u n
( a )
— + ^ A^ ( x i ,..., xm )—— = 0 d z f! = i d X j d x^
(где Afl – аналитические функции, принимающие вещественные значения при вещественных значениях независимых переменных), удовлетворяющее условиям u\z=0 = f (x!,-, xm X |u |z=0 = g (x1,-, xm ) (в )
Возьмем в качестве области В , области голоморфности функций и и v , бицилиндрическую область D = D 1 ■ D 2, где D 1 - область в Z -плоскости с гладкой границей Г 1 ; D 2 - область в ^ -плоскости с гладкой границей Г 2 . Всякую функцию, голоморфную в D и непрерывную в замкнутой области D , можно представить следующим образом:
1г Г u(t,т)dtdT uZ п) = -т^ J ;. (1)
4 п Г , Г 2 ( t - Z )( т - п )
Поменяв порядок суммирования и интегрирования, получим g (Z, П, Z)
1 Г г u ( t, т ) у ( n !)24 n - Z 2
dtd T
4 п 2 J Г 2 ( t - Z )( т - п ) £ (2 n )! L ( t - Z ) T - П ).
аналогично будем иметь h (Z, П, Z)
1 Г r Z v ( t , T ) у ( n !)24 n - Z 2
4 n 2 J J( t - Z )( t - п ) n ^ 0 (2 n + 1)! L ( t - Z )( t - П ).
у Jn<_4 n =b (2 n + 1!)
Воспользовав-
(n !) ЛП n Рассмотрим ряды > ----4 v , n=0 (2n)!
шись формулой удвоения для гамма-функции, получим
V tT<" + 1)12 4nvn = ПУ [Г(n +1)1 4nv n=0 Г(2n +1!) t04n Г(n + 1)Г „ Г(-)[Г(n +1)12 = b ------i—vn = F (1,1;-; v), n=0 n !Г( n + -) 2 где F(а, в, Y, v) - гипергеометрическая функция Гаусса. И аналогично: ^ (n!) 4nvn = F(1,1;3;v). n=b(2 n +1)! V 2 7 Таким образом, решение задачи Коши в случае, когда начальные данные голоморфны в бицилиндрической области D и непрерывны в замкнутой области D , запишется следующим образом: f (6, п, Z) = — П Я 1 11 2 {—u^— F (1,1;1;'----) + (t — 6 )Т — п) 2 (t — 6 )Т — п) "v(t,Т) F (1,1;3; (t — 6 )Т — п) 2’ Z2 (t— 6 )(г—п) )} dtdT. Основные теоремы Теорема 1. Существует область голоморфности G(D) из пространства C3, такая, что каковы бы ни были начальные данные u и v, голоморфные в бицилиндрической области D и непрерывные в замкнутой об- ласти D , решение задачи Коши f голоморфно в области G(D). Если начальные данные аналитически продолжимы из D, то решение задачи Коши аналитически продолжимо из области G(D). Для каждой точки X границы области G(D) существует гармоническая функция, голоморфная в G(D), удовлетворяющая начальным данным, голоморфным в D, и имеющая особенность в точке X. Доказательство. Из представления (2) решения задачи Коши f6, п, Z) следует, чтоf6, п, Z) голоморфна там, где голоморфны функции Z2 f (U;1;— 2 (t — 6 )Т—п) з ■), F(1,1;3;— ' 2 (t — 6 )Т — п) Z2 ). Особенности этих функций располагаются на поверхности -2 = 1! (t— 6)(т —п) Рассмотрим множество Q = U РТ. Область G(D) является связной (t ,т)еГ1-Г2 компонентой дополнения CQ множества Q до всего пространства C3. Покажем, что G(D) - область голоморфности. Гипергеометрическая функция f(а, Р, y, v) голоморфна в плоскости с разрезом по лучу 1 < v <^, следова- тельно, функции Z2 f (1,1; 1;— 2 (t—6 )Т—п) з -), F(1,1;3;— ' ' 2 (t — 6)(т — п) Z2 ) голоморфны в пространстве С3 с выброшенной гиперповерхностью 1 < 62( t — 6)—1(т — п) <да. Обозначим эту область R. Область R будет областью голоморфности, так как плоскость с разрезом по лучу является областью голоморфности некоторой функции q(z) одного комплексного переменного z. Таким образом, G(D) - связная компонента пересечения областей голоморфности и содержит некоторое открытое связное множество, содержащееся в V(D). Значит, G(D) будет областью голоморфности. Граница области G(D) содержится в множестве Q, следовательно, для каждой точки X границы области G(D) найдется хотя бы одна поверх- ность PtT, содержащая эту точку. Функция 1 Г2 (t - 5 )-1(т - п )-1f (1,1;-; - 7------) 2 (t - ^)(т - п) является решением задачи Коши с начальными данными, голоморфными в D, а сама она голоморфна в G(D) и в точке X имеет особенность. Третье утверждение теоремы доказано. Второе утверждение доказывается очень просто. Область G(D) пересекается с пространством C2: {^ = 0} по области D, поэтому если начальные данные голоморфны в более широкой области B з D, то V(B) содержит точки, не принадлежащие V(D), а G(B) содержит точки, не принадлежащие G(D), и т.д. Далее будем рассматривать пересечение области G(D) с многообразием п = £ , lm z = 0 , на котором переменные х, у, и z вещественны. Для этого наложим ряд ограничений на область D. Области D1 и D2 будем считать симметричными относительно прямых £ = £ и п = П соответственно. Кроме того, будем предполагать, что при совмещении плоскостей ^ и п области D1 и D2 имеют непустое связное пересечение. Это значит, что пересечение бицилиндрической области D с многообразием ^ = п не пусто. В переменных х, y, z это означает, что в пересечении D0 = D11D2, лежащем в плоскости z=0, заданы условия задачи Коши, причем эти заданные функции аналитически продолжаются в 6ицилиндричсскую область D. Обозначим через H(D) такую область трехмерного вещественного пространства R3, которая содержит в качестве подмножества плоскую область D0 и является связной компонентой пересечения области G(D) с вещественным пространством R3: {lmx = lmy = lmz = 0}, вложенным в С3. Очевидно, что область H(D) содержится в прямом произведении области Do и оси Oz. Каждой точке границы области Do соответствует точка t границы области D1 либо точка т = t границы области P2, а функция f = (t - ^)-1 (соответственно f = (т - п)-1) голоморфна в D, удовлетворяет уравнению Лапласа и на прямой x + iy = t (соответственно x - iy = т) имеет особенность. Функция f в формуле (2) голоморфна всюду там, где голоморфны гипергеометрические функции, входящие в формулу (2), а особенности этих функций лежат на поверхностях z2 + (t - ^)(т - п) = 0. (3) Следовательно, в H(D) не должна попасть ни одна точка, лежащая на этих поверхностях. Пусть t = a + ib, т = а + ip, тогда пересечение соответствующей поверхности (3) с пространством R3 вещественных переменных x, y, z задается уравнением z2 + [x - a + i(y - b)][x - a - i(y - в)] = 0, которое эквива- лентно двум вещественным уравнениям (X - a+a)2 + (у - )2 + z = (a-a)2 + ( b-H)2, a-a b-β (b+р)(х —2—) -(a - a)(у —2™) =0" (4) Система (4) представляет окружность K, лежащую в плоскости, параллельной оси Oz и проходящую через точки (a, b, 0) и (а, в, 0). Для каждой точки t еГ, построим поверхность S(t), заполняемую окружностями (4), следующим образом. Рассмотрим область D2, симмет ричную области D2 относительно оси Ох. Каждую точку т* границы Г2 области D2 соединим отрезком прямой с точкой t. На этом отрезке, как на диаметре в плоскости, перпендикулярной плоскости хОу, построим ок ружность К(т*). Множество S(t) = UK(т*) будем называть сопутствующей поверхно- т *еГ * стью точки t. Так как Г является кусочно-гладкой кривой, S(t) с выброшенной точкой t - кусочно-гладкая поверхность. Поверхность S(t) замкнута и разбивает пространство R3 на две части. Ту часть пространства R3, в которой содержится множество D2, обозначим ^ (t) и будем называть ее присоединенной областью точки t. Аналогично строится сопутствующая поверхность и присоединенная область для любой точки т еГ2, только теперь вместо области D2 рассматривается область D*, симметричная области D1 относительно оси Ох. Очевидно, что та часть пересечения всех присоединенных областей, в которой содержится множество D0, и является областью H(D). Из структуры области H(D) вытекает простой способ ее построения в некоторых специальных случаях. Пусть области D1 и D2 совпадают и область D1 симметрична относительно оси Ох. Рассмотрим точку P е D1 и предположим, что D1 ограничивается простой замкнутой линией Г1, т.е. D1 односвязна. Через точку Р проведем хорду L(P) кривой Г1. На этой хорде, как на диаметре в плоскости, параллельной оси Оz, построим полуокружность в полупространстве z > 0. Эта полуокружность лежит на сопутствующих поверхностях концов хорды , а полукруг, ограничиваемый хордой и этой полуокружностью, принадлежит присоединенным областям концов хорды. Длина содержащегося в построенном выше полукруге отрезка прямой, параллельной оси Oz и проходящей через точку Р, равна произведению длин отрезков хорды кривой Г1, на которые она делится точкой P. Если рассмотреть всевозможные хорды кривой Г1, проходящие через точку Р, и построить на каждой из этих хорд, как на диаметре, полукруг, лежащий в плоскости, параллельной оси Oz, в полупространстве z > 0, то пересечение области H(D) с полупрямой Т(Р), параллельной оси Oz и выходящей из точки Р, лежащей в полупространстве z > 0, совпадет с пересечением всех построенных выше полукругов. Отсюда следует простой способ вычисления длины отрезка T(P)IH(D). Через точку Р проведем всевозможные хорды кривой Г1 и рассмотрим произведение длин отрезков хорды, на которые делит ее точка Р. Минимум этого произведения и есть длина отрезка T(P)IH(D). Таким образом, справедлива следующая Теорема 2. Пусть начальные данные задачи Коши для уравнения Лапласа голоморфны в бицилиндрической области D=D1⋅D1', где D1 – односвязная с кусочно-гладкой границей Г1, симметричная относительно оси lmξ = 0 область из плоскости переменного ξ, а D1'– та же область D1, лежащая в плоскости переменного η. Тогда граница области H(D) задается уравнением z2=Qm(P), P∈D, где функция Qm определяется следующим образом: плоскости ξ и η совмещаются с плоскостью хОу пространства R3, через каждую точку P∈D1проводятся всевозможные хорды кривой Г1, рассматриваются произведения длин отрезков хорды, на которые ее делит точка Р, а затем берется минимум этого произведения по всем хордам, проходящим через точку Р. Заключение Итак, в данной работе получено решение задачи Коши в целом для некоторого класса уравнений за счет того, что уравнение рассматривается в комплексной области. При выводе формулы (2) использовалось представление начальных данных задачи Коши интегральной формулой Коши. Если вместо интегральной формулы Коши воспользоваться формулой Бохнера-Мартинелли, то полученные результаты можно обобщить.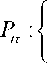
Список литературы Задача Коши в целом для бицилиндрической области голоморфности начальных данных
- Бицадзе A.B. Краевые задачи для эллиптических уравнений второго порядка. -М.: Наука, 1966. -204 с.
- Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. -М.: Гостехиздат, 1950. -436 с.
- Фукс Б.А. Специальные главы теории аналитических функций многих комплексных переменных. -М.: Наука, 1962. -420 с.
- Янушаускас А. К задаче Коши для уравнения Лапласа с тремя независимыми переменными//Сиб. матем. журнал. -1975. -Т. 16. № 6. -С. 1352-1363.
- Янушаускас А. К теории вырождающихся эллиптических уравнений//Сиб. матем. журнал. -1974. -Т. 15. № 6. -С. 1394-1405.


