Задача с нелокальными краевыми условиями на характеристиках для уравнения смешанного типа с двумя линиями вырождения

Задачи с нелокальными условиями возникают во многих областях физики, биологии, теории влагопереноса. Первые работы по нелокальным задачам появились у Л. И. Камынина, А. Ф. Чудновского, В. А. Стеклова. Позже появились работы А. В. Бицадзе, А. А. Самарского, А. М. Нахуше-ва, Е. И. Моисеева, Н. И. Ионкина и др. В 1969 г. А. М. Нахушевым были предложены нелокальные задачи нового типа, которые положили начало важному этапу в становлении и развитии теории краевых задач. Эти задачи были названы краевыми задачами со смещением, а за рубежом — задачами Нахушева. Они дают обобщение задачи Трикоми и включают в себя класс задач с самосопряженными операторами. В работах, посвященных исследованию задач со смещением для уравнений смешанного типа, краевые условия обычно содержат классические операторы. В нелокальных краевых задачах содержатся операторы более сложной структуры и операторы дробного интегро-дифференцирования.

Появились работы, посвященные численным методам решения нелокальных краевых задач.

К нелокальным задачам не применима разработанная А. А. Самарским общая теория устойчивости разностных схем, поскольку не имеет место положительность и самосопряжённость операторов, входящих в каноническую форму разностных схем, аппроксимирующих краевые задачи с нелокальными условиями. Численным, в основном разностным, методам исследования нелокальных задач посвящены работы А. В. Гулина, Н. И. Ионкина, В. А. Морозова, В. Л. Макарова, М. Х. Шханукова-Лафишева и др. [7; 12]. Разностным методам решения нелокальных краевых задач для уравнений теплопроводности посвящены работы [8–12].

Постановка задачи

Рассмотрим уравнение смешанного типа

I y k U xx + sgn ( xy )| x\ k u _yy = 0 , k = const >  0                (1)

в конечной односвязной области О , ограниченной кусочно-гладкой кривой Жордана о с концами в точках A ( 1,0 ) , B ( 0,1 ) , расположенной в первом квадранте x >  0, у >  0 и характеристиками AD : x^p + ( - у ) ^p = 1, CD : x + у = 0, BC : ( - x ) ^p + y^p = 1, 2 p = k + 2. Как уже указано, обозначено через О , , О₂ — гиперболические части смешанной области О , где x >  0 и x <  0 соответственно; О ₃ — эллиптическая часть области О ; з ( 3 ₂) — интервал 0 <  x <  1 (0 <  у <  1) прямой у = 0 ( x = 0). Под регулярным в области О решением уравнения будет пониматься функция u ( x , у ) из класса с ( o ) i с¹ ( о ) i с ² ( о , U о ₂ и о ₃ ) , удовлетворяющая уравнению и такая, что и_у ( x ,0 ) , u_x ( 0, у ) на концах интервала 0 <  x <  1 (0 <  у <  1) могут обращаться в бесконечность порядка ниже 1 - 2 Р , 3 — порядок дробных производных в нелокальном условии.

Задача А. Найти регулярное в области О решение u(x,у) уравнения (1), удовлетворяющее краевым условиям u (x, у ) = р(x, у), V(x, у )е о,(2)

u (x, у ) Odd = ci(x )

ai(у)DвyУ2в-1 u[Q(у)]+biу)DMу)2Р-1 u[Q(у)]=c2(у1 ^уе32,(4)

(3 = k /( 2 k + 4 ) , где Q₀ ( у ) , Q , ( у ) — аффиксы точек пересечения характеристик уравнения (1), выходящих из точки ( 0, у ) е3₂ с характеристиками OC,BC; ф ( x , у ) , а , ( у ) , b , ( у ) , с , ( x ) , с ₂ ( у ) — заданные непрерывные функции, причём       a 2 ( у ) + b 2 ( у ) ^ 0, у е 3₂ ;       ф ( x , у ) е С ¹ ( о ) ;

а , ⁽ у ) b , ⁽ у ), Ci ⁽ t ) е С ^{( 2} ’ h ) ⁽ 3j, h >  0 ; i = 1,2 ; D ^l _й y f , D^l y , f — операторы дробного в смысле Римана — Лиувилля интегро-дифференцирования [1].

Существование и единственность задачи А были доказаны [2] в случае, когда краевые условия (3),    (4) заменены условиями ai(t)D1-ви [Q0 (t)] + bi (t)DA Pu [Qi (t)] = ci (t )> V t е3 i, i = 1,2 .

Единственность решения задачи

Доказательство единственности решения задачи проведено в случае выполнения условий (2)-(4). Решение задачи Коши для уравнения (1) с данными на линии вырождения у = 0 в области О , даётся формулой [4; 5]:

b vp

^{3 - 4} Р

U ( x , у ) = — 2 p

К 2 Р> XV г ² ( Р ) ^x?

J t2 p—1(t2 p - a2)-1+Р (b2 -12 p)-1+PT(t) dt - a1 p b1p

- 243-1 p 112 - 23' Г2р—2 L2р — a2)-3 b2 — 12p )-3 u (t)dt, Г 2 (1 — в) аIp     V V где a = xp - (- y)p , b = xp + (- y)p . Также в области Q2:

b ₁ 1 p

u ( x , y ) = - 2^{3 - 4 3} p И xy f t ² p ^{- 1} ( t ² p - a 2 ) - ^{1 + 3} ( b 2 - t ² p ) ^{- 1 + в} _Ч ( t ) dt -Г 2 ( в )     aУ р

4 в - i Г(2-2 в)

^{2 p} Г ² ( 1 - в )

b ₁ 1 p

J t2p-2 (t2p - a2) 3 (b2 -12p) 3 u2 (t) dt, a1 p

где a 1 = y^p - ( - x ) ^p , b 1 = y^p + ( - x ) ^p , r ( a ) — гамма функция Эйлера.

Удовлетворим функцию u ( x , у ) краевому условию (3). Так как в точке ( x ,- x ) имеем a = 0, b = 2 x^p , то после замены переменной интегрирования по формуле £ = t ^{2 p} , переобозначив £ через t , затем 4 x^p через x , получим:

u Ь = 2 2- ^{4 в}- 1 ^p^ x ^p D -^ x -'* ³ ~ ( x ) -

• - 2 4 * - 2 'i' . ² 2 ' )' D^' x - ^{в -}"'⁽      ■x )                    ⁽⁷⁾

Здесь т 1 ( x ) = ~ 1 ( x ^{2 p} ) , u 1 ( x ) = ~ ( x ^{2 p} ) .

Отсюда с учётом (3) будем иметь:

- 3 в - ( 1 p ) Г ( 2 в )

Г(в)

x¹-^2в D^x ^{3 - 1}~ 1 ( x )

-

-

^{Г (} 2 ² в ' D 3 ^{- 1} x - ^{3 -( 12} р ) ~ ( x ) = 2^{2 - 4 3}c_y ( x ) . 0 x                   1                    1

1(1 - 3'

Вычислим теперь u [ Q o ( y ) ] , u [ Q i ( y ) ] , где Q o ( y ) = - ( y /2 ' ^{1 p} + i ( y /2 ' ^{1 p} , Q 1 ( y ) = - (( 1 - y )/ 2 ) ^{1 p} + i (( 1 + y )/ 2 ) ^{1 p} — аффиксы точек пересечения характеристик уравнения (1), выходящих из точки ( 0, y ) g3 ₂ с характеристиками OC , BC соответственно.

Так как в точке Q _o ( y ) имеем a 1 ^p = 0, b 1 ^p = y ^{1 p} , то после замены переменной интегрирования t = ^ 1 ^{2 p} и переобозначения ^ через t , а затем y² через y , будем иметь:

u [ Q o ( у ) ] = ^Г в y^{1-2 в} D^y* ^{3 - 1}~ 2 ( y )

-

24 ' ^{— 2}'^ — 2 в ^{D Ц1П} p ^)— ( y ) ■

—

где т 2 ⁽ У ⁾ = ~ 2 ⁽ У ² p ) , u 2 ⁽ У ) = u 2 ⁽ У ² p ) .

Аналогично вычислим u [Q1(y)]. Так как в точке Q1(y) имеем a1 p = y1 p, b1 p = 1, то, производя замену переменной интегрирования по формуле ^ = t2p , переобозначив £ через t, затем у2 через у, получим: u[бЯУЯ-^(1 — y)'—2в Dye(1 — у)1—~(у) —

• — 2 4 “ ^{— 2} Т ТТ^ D ?y ' У ■ p ( 1 — У ) ^— u ( у ) .        (10)

1(1—в)

Удовлетворяя (9), (10) краевому условию (4), будем иметь:

^ [ y ^{— 1} y ) + ( 1 — y в b ( y ) ] ~ ( y ) — 2 ^{в — 2} 5 (2^1 ^ y ) D ² ■ ^{— 1} D. -¹¹'² p ^)— у ( y )+ ^ У ) D ^ — y ) ² * ^{— 1} D^y -⁽¹² p > ( 1 — y ) ^— ■ ( y ) ] = c 2 ( У ) (11) После преобразования интегралов, входящих в полученное равенство, оно примет вид:

• ^^ ^[( 1 ^— y ^{) — e a} 1 < y ) + y ' bl^y )^{] c} ( y ) ^—

— 2 4 ^{в — 2 ^}F2Г _У 2 ^{в )}[ ⁽ 1 — y ) ^{1 — , a} 1 ⁽ y ^yD 2 -^{8 — 1} y ^{y CV2} p 5 ⁽ y ^{) +}

+ yb , y ) D y e ^{— 1} y -<¹² p > B 2 ( y ) ] = y ^e ( 1 — y ) ^e c 2 ( y ) .         (12)

Имеет место теорема единственности решения задачи.

Теорема. В области Q не может существовать более одного регулярного решения задачи А, если выполнены условия k < (75 — 1У2, (1 — y)1—в a1(y )+y1 eb1(y) ^ 0,

a1(y )* 0,

y ( 12 p ) + k

1+

V

Г      A 1— в

y

V1—y J

b1(y) a1 (у У

> 0, V y е 3 2 .

Доказательство. Пусть u(x,y) — решение однородной задачи А. Тогда в области эллиптичности уравнения (1) имеет место равенство [2]:

п 3

■ ^k ux 2 + xkuy ) dxdy = J x ^k T 1 ( x ) u 1 ( x ) dx + J y ^k T ₂ ( y ) u ₂ ( y ) dy . (13)

Полагая ci (t) = 0, i = 1,2, нетрудно установить справедливость сле- дующих неравенств:

J t ^k T i ( t ) u i ( t ) dt >  0, i = 1,2, t = x , y .

При c 1 ( x ) = 0 (8) примет вид:

Dx ' ~ (x) = kix20 ' D0;-x 0-(12pU (x), где ki =

Г(2 - 20) Г(0) 2в-3 Г(1 - 0) Г(20)

Подействуем на обе части последнего уравнения оператором D ° _x :

x ^{0 - 1} ~ 1 ( x ) = к 1 D 0 x x^{20 - 1} D x - ⁰ p U ( x ) .         (8 * )

После преобразования двойного интеграла (8 ) можно переписать:

~ 1 ( x ) = к D 0 ' ^-1 x ^{2 0} "б" p > ~ 1 ( x ) .

_т      Г( 1 -2 0 )г.-п, ^x x i ^{2 0} "^№ p и ( i ) di    „

Тогда —------ xu (x )t (x)dx = xu (x)dx ---;----1^—. Далее k 1    0                   0           0     (x - i )2 0

воспользуемся известной формулой для функции Г ( ц ) [6]

[ t ^{ц 1} cos ktdt = ^{Г ц )} cos — , k > 0,0 <  ц <  1.

^J ₀                  к ^ц 2

Полагая к = | x - i |, ц = 2 0 , получим:

1                          1 г

------= —т------- f t ^{2 0} 1 cos t x - i dt .         (15) I x - i ^{2 0} Г ( 2 0 ) cos np J                                '

С учётом (15) и формулы Г(z)г(1 - z) = п/sin nz, поменяв порядок ин- тегрирования, будем иметь: 1                                               1

п

2 k 1 sin п0

x

г

fv ^к ~fv^~fv^//v— fv fv^~*fv^//v f ~*fvVnQ/IV — л1 z/Л f/^{2 0A}Ht i x U 1 ( x ) т 1 ( x ) dx 1 / 1 ( x ) u 1 ( x ) dx I u 1 ( x )cos t x i I d i I t dt ,

где и " ( i ) = i ^{2 0} - ^{( 1}'²- y( i ) , Г 1 ( x ) = x ^{k - 2 0 2( 1,2} p ¹ .

Принимая во внимание равенства j u*(i)costi di

10                J

= 2~ * ( x ) cos tx J ~ * ( i ) cos t i d i ,

Гг x             f 1 J u(i )sin tidi L<0                 J j = 2~*(x)sintxJ ~*(i) sintidi , 0 после интегрирования по частям с учётом того, что у1 (x) = 1, получим:

X

П

2 k 1 sin пв

Г 1

J xk L? ( x ) ~ 1 ( x ) dx =

= f t ² ‘ ¹ dt j J )

। cos t S d S   +

—

V 0

x

/

Г1 *, .

| ~ (s )sin tsds

V 0

—

J /‘(x)dx Jt?!* (s)cos tsds

V 0

/

Г x

+ j~ 1* ( s ) sin t s d s

V 0

/

/

.

Очевидно, правая часть равенства будет положительной при выполнении условия у 1 ( x ) < 0, где / 1' ( x ) = ( k 2 в + ( 12 p )) x^{k — 2 в 1 + 1 1} 2 ^p ) . Или равносильное неравенство k <  (15 — 1 )/ 2 .

Положим теперь, что c ₂ ( y ) = 0 . Тогда уравнение (12) примет вид:

• -^~₂ ⁽ y ) = m 1 ⁽ y ) D ₀ ^{2 в — 1} y ”⁽¹² p ⁾ ~ 2 ⁽ y ^{)+ n} 1 ⁽ y ) Dy P ^{— 1} y -(^V2 p ⁾ ~ 2 ⁽ y ) , k ₂

^Zyy+ajCy^         (1 — у)1—вЬ(y)

д    ^{1 (} y ' ( 1 — y ) 1 ^{— в} а , ( y ) + y » b , С у ) ' 1 ⁽ y ) ( 1 — y ) ^{1 — в} а , (_ у ) + y¹ -^в Ь , ( y ) ’

k = 24в—2 Г(2 — 2 в )г(в)

• 2 =   Г(1 — в )г(2 в)

Из последнего уравнения запишем:

г ( 1 — 2 в ) k ₂

1 _k~                r _k~ ^y s ^{12 p} ~ ( s ) d s

J y ~2(y )~2(y )dy = J y ~2(y )m1(y )dy J —(

0                       0                     0

1       \        1 s ^{12 p} ~ ( s ) d s

+ J y ~2 (y ) n1 (y ) dy J (s — y)2 в.

С учётом формулы (15) и того, что Пsin2л:в = Г ( 2 в ) г ( 1 — 2 в ) , поменяв порядок интегрирования, будем иметь:

п

2 k ₂ sin пв

x 1

y

f y ^k ~ ( y ) ~ ( y ) dy = f t^{2 в 1} dt(m_x ( y ) ~ * ( y ) dy\ ~ * ( s ) cos t l y — ^ d s + 22             1_{2      2}

X              1                        1

+ Jt2в—1 dtJпх(y)~*(y)dyJ ~2*(s)cost|s — yds, 00    y где ~2*(y) = s ' 2p)~2(s), m1(y) = yk+(12p)m1(y), n1(y) = yk+(12p)n1(y).

После преобразований и интегрирования по частям с учётом того, что m1 (1) = 0, nx (0) = 0, получим:

, ^ _д J yk~ 2 ( У ) ~ 2 ( У ) dy = к 2 sin пр 0

«

f ^y

= -J t2 в-1 dt И m'( y) dy J ~(к }

к 0

A ²

। cos t ^ d ^ + У

f y

J ~ * ( ^ ) cos t ^ d ^ к 0

\2

-

У

J n ' ⁽ y ) dy

f 1                    A ² f 1                    A ²

J~2(£)cos td + J ~2(£)sintd к y                У к y               У

Правая часть равенства будет положительна при выполнении условий m' ( y ) < 0, n' ( y ) > 0. Вследствие введённых обозначений будем иметь:

m(y)+ n(y) = -^ , откуда «/( y ) = (12 p + к)y12 p+k1 - m'( y). Отсюда ввиду того, что (12 p + к)y ьк+12 p > 0 , то требование m^(у) < 0 автоматически повлечёт за собой условие й'( у )> 0. Запишем m/C у) в виде

m1'( у) =

y 12 p + к

f

1 +

к

( в в

:

b1( У)

0 -1⁽ у )_у

и требуем, чтобы

m 1 ' ( y ) < 0. Это

требование вполне будет обеспечиваться требованием теоремы y (1/2 p)+к

1+

к

Г Л 1- в у

к 1 - У У

b 1 ⁽ У )

01(У )У

> 0, V у е 3 ₂.

Отсюда заключаем справедливость неравенства (14). Из соотношений (13), (14) сразу следует единственность решения задачи А.

Существование решения задачи

Для простоты будем считать, что ^ ( x , у ) = 0 и кривая о совпадает с нормальным контуром о ₀: x ^{2 p} + y ^{2 p} = 1. Основные соотношения между ~ ( x ) , ~ 1 ( x ) , принесённые на Ц из эллиптической Q₃ [2] и гиперболической Q 1 частей смешанной области О соответственно, имеют вид:

~ ( x ) =- Я б^{в - 1}'^{2 2} p 1

_ ^ - x2 в

11 - ^ x |^{2 в}

~1 (^) d^ -

Т- 1 ?р - 12 [ ¹¹

2p J ^     [(^ + x)2в   (1 + ^x)2в

~ 1 ( ^ ) d ^ ,

Ф. М. Нахушева, В. А. Водахова, З. Х. Гучаева, А. Х. Кодзоков. Задача с нелокаль-

ными краевыми условиями на характеристиках ...

Исключая

2 4 - 8 ^{в 11p ) Г} Гв ) x . - = , D -, x , ^ x ) _

Г 2 'в D 0 - x " ^вp^ x ) = 2 4 "^ x )          (]7)

1(1 - 3)

~ 1 ( x ) из (16) и (17) и разделив обе части уравнения на

^Y 2 4 - 8 в - (1/ p ) ^Ф ^ ) x 1 - 2 в

2 Р         Г(в)

, получим:

DУ ^{- 1} j

О

_ F - x2 в

11 - F x ^{2 в}

~ (F) dF +

+ D- x ^{- 1} j

f-x-

F F F

~1F) dF +

⁺ B ] ⁽ x ) D о x ^- x" ^{р -( 12 p} u ⁽ x ) = g ] ⁽ x )

Здесь В       ^{2 Р} 24- 8 в - ( 1 p)_x - i +в ^{г( в )г(} 2 ^{2 р} )

Здесь B](x) = у 2 x    г(]-р)г(2в), g (x) = -2Р_ гв) x2в-] 2-2+4в+1 p)с (x) Y =    г2(в)

^{g 1}         у г ( 2 р )                   ¹ , ⁷ п 2^{2 - 4 в} г ( 2 р ) "

Подействуем на обе части (18) оператором D 1 - ^в . В результате, учитывая, что D a xD о xf = D a x ^{в f} , будем иметь:

D 0 -^{2 в} x ^{в - 1} j

_ f - x2 в

11 - F x\ ^{2 в}

t~1F) dF +

+ D 0 ;^{2 p} x ^{p - 1} j F^{3 - 12}

(F+x)57

(T+fF

~1F )dF -

+ DVB 1 ( x ) d 3;^X x ^{в -( 12 p} ) ~ 1 ( x ) = DVg ] ( x ) "          (19)

После ряда преобразований интегралов в уравнении интегральное уравнение (19) примет вид:

CU1(x)+ j k (x, t )l>i (t )dt = g (x),

где с = const, g(x) = c3x 1+1 (2p)-pdVx2в-1C](x), c3 =-2^1 г3!26в-3, k (x, t ) =

x1+12p 3 [k](x, t) + k2 (x, t) + kз (x, t)], x > t, x 1+V2p-р [k4 (x, t) - k5 (x, t) - k6 (x, t) + k7 (x, t)], x < t,

Нг Л = sin ^П Р - - - ( 1/2 p ) d_ Г     B^ ) d ^

1 (,) П dx J (x - 6 )1-в ({ -t f , к 2 (x, t ) =

1    d у - 1/2 Г       6^{в -} 1 d 6

Г(2в) dx     J(x - 6Г- (6 -1)2в , к3 (x) =

t^в - ¹² d г       6^{в - 1} d 6

Г(2 в) dx J (x - 6 )1-2в (t - 6 )2в , к4 (x ) =

t ^в - ¹² d f       6^{в - 1} d 6

Г(2в) dxJ (x - 6 )1-2в (t - 6 )2в , d f      6в-1 d6

5 ( ^, ) 1 ( 2 в ) dx J ( x - 6 ) ^{1 -} 2 ^в ( 1 - 6 ) 2 ^{в ,} z        t ^в - ¹² d J        6^{в - 1} d 6

6(x,t)=г(2в)dxJ (x-6)1-2в(1 +6)2- , к UtV - d (     6в-1 d6

7(        1-2/;) dx J (x-6)1-2в(t + 6)2- .

Далее рассмотрим о сновные соотношения между ~₂ ( у ) , ~₂ ( у ) , принесённые на 3₂ из эллиптической Q₃ [2] и гиперболической Q₂ частей смешанной области О соответственно:

^Т 2

( у ) =- ^ 6^{в - 12}

2 p ₀

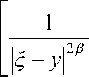
11 - 6 у |^{2 в}

~2 (6 ) d6 -

- Y_ ¹ ₆ - - 12 ² Р ^J 0

L(6 + у)2в (1 + 6у)2в J

-

~ 2 ( 6 ) d 6 ,

Гг<2|[(1 - у Г ва1(у)+ у1-вЬ1( у )]~2 (у )= 24в

2 Г((1^[(1 - ув"1^ )•

• D 0 - ^{- 1} у • ) ~ 2 ( у ) + у - ^в * , ( у ) D 2 - ^{- 1} у -1’2 p ' ~ 2 ( у ) ] + у - ^в ( 1 - у ) ^{1 - в} с 2 ( у ) . (22)

Исключая ~₂ ( у ) из (21) и (22) при a 1 ( у ) * 0, разделив обе части уравнения на 2^{4 в - 2} ^Г(^ -в^-^ ( 1 - у ) ^{1 - в} а 1 ( у ) , получим:

A ( у ) J 6 -^{- 12}

_ 6 - у2 в (1 - 6 у )2 в

—

~2 (6) d6 + A2 (у )J 6в-12

V6 + у )2 в

—

-

(1 + 6 у )2 в J

~ 2 ( 6 ) d 6 + D 0 ² у ^{- 1} у -^(V2 p ) ~ 2 ( у ) +

где A 1 ⁽ У ) =

+ A 2 ( У ) d ? ^{— 1} У -^{(12 p} ) ~ 2 ( У ) = f ( xX ), Y     Г ( 2 в ) Г ( 1 — в )   ( 1 — У ) ^{1 — в} а 1 ( У ) + У ^{1 — в} Ь 1 ( У )

2 p Г ( в ) Г ( 2 - 2 в ) 2 4 ^в

²         ( 1 — у ) ^{1 — в} а 1 ( у )

,

A 2 ⁽ У ) =

Г л ту;

к ^{1 У} )

b N, f . ⁽ У ) = ^— У' ^{в ( 1 —} У ^{) 1 — в} с 2 ⁽ У ) . ^а 1 ⁽ У )

Подействуем на обе части (23) оператором D

D 0^—2 "А ( У ) J 6 ^{в — 12}

+ D — ; ? a 1 ( у ) J е -"²

12 в

, 1 — 2 в 0 y

. В результате получим:

—

2 в

~ 2 ( ^ ) d ^ +

L fe + y ) ^{2 в} ( 1 + ^ y ) ^{2 в} J

—

~ 2 ( ^ ) d ^ +

+ У 2 p ) ~ 2 ( У ) + D 1 - y^{2 в} A 2 ( У ) D ¹ У 2 ^p ) ~ 2 ( У ) = D 0—^{2 в} f ( У ) (24)

После ряда преобразований уравнение (24) принимает вид:

A ⁽ У ) ~ 2 ⁽ У ) ⁺ J ^к ’ ⁽ У , t ) ~ 2 ^{( t} ) ^dt = f ⁽ У ) ,

где f ( у ) = — у ^{12 — в} ( 1 — у ) ^{1 — в} D 0 ^— у^2в у ^{1 — в} ( 1 — у ) ^{1 — в}

A ( у ) = ( 1 — у ) ^{1 — в} + cos 2 пв -^т ^{У )} У ^в + c ₄ ~ ^а 1 ⁽ У )

c 2 ⁽ У ) ,

^2 ^{) 1} - ^{e а} 1 ( ^{y )}± 2 ¹ Z ^e b 1 ^ ^{y )} a 1 ⁽ y )               ,

c₄ = — 2 2 ^— 4 ^в / ^Г(1 / ^в ) x [ 1 + n ctg 2 пв ] ,

⁴ 2 p      Г ( в ) Г ( 2 — 2 в )

у ^{12 — в ( 1 —} у ^{) 1 — в [ к} 4 ⁽ у , t ^{)+ к} 6 ⁽ у , t ^{)+ к 3 (} у , t ^)] , t ^ у ,

k Ч у , t M

y ^{V2 — в} ( 1 — у ) ^{1 — в}

к;(у , t )=в^ -У 1V ’ Г(2в) -У J к 3{У, t ) = t-А

2V ’ Г(2в) -У J к3(y, t ) = в12- d-V 3^ ’ Г(2в) dy J

, x t — 1 ^{( 2} p ) d t к ³ ( y , _t ) = t-^^—\ ⁴^’ ’ Г( 2 в ) dy J

^— k 1 ⁽ У , t ^)— k 2 ⁽ У , t ⁾⁺ k 3 ⁽ У , t ⁾⁺

_+ к 5 ( У , t ) + к 7 ( У , t )

A 1 ^ ) d :

( у — ^ ) ^в ( 1 — t ^ ) ^{2 в} ’ 4( £ d

( У — ^ ) ^в ( 1 + t ^ ) ^{2 в} A 1 ( ^ d

( у — ^ ) ^{1 — 2 в} ( t + ^ ) ^{2 в} A 2 ( ^ ) d ^

( У — ^ ) ^{1 — 2 в} ( t — ^ ) ^{2 в} ,

, t ^ У ,

k s( У , t ) =

t ^{1 ( 2} p ) d y       A ₂ ( 5 ) d ^

Г(2в) dy J (y - 5 )в (t - 5 )2в , k6(У, t ) =

t ^{в- 12} d г      A ( 5 d £

Г(2в) dy J (y - 5)в (t - 5)2в , k7(y, t ) =

t ^{в 12} d ^y      A₁ ( 5 d £

Г(2в) dy J (y - 5)в (t - 5)2в , k 8(y, t ) =

t ^{в 12} d ^y      A₁ ( 5 d £

Г(2в) dy J(y - 5)в (5 -1)2в

Таким образом, вопрос разрешимости задачи А эквивалентно редуцируется к вопросу разрешимости интегральных уравнений (20) и (25) относительно неизвестных функций ц( x ) , ~₂ ( y ) . Исследуем гладкость ядер k ( x , t ) , k *( y , t ) и правых частей g ( x ) , f ( y ) полученных уравнений. Из представления ядер k ( x , t ) , k *( y , t ) видно, что поведение их в смысле гладкости будет аналогично поведению ядер k ₃ ( x , t ) , k ₄ ( x , t ) и k * ( y , t ) ,

k * ( y , t ) соответственно.

Поэтому ограничимся исследованием свойств только этих ядер. Очевидно, гладкость ядра k ( x , t ) будет определяться гладкостью интегралов:

1 1 ( x , t ) = t ^в

-I

1 А)                _

dx J (x - 5) в (t - 5 )2 в

d ^

, 1 ₂ ( x , t ) = t ^в

1 dxx

dx J (x - 5 )1-2 в (t - ^ )2 в

d ^

После замены переменной интегрирования 5 = tz и применения формулы [6]

dzaF(a,в,Y,z) = aza--F(a +1,в,Y,z), |arg(--z)|<к dz и формулы автотрансформации

F(a, в, y, z) = (1 -z)Y-a-в F(y - a, Y - в, Y, z), |arg(1 - z) < n олуч 11 (x, t )=tв-1 (t/x)-2 в (1 - t/x)-1, 12 (x, t) = tв-1 (xh )2 в-1 (1 - xh)-1.

С учётом 1 ₁ ( x , t ) , 1 ₂ ( x , t ) ^k 3 ⁽ x , t ) =Г ( 1 в ) ⁽ xt ^{) 32} x - 1 ’ ^k 4 ⁽ x , t ) =

можно

( xt у-^{- 2}-

Г(2 в)       t

переписать ядра

—

—. Точно так же x

гладкость ядра k *( x , t ) будет определяться гладкостью интегралов:

1 3 ( У , t ) = t -1 ^{( 2} p )

1 4 ( У , t ) = t-1 ^{( 2} p )

d Г      A2 (^) di

dy J (y - S )1-2в (t - S )2в , d y     A2t-) d- dy J (y - ^ )1-2в (t - ^ )2в

После аналогичных вычислений имеем:

1 3 ( y ^, 1 ) = (- y/t ) ^{2 в} -^-Ъ ^, 1 41 y ^, t M yt ) ^{2 в - 1} ;  \

.

t y t                            t t y

С учётом последних рассуждений можем записать:

k *и а - A 2 ^{( t} ) и^у в + ¹ а - A 2 ^{( y}) (_v ; _ty в -i^_ ^{k 4 ( y -} t ) =Г ( 2 в ) 1 1 ^{( 2} p ^{) + 1 (} ) y - 1 ’ k ^{5 ( y} ’ t ) =Г ( 2 в ) 1 1 ^{( 2} p ⁾- ^{1 ( y}'t ) t - y "

Таким образом, ядра k ( x , t ) и k *( y , t ) непрерывно дифференцируемы в квадрате 5 1 х 5₂ при x ^ t , y ^ t и допускают оценки k ( x , t ) = o (1)| x - t | ¹, k *( y , t ) = o (1)| y - 1 | ', где o (1) означает ограниченную в 5₁ х5₂ величину.

Несложно также установить гладкость правой части в (20), (25). С учётом свойств дробных интегралов можно заключить, что g ( x ) g C ( 5 ₁ ) I C ¹ ( 5 ₁ ) , f ( y ) e C ( 5 ₂ ) I C ¹ ( 5 ₂ ) . Причём при x = 0, y = 0 могут обращаться в бесконечность порядка 1/2, а при x = 1, y = 1 они ограничены. Следовательно, при c ^ 0, A ( y ) ^ 0 система уравнений (20), (25) есть система сингулярных интегральных уравнений.

Условия c ² + п ² k ₁ ² ( x , x ) * 0, A ² ( y ) + n ² [ k ₁ * ( y , y ) ] ² ^ 0 , где k 1 ( x , t ) = k ( x , t )| x - 1 |, k * ( y , t ) = k * ( y , t )| y - 1 |, гарантируют существование регуляризаторов, приводящих сингулярные интегральные уравнения (20), (25) к уравнениям Фредгольма второго рода, безусловная разрешимость которых будет следовать из единственности решения задачи А.

По найденным ~(t) можно найти ~ (t), i = 1,2; t е31,52. Следова тельно, искомое решение задачи А в областях Q1, Q2 ищется как решение задачи Коши.

Заключение

В работе рассмотрено уравнение смешанного типа в конечной односвязной области О , ограниченной кусочно-гладкой кривой Жордана с т с концами в точках A ( 1,0 ) , B ( 0,1 ) , расположенной в первом квадранте x >  0, y >  0, и характеристиками AD , BC , CD уравнения. Существование и единственность решения уравнения c нелокальными условиями в случае производных дробного порядка 1 - в были доказаны в [2]. Отметим, что рассмотренная в работе задача относится к классу краевых задач со смещением, сформулированных А. М. Нахушевым [3].