Задача Трикоми для одного класса многомерных смешанно гиперболо-параболических уравнений

DOI:

Теория краевых задач для гиперболо-параболических уравнений на плоскости хорошо изучена [12], а их многомерные аналоги исследовано мало [8]. Задача Трикоми для указанных уравнений ранее исследована в [12]. Насколько известно, эта задача в пространстве не изучена.

В статье показано, что для одного класса многомерных смешанно гиперболопараболических уравнений задача Трикоми разрешима неоднозначно.

В работе [1] доказано, что для модельного уравнения однородная задача типа Трикоми (то есть измененное граничное условие) имеет нулевое решение.

1. Постановка задачи и результат

Пусть D — конечная область евклидова пространства Е _{т +1} точек (х 1 ,..., х _т , t), ограниченная в полупространстве t >  0 конусами К _о : | х | = t , К 1 : | х | = 1 — t , 0 <  t <  2 , а при t <  0 — цилиндрической поверхностью Г = { (x,t) : | х | = 1 } и плоскостью t = t ₀ = const , где | х | — длина вектора х = (х 1 , ...,х _т ) .

Обозначим через D + и D - части области D, лежащие соответственно в полупространствах t >  0 и t <  0 . Часть конусов К 0 ,К 1 , ограничивающих области D + , обозначим через S ₀ , S ¹ соответственно.

Пусть S = { (х, t) : t = 0, 0 <  | х | < 1 } , Г _о = { (х, t) : t = 0, | х | = 1 } .

В области D рассмотрим смешанно гиперболо-параболические уравнения

0=

т

Ажи — utt + Е Мх, t)uXi г=1

А _Ж М —

+ Ь(х, t)u _t + с(х, t)u,

U t ,   t <  0,

t >  0,

где А _ж — оператор Лапласа по переменным х 1 ,... ,х _т , т >  2 .

В дальнейшем нам удобно перейти от декартовых координат х 1 ,... ,х _т , t к сферическим г, 0 1 ,..., 0 _{m - 1} ,t , г >  0 , 0 < 0 1 < 2 п , 0 < 0 i < п , г = 2,3, ...,т — 1 , 0 = ( 0 1 ,..., 0 _{т -} 1 ) . Руководствуясь [12], в качестве многомерного аналога задачи Трикоми рассмотрим следующую задачу.

Задача T. Найти решение уравнения (1) в области D при t = 0 из класса С(D \ \ Го) П С 1(D) П С2(D+ U D-), удовлетворяющее краевым условиям иЪо = ф(г, 0),     и|г = ^(t, 0).

Пусть {Y^k _m ( 0 ) } — система линейно независимых сферических функций порядка п , 1 < к <  к _п , (т — 2)!п!к _п = (п + т — 3)!(2п + т — 2) , 0 = (0^..., 0 _{m - 1} ) , W 2, (S ) , I = 0,1,... — пространства Соболева, а S = { (г, 0 ) Е S, 0 < г <  1 .

Имеет место следующий результат [11].

Лемма. Пусть / (г, 0 ) Е W^S ) . Если I >т — 1 , то ряд

^ fc _n

/ (г, 0 ) = ЕЕ / ‘ №Е( 0 ),                     (3)

п =0 к =1

а также ряды, полученные из него дифференцированием порядка р <  I — т + 1 , сходятся абсолютно и равномерно, при этом

/ ‘ (г) = j / (г, 0 )Y;E( eW

Н где Н — единичная сфера в Em.

Через «мМ- ^а 1п ^(гА b ^k _n ^(г,t^), с £ (г,г) , р ^ р £ (r) , <⁽t) , ^т ^ ^(г), V;(г) обозна чим коэффициенты разложения ряда (3), соответственно функций a t (г, 0 ,t) p ( 0 ) , а_г^ р , г = 1,...,т , Ь(г, 0 ,t) p , с(г, 0 ,t) p , с(г, 0 ,t) p , р ( 0 ) , р (г, 0 ) , ^ (t, 0 ) , т (г, 0 ) = u(г, 0 , 0) , v (г, 0 ) = U t (г, 0 , 0).

Введем множество функций

В ¹ (S) = { /(г, 0 ):/ Е Wj(S),

^ fc _n

2 ^ Шп ^(г) 11 с 2 ₍₍₀ , 1 )) ⁺ 1^ ^(г) 11 с ([₀ , 1 _П)ехр²(п ^{2 + п(т — 2))}<  го ,

/ > т — 1 } .

Пусть а ₄ (г, 0 , t), Ь(г, 0 ,t), с(г, 0 , t) Е W ^l ₂ (D ⁺ ) С С (5 ⁺ ) , г = 1,..., т , I >  т + 1.

Тогда справедливо утверждение.

Теорема. Если р (г, 0 ) = г ³ р * (г, 0 ) , р * (г, 0 ) Е B ^j (S) , ^ (t, 0 ) Е W ^j (Г) , I >т + 1 , то задача Т разрешима неоднозначно.

Отметим, что неединственность решения задачи Т для модельного гиперболопараболического уравнения показана в [3].

Доказательство. В сферических координатах уравнение (1) в области D^ имеет вид

Lu = и _тт +

т —

г

- ur

1            т

---5u — U tt + ^2 а г (г, 0 , t)u_Xi + Ь(г, 0 , t)u _t + с(г, 0 , t)u = 0, t =i

где m - ¹       1      d           _n

5 = — ;> --------— —— I sin ^{m 3 1} 0 j ) ,

^=1 g3 slnm-3-1 0з d03               3 d0, , gi = 1, g, = (sin 01... sin 0,-1 )2, j > 1.

Известно ([11]), что спектр оператора 5 состоит из собственных чисел Л _п = п(п + + т — 2), п = 0,1,... , каждому из которых соответствует к _п ортонормированных собственных функций Y n _m ( 0 ).

При t ^

— 0 на S получим функциональное соотношение между т ( т, 0 ) и v (т, 0 )

вида

т _гг +

т

-

Т

Т

-

Т 2 St = v (т, 0 ).

Искомое решение задачи T в области D + будем искать в виде

∞

^к п

^м(т, м = 52 52 ^м п ^(т^^)у п^кт ^{( 0 )},

п =0 к =1

где м ^ (т,t) - функции, подлежащие определению.

Подставив (6) в (4), умножив затем полученное выражение на р ( 0 )

0 и

проинтегрировав по единичной сфере Н в Е _т , для м п получим ([2;4]):

р 0 ^м 0гг

-

p O ' O tt +

т

-

Т

^р 0 +

го к „

+ ЕЕ Pk,ML.

п =1 к =1

т   \

Е 4 г =0    /

^М 0 г

+ ^ 0 ^м 0 4 + ^с 0 ^м 0 +

-

Р П ^М П44

+

т

-

Т

^р П +

т   \

Е 4 г =1    /

й ^к пг

+ Ь^^Е

+ р

-

А п

. к

т

^ + Е ( 2 к„ - 1

-

г =1

^п^ ^мП}

= 0.

Теперь рассмотрим бесконечную систему дифференциальных уравнений

т

^Р 0 ^М 0 гг

_к — к Р ^км1гг

-

-

^p o ^M o tt +

Р ^{к м}ш +

т

т

-

Т

-

Т

^р 0 '^u 0 r

Р ^{к м} 1 г

-

= 0,

λ 1

Т 2 Р ^{к м к} =

-

\ ( т

^ 1524' О г

+ ^ 0 ^M 0 t

+ с , ^м 0

,

п = 1,

к = 1,к 1 ,

к — к Р П ^м Пгг

-

_к — к рп^

+

т

-

Т

-

кп-1   т г Е Е « кп к=1 I г=1

к

' гп - 1

^ML 1 r

р п ^ Лг

+ ^{к к} п

-

^А п к-к

Т 2 Р П ' П

1 ^U n - 1 t + (^С п - 1 +

+ Е(7

' к

' гп - 2

-

(п — 1)«

к

' гп - 1

г =1

Я^-Л,

к = 1,к „ ,

п = 2, 3,....

Суммируя уравнения (9) от 1 до к1, а уравнение (10) — от 1 до кп, а затем сложив

полученные выражения с (8), приходим к у равн ению (7).

Отсюда следует, что если {м п }, к = 1,к _п , п = 0,1,... — решение системы (8)-

(10), то оно является и решением уравнения (7).

Заметим, что каждое уравнение системы (8)–(10) можно представить в виде

^ML r ^— '^ t ^{+ (т}—1) 'L ^{— А} ? ^м п = кп^(Т,к,                ⁽¹¹⁾

т          т где /i(г, t) определяются из предыдущих уравнений этой системы, при этом /01 (г, t) = 0. Далее, учитывая ортогональность сферических функций У/т(0) ([1]), из (5) и из первого краевого условия (2) в силу (6) будем иметь

Тптг + —--1 Тпг - ^Тп = ^(г) 0 < г < 1,

Г и£(г,г) = фi(r), 0 < г < 2, к = 1Х п = 0,1,....

В (11)-(13), произведя замену и^г, t) = г(~-2~)и£(г, t) и полагая Е, = *+, п соответственно получим:

Lui = u^ + TT^^ui = /i (t, п),

( t + п ) ²

Tit +12 Ti = vi(t),0 < t < 2, ui(t, 0) = pi(t), 0 < t < 2,

^/ п ^{( t ,} п ) = ^{( t} + п )^^ + п , ^{t -} n ^), Ж) = (2 t )^ T i (2 t ), v i ( t ) = (2 t )^ v i (2 t ),

P ^ ( t ) = t ²   P i ( t ), A « = ((— - 1)(3 - —) - 4 A _n )/4, к = 1, к _п , п = 0,1,...

Используя общее решение уравнения (14) решение задачи Коши для уравнения (14) имеет

(см. [7]), в [2] можно показать, что вид:

^и^ п ) = 2 ^т i ⁽ п ⁾Д⁽ п ^, п ; ^{t ,} п ) +

+ "d ,f | v i ( b i )Л( Ь 1 , t i ; t , п )

V 2 п

-

₂T i ( t )E( t , t ,; t , п ) +

д

^T i ^{( t} i ) д^^R(t 1 ^, п 1 ; ^{t ,} п ^{) |} t 1 = п 1 Ж1 +

ξη

+ J J y i ( ^t i > п^Жь п х ; ^{t ,} пЖ 1Ж

I о

где E(ti,п1; t,п) = ^ц [(t1JJ(B-llГЖ^t^Г±tlli] — Функция Римана уравнения Lui = = 0 (см. [15]), а Рц.(^) — функция Лежандра, ^ = п + (т-3), д д^

t , - ! ,    (д№ д п 1 ⁺

д п 1 д д^ ¹ дЦ

)

^, t 1 = п 1

N± — нормаль к прямой t = п в точке (t1, п1), направленная в сторону полуплоскости

п < t .

Из (17) при п = 0, с учетом (16), получим интегральное уравнение Вольтерра первого рода дк(8) = У vJ(81)P; (|) d81, где д^) = V^(8) - — / ф,(81)P; (=1) d=i, 2 о

') = ф*<=), ^-о.

Уравнение (18) обратимо по формуле ([13]) (см. также [2])

v^k) = 1 у =1 (82 - =1)-2 р; (у) dg^ d 81.

Далее из (19), (20) имеем г, vkn(8) = f,(8) + У G,(8, 81)Ф,(8М1, где

V,(8) = -2/ 81(82 - 8?)-2p; (/)

-V 2 8 G „ ( 8 8 1 ) = 8 1 ( 8 2 - 8 ? ) ^{— 2} p ; (|) + / t( 8 ² - t ² ) ^{- 2} P ; ( ^{8: 1} ) p ; ( У ) dt+ + /8 1 ( 8 2 - t ² ) ^{- 2} P ‘ ( 8 ) P ‘ (У) dt.

Ограниченным решением уравнения (15) является функция ([9])

ξ

(82 - S1)t,(8) = I(8S281-S2 - 8S183-S1 )v,(81)d81 + c,(S2 - S1)8S1, 0 < 8 < 2,

(m—1)(

8 i = n + ^v 2 ' , 8 2 = - n - ^v 2 ' , c , — произвольная постоянная.

Подставляя (21) в (22), получим интегральное уравнение Вольтерра второго рода

ξ ф,(8) = F,(8) + У L,(8,81)^,(81)d81, где

ξ

F, ( 8 ) = (8 1 - 1)c , 8 ^{S 1 — 2} + ^— [[(8 2 - 1) 8 ^{S 2 —} 2 8 1 ^{— S 2} - (8 1 - 1) 8 ^{S 1 — 2} 8 3 ^{— S 1} ]У к ( 8 1 )d 8 1 , 8 2 - 8 1 J

ξ

(S 2 - S i ) L _n^ , ^ 1 ) = I [2 - 1)^^S2-2t^3-S2- 1 - 1)^^S1-2t^3-S1]Gn(t, ^)dt.

t 1

Определяя из (23) ^ П ( ^ ) , найдем

ξ тП(^) = ^1 ^kn(^i)d^i, 0 < ^ < 2, к = L"kTw n = 0,1,...            (24)

Таким образом, сначала решив задачу (8), (13) (n = 0) , а затем (9), (13) (n = 1) и так далее, найдем последовательно все и П (г, t) из (24), (15), (17), к = 1,к _п , n = 0,1,....

Итак, в области D+ показано, что j p(0)LudH = 0.                             (25)

н

Пусть /(г, 0 ,t) = Д(г) р ( 0 )Т(t) , причем Д(г) G V и V — множество, которое плотно в L 2 ((t, 1 - t)), р ( 0 ) G С ^ (Н ) - плотно в L 2 (H ) , а Т (t) G V 1 , V 1 — плотно в L 2 ((0, 2 )). Тогда /(г, 0 ,t) G V , где V = V ® Н ® V 1 . Как показано в [12], множество V - плотно в L 2 (D + ) .

Отсюда и из (25) следует, что j /(г, 0,t)LudD+

D +

=

1 - t

0 t

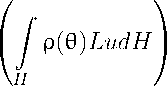
Д(г)Т (t)drdt = 0

и

Lu = 0, V (r, 0 ,t) G D ⁺ .

Учитывая оценки ([5; 11])

^W¹ <  ^c, H <  1, ^^(ch n ) | <  ^СexP⁽ P ^- 2) П , П > ⁰, ^{| k} n | <  ^C 2 ^{n m} - 2 , -Цр^ т к ⁰ ) <  C 2 ⁿ Т ^{+ p - 1} , | У о^: ,_т ^{( 0 ) |} = C i , C,C i = const,

3 = 1,m - 1, p = 0,1,..., а также ограничения на заданные функции, аналогично как в [2], можно показать суммируемость рядов в системах (8)–(10) и в уравнении (7).

Далее также можно доказать, что ряд

^ k _n

^{т (г}, ^{0 )} = ^гТ ^Т 1 ^(г)У о1 т ^{( 0 )} + ^ ^ ^п - ^{/ г Т} П ^(г)У Пкт ^{( 0 )           (27)}

n =1 k =1

сходится абсолютно и равномерно, если I >  ^{3 т} .

Таким образом, в силу (23), задача (4), (2), (27) в области D + имеет бесчисленное множество решений вида

^ k _n

^u(r, ⁰ , ^t) = ^г^^и 0 ^(г, ^t)y 01 m ^{( 0 )} + ^£ ^ги П ^(г, ^t)y n^km ^{( 0 )},          ⁽²⁸⁾

n =0 k =1

где функций u , (r, t) , к = 1, к _п , п = 0,1,... находятся по формуле (17), в которой v^E ) , т , ( ^ ) определяются из (24), (15) и принадлежит классу С (!) + ) П С 1 (D + U S' ) П С 2 (D + ).

Теперь задачу Т будем изучать в области D - .

В области D- рассмотрим первую краевую задачу для уравнения urr

+

m

-

r

- uT

--2 b u — u t = 0

с условиями

u|s = т(г, 0), u|r = ^(t, 0).

Решение задачи (29), (30) будем искать в виде (6). Подставляя (6) в (29), получим уравнение

Unrr - u,t + ^u, = 0, к = 1,кп, п = 0,1,..., при этом краевое условие (30) имеет вид un(r, 0) = 9,(r), Un(1,t) = <(t), к = 1, кп, п = 0, 1, ... ,

9 , ^(r) = {

T0(r),            ______ n-/T^(r), к = 1, кп, п = 1, 2,....

Произведя замену « , (r, t) = u , (r, t) — ^ , (t) , задачу (31), (32) приведем к следующей задаче

L«,k = vL — «kt + ^«k = J, (r, t),

«,(r, 0) = 9,(r), «,(1, t) = 0, 0 < r < 1,

J , (r, t) = ф , — I ? Ф , (<>- 9 ,k (r) = 9 ,k (r) — ф , (0).

Решение задачи (33), (34) ищем в виде « , (r, t) = « ^k„ + « 2 k, , где « ^k„ (r, t) — решение задачи

L«k, = Jnk (r,t),

«k„(r, 0) = 0,«k„(1,t)=0, а «kn(r, t) — решение задачи

L«kn = 0,

«2n(r, 0) = 9,(r), «kn(1, t) = 0, 0 < r < 1.

Решение вышеуказанных задач, аналогично [14], рассмотрим в виде

∞

«, (r,t) = ^Bs (r)Ts(t),(39)

S =1

при этом пусть

∞∞

J , (r) = £ a^„(t>Д . (r>, 9 П (r) = £ 6 k'₁„ Я , (r>.

S=1

Подставляя (39) в (35), (36) с учетом (40), получим

RSTT + ^Rs + U i = 0, 0

R«(1) = 0, |Rs(0)| < to,(42)

Tst + WT = -<„(t),

Ts(0) = 0.

Ограниченное решение задачи (41), (42) имеет вид ([9]):

Rs(t) = VT^v(Ys,nT), v = n + (m- 2), Jv(z^- функция Бесселя первого рода, Ys,n- ее нули, Ц = Y2n.

Решение задачи (43), (44) записывается в виде

t

Ts(t) = - У а^) exp[-Y2,n(t - УЖ

о

Подставляя (45) в (40), получим

∞

T2fn(T,t) = ^aks,n(t)Jv(Ys,nT), 0

S=1

∞

T-2дП(t) = ^bknjv(Ys,nT), 0

S=1

Ряды (47), (48) — разложения в ряды Фурье — Бесселя ([3]), если

^[Jv+1⁽Ys,n)]²J

^[Jv+1^(Ys,n⁾J²

о где Ysn, s = 1, 2,... — положительные нули функции Бесселя, расположенные в порядке возрастания их величины.

Из (45), (46) получим решение задачи (35), (36) в виде

^             t

^ln ^(T,t)

^-^ V^Tjv⁽Y_s,n^T){ / а^^)^exp^[-Y²„^{(t -} ^^)]d^^}, _S=1                о

где Qg_n(t) определяется из (49).

Далее, подставляя (39) в (37), (38), будем иметь

Tst + y2,„t = 0, решением которого является

^Ts (t) = exp(-Y2,_nt).                                  ⁽⁵²⁾

Из (45), (52), с учетом (40), получим

∞

• ^V2n^(r, ^{t) =} ^ V^n Jv⁽Ys,nT^ ^exp^(-Y^2,_nt),                   ⁽⁵³⁾

S=1

где b^„ находится из (50).

J,iL

Следовательно, решение задачи (29), (30) в области D^- есть функция

^ к_п

• и⁽г, 0, t) = ^ ^[<^(t) + vUr t) + ^(-г, ky    y^e),         ⁽⁵⁴⁾

n=0 k=1

где v^_n(r, t),V2_n(r,t) определяются из (51) и (53).

Учитывая ограничения на заданные функций ф(г, 0), ^(t, 0), а также оценки (26), аналогично [2; 14], можно показать, что полученные неоднозначные решения вида (28) и (54) принадлежит искомому классу.

Теорема доказана.