Задачи в системе деятельностного подхода как средство развития алгоритмического мышления

Обучение не возможно без деятельности, поэтому оно «должно быть нацелено не на передачу сообщений учебного характера, а на формирование мышления, способного эффективно усваивать необходимые знания» [6, с.306], созерцание деятельности учителя или сверстника не решит проблемы развития алгоритмического мышления.

В таблице 1 представлено соответствие принципов деятельностного подхода и условий развития алгоритмического мышления, формируемого в школьном курсе информатики.

Таблица 1. Принципы деятельностного подхода и условия развития алгоритмического мышления

Принцип деятельностного подхода	Условия развития алгоритмического мышления
Принцип деятельности . Знания даются не в явном виде, обучающийся сам добывает их через учебную деятельность.	Использование заданий на составление алгоритмов, по образцу и более сложной конструкции
Принцип целостности . Формирование целостного представления об окружающей действительности.	Усмотрение алгоритмической сущности, практико-ориентированные задачи на составление алгоритмов
Принцип минимакса . Обучающимся предоставляется возможность освоения содержания образования на максимальном для него уровне, и обеспечить при этом его усвоение на уровне социально безопасного минимума.	Применение  в  процессе  обучения дифференцированных заданий
Принцип психологической комфортности	Доброжелательная атмосфера, использование ментальных схем и неформальной записи алгоритмов
Принцип вариативности . Создание ситуации выбора, вариативность решения задач.	Рассмотрение нескольких алгоритмов решения одной задачи, понимание возможности поиска оптимального алгоритма.
Принцип творчества.    Предоставление возможности проявить творческое начало	Генерация нестандартных алгоритмов.
каждому обучающемуся

Вся учебная деятельность представляет собой процесс решения учебных задач, которые «выступают в качестве особого методического средства, способного обеспечивать усвоение учебного материла, интеллектуальное развитие обучаемых, удовлетворение их познавательных потребностей» [3, с.51]. Обучение на основе учебных задач переносит образовательные акценты с выслушивания обучающимися предметного материала на их учебную деятельность и развитие мышления.

По мнению В.В. Давыдова учебная задача «стимулирует мышление школьников к объяснению еще неизвестного, к усвоению новых понятий и способов действия» [2, с. 29]. А.Ф. Эсаулов подчеркивал, что «задачи должны не только и не столько способствовать закреплению знаний, тренировке в применении изучаемых законов, сколько формировать сам исследовательский стиль умственной деятельности» [11, с.7] и определял задачу как «более или менее определенные системы информационных процессов, несогласованное или даже противоречивое соотношение между которыми вызывает потребность в их преобразовании» [11, с.17].

Правильная постановка учебной задачи всегда нацелена на развитие обучающегося и представляет, сложную систему информации о каком-то объекте или явлении, часть сведений в которой известна (определена), а другая часть неизвестна (ее необходимо найти). Алгоритмическая задача -это задача, результатом решения которой является составленный алгоритм.

Процесс решения задачи предполагает определение неизвестной информации, поиск новых знаний, способов действий или согласование, соотнесение уже имеющихся знаний. В.В. Давыдов, рассматривая организацию процесса решения учебной задачи, представляет ее в виде составляющих:

• -    принятие от учителя или самостоятельная постановка учебной задачи;

• -    трансформация условия задачи для выявления взаимосвязей изучаемого объекта;

• -    моделирование взаимосвязей в предметной, графической и знаковой формах;

• -    выделение задач, решаемых общим способом;

• -    контроль за исполнением предыдущих действий;

• -    оценка освоения общего способа решения как результата решения данной учебной задачи [2].

В решении учебных задач результатом усвоения считается не только способность воспроизведения образцов, заданных учителем, но и процесс самостоятельного поиска решения. Учебный диалог, возникающий в процессе решения задач, представляет собой «специально управляемый обмен информацией между его участниками» [10, с.483].

Средствами решения задач могут выступать: знания, используемые обучающимся, формулы, схемы, тексты, различные инструменты. При изучении раздела «Алгоритмизация» главное, чтобы с помощью задач обучающийся не только освоил основные типы алгоритмов (ветвления, циклы с известным и неизвестным количеством повторений), научился использовать и обрабатывать данные различных типов, но также, чтобы процесс решения задачи способствовал развитию алгоритмического мышления.

Для этого можно рассматривать на занятиях доступные и понятные алгоритмы приготовления различных блюд, пользования бытовыми приборами и т.п. Генерируя такие алгоритмы, т. е., решая умственные задачи по составлению алгоритмов, обучающемуся не приходится обращаться к поиску какой-либо новой информации, он использует в качестве знаний свой жизненный опыт.

Содержательный анализ учебной задачи, соотнесение ее с группой уже решенных задач, приводит к выбору соответствующего способа решения, являются необходимым, но недостаточным условием развития алгоритмического мышления. Большое количество однотипных задач формируют установку на действие по готовому образцу, ограничивают поиск решения задачи (составление необходимого алгоритма) рамками уже известных, возникает «барьер прошлого опыта», или, по словам Талызиной Н.Ф., «автоматизация действия в одной из начальных форм препятствует переходу его в генетически более поздние формы» [9, с. 112]. Еще один аспект при разработке алгоритмов обучающиеся «должны уметь отслеживать, как новые исходные данные повлияли на конечный результат выполнения алгоритма» [5, с.93].

В школьном базовом курсе информатики система заданий по разделу «Алгоритмизация» условно может быть разделена на три группы в зависимости от формируемых умений [1, 4, 7].

Задачи первой группы не требуют построения математической модели, носят эмпирический характер, предполагают описание (или выстраивание) последовательности действий, выполнение которой приведет к требуемому результату.

К таким задачам можно отнести:

• -    составить алгоритм «определения времени показа по телевизору интересующего вас фильма», «перевод русского текста на итальянский» [7, с. 22-23].

• -    «Нарисуйте автомобиль своей мечты. Составьте словесный алгоритм работы» [4, с. 142]

• -    задачи на управление исполнителями

• -    «изобразите графически алгоритм приготовления яичницы» [4, с. 184],

Задачи второй группы требуют чаще всего построения одношаговой математической модели. Такие алгоритмы строятся по образцу уже известных конструкций, процесс решения можно отнести в большей степени к репродуктивной деятельности.

Примерами таких задач являются следующие задания:

• -    в учебнике для 9 класса - «составить алгоритмы вычисления площади треугольника» [7, с. 22] , в учебнике для 6-7 класса -«составить алгоритм вычисления площади прямоугольника» [4, с. 184],

• -    в учебнике для 8 класса - «составьте блок-схемы, которые описывают правила определения знака: а) произведения двух произвольных чисел; б) суммы произвольных чисел» [1, с. 131].

• 2.    Составьте алгоритм поиска для следующей задачи: на координатной плоскости заданы своими координатами N точек. Найти две самые удаленные друг от друга точки. Оцените временную сложность алгоритма. Рассмотрите два варианта алгоритма: с полным и с неполным перебором и сравните их.

• 3.    Составьте алгоритм для решения задачи, аналогичной предыдущей, с учетом того что точки расположены в трехмерном пространстве.

• 5 .6-1. Подсчитайте путь₊ который проходит Черепашка, когдн рисует следующие многоугольники си стороной 30 тагов: а) квадрат; б) треугольник; в) шестиугольник.

• 5 .ЙЯ. Подсчитайте путь, который проходит Черепашка, когда рисует:

Задачи третьей группы предполагают построение многошаговой математической модели и конструирование нового алгоритма. Они вызывают наибольшие затруднения у обучающихся из-за абстрактности, опоры на знания из других предметных областей.

Например, в учебнике И.Г. Семакина для 9 класса предлагается задание, представленное на рисунке 11, а в учебнике для 6-7 классов Н.В.Макаровой предлагается задание, представленное на рисунке 12.

Рисунок 11. Фрагмент учебника 9 класса [7, с.140].

• а) 18-угольник со стороной 10 тэгов; 6) 36-угйльннк со стороной Я тагов; ЗбО-угольняк по стороной 0,5 шага.

Рисунок 12. Фрагмент учебника 6-7 класса [4, с.197]

Основываясь на информационных моделях памяти и алгоритмического мышления. [6, 8], можно утверждать, что для решения задач первой группы обучающиеся опираются на чувственную область памяти, но в силу формулировки заданий не активизируют абстрактную область. Решение задач второй и третьей группы не опираются на чувственную область памяти. Для развития алгоритмического мышления при решении задач, желательна активизация всех областей памяти:

• -    Чувственной для хранения образов-отражений реальности полученных с помощью органов чувств (О );

• -    Модельной для хранения моделей- заменителей реальных объектов (О );

• -    Понятийной - хранение понятий, определений и свойств объектов (□);

• -    Абстрактной для хранения обобщенных образов ( △ ).

Проводя аналогию с «моделью памяти с точки зрения действий» [8, с. 13] можно построить модель развития алгоритмического мышления с учетом рассмотренных групп задач (см. рис.1).

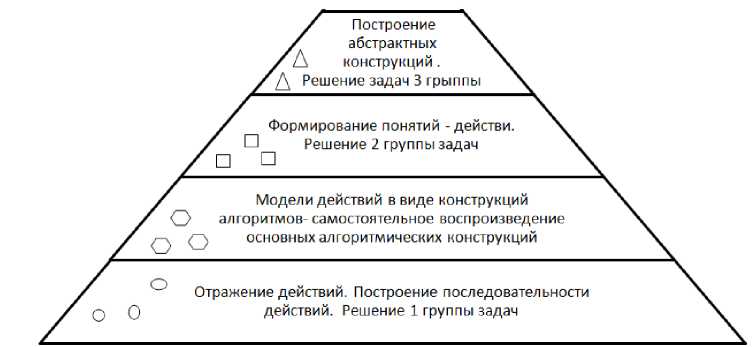
Рисунок 1. Информационная модель алгоритмического мышления.

При развитии алгоритмического мышления на основе решения задач, необходимо вовлечение в процесс мышления всех областей памяти, что облегчает процесс усвоения абстрактного учебного материала, за счет соотнесения его с ментально-эмпирическим опытом обучающихся.