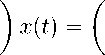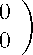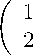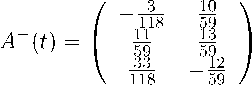Заметка о недоопределённых дифференциально-алгебраических уравнениях

Рассмотрим задачу

A(t)x 0 (t)+ B(t)x(t) = f (t),t G [0,1],                  (1)

где A(t), B(t) — (m x n)— матрицы, f (t) и x(t) — заданная n-мерная и искомая m -мерная вектор-функции.

О начальных данных будет сказано позже. Предполагается, что элементы A(t), B(t), f (t) обладают той гладкостью, которая необходима для проведения рассуждений.

При m = n и условии detA(t) = 0 будем иметь стандартные дифференциально-алгебраические уравнения (ДАУ). По качественному исследованию и численным методам решения начальной задачи ДАУ вышло и продолжает выходить огромное число публикаций, которые невозможно перечислить. Приведем лишь некоторые монографии, в которых приведены различные подходы к исследованию и разработке численных алгоритмов и прикладные задачи, описываемые ДАУ [2] , [6] , [7] , [8] , [12] , [13] . В этих же монографиях приведена обширная библиография по данному вопросу.

При m> n и условии rankA(t) < n, Vt G [0,1] мы имеем переопределенные ДАУ. Такие постановки задач возникают, например, при математическом моделировании некоторых технических процессов: модели гидроцепей [1] , уравнения со связями [6 , с. 524].

При m < n мы имеем недоопределенные ДАУ или ОДУ, которые даже при корректно заданных начальных условиях имеют бесконечное множество решений. Насколько известно авторам, для таких ДАУ практически нет исследований. Исключение составляет [13 , p. 511], где подчеркнуты принципиальные трудности исследования таких уравнений в терминах проекторов и приведено понятие их сложности (индекс один и два). Также отметим статьи [9] , [10] , где исследованы ДАУ с прямоугольными матрицами, для которых получены условия расщепления исходной задачи на более простые.

• 1    Постановка задачи

Вернемся к системе (1) при m < n. Вначале рассмотрим случай, когда rankA(t) = const = m Vt G [0,1],                  (2)

• т. е. матрица A(t) имеет полный ранг. Остановимся на выборе начальных условий. Если для стандартных ОДУ задают x o = x(0), то для (1) с условием (2) естественно задавать

A(0)x(0) = a,                            (3)

где a — заданный m -мерный вектор.

Приведем необходимые в дальнейшем изложении обозначения и сведения.

Определение 1. (см., напр., [2] , [4] ) Матрица D + называется псев-дообратной для матрицы D , если она является решением матричных уравнений:

• •    DD ⁺ D = D, D ⁺ DD ⁺ = D ⁺

• •    (DD+^D = D ⁺ D, (DD+y = D ⁺ .

Матрица D⁺ существует и определена единственным образом [2] , [3] , [4] . Если элементы матрицы D(t) G C [o 1] и rankD(t) = const, Vt G [0,1], то матрица D⁺(t) также определена единственным образом и ее элементы принадлежат C k 1] (см., напр., [7] ).

Рассмотрим систему линейных алгебраических уравнений (СЛАУ)

Gz = b,                              (4)

где G — (m х n) матрица; b — заданный; z — искомый вектор. Пусть z G Rⁿ множество векторов, которые минимизируют \\Gz — b\\ в евклидовой метрике. Вектор z * называется нормальным решением системы (4) , если z * G Z и при этом сам имеет минимальную норму в евклидовой метрике.

Нормальное решение (4) всегда существует и единственно [3] , [5] и находится по формуле (см., напр., [3] ):

z* = G+b.(5)

По аналогии с неопределенными СЛАУ приведем

Определение 2. Нормальным решением уравнения (1) с условиями

(2) , (3) назовем решением ОДУ вида:

X(t) + A+(t)B(t)x(t) = A+(t)f(t), t G [0,1],

x(0) = A+(0)a.

Рассмотрим другой случай, а именно rankA(t) = const = l < m,(8)

но rank[A(t) + (E — A(t)A+ (t)')B (t)] = const = m.(9)

Такие системы называют ДАУ индекса 1 [13]. Дифференцируя (1) и умножая полученное на матрицу V(t) = E — A(t)A+(t) в силу определения 1 (первое уравнение), имеем v (t)(A (t) + B(t))X (t) + v (t)B (t)x(t) = v (t)f 0 (t). (10) Суммой данной системы и исходной (1) является

A i (t)x ⁰ (t) + B i (t)x(t) = Mt), (11) где A i (t) = A(t) + V(t)(A 0 (t) + B(t)) B^t) = B(t) + V (t)B 0 (t), fat) = f (t) + V (t)f 0 (t).

При выполнении условий (8) и (9) можно показать, что rankA i (t) = const = m, то есть путем неособенных преобразований и дифференцирования мы свели ДАУ с условием (7) к задаче с условием (2) . Опишем выбор начальных условий для (11) , которые были заданы в виде (3) . Умножая (1) на матрицу V(t) = E — A(t)A ⁺ (t), имеем при t = 0 V (t)B(0)x(t) = V (0)f (0).

В отличие от случая (2) здесь rankA(t) = l < m, то есть СЛАУ A(0)x(0) = а имеет неполный ранг. Умножая (1) на матрицу V(t) и полагая, что t = 0, имеем V(0)B(0)x(0) = V(0~)f (0). Суммой данного начального условия и условия (3) является

(A(0) + V (0)B(0))x(0) = а + V (0)f (0). (12)

В силу (8) СЛАУ (12) имеет полный ранг, поэтому точно так же, как и в случае (2) ,

x(0) = (A(0) + V (0)B(0)) ⁺ (a + V (0)f (0)). (13)

Итак, мы редуцировали ДАУ (1) с входными матрицами, удовлетворяющими условиям (8) и (9) , и начальными условиями (3) к ДАУ (11) полного ранга с начальными условиями (13) , которое имеет единственное нормальное решение.

2 Численный алгоритм

Стандартные разностные схемы, разработанные для численного решения как ОДУ, так и некоторых классов ДАУ (при m = n), принципиально не применимы для рассматриваемых задач в силу того,что матрицы A(t),B(t) являются прямоугольными и могут иметь неполный ранг.

Ранее авторами были предложены коллокационно-вариационные схемы для задачи (1) [11] с начальными условиями x(0) = 0. Эти подходы не требуют вычисления производных выходных данных, весьма просты в программной реализации. Такие методы неплохо себя зарекомендовали на ряде известных тестовых примеров. Эти алгоритмы можно легко перенести на недопределенные ДАУ. Приведем один из таких методов с условием (3). Стандартно обозначим ti = ih, i = 0,1,...,N, h = 1/N, Ai = A(ti), Bi = B(ti) f = f (ti),xi ^ x(ti) и применим для (1) двухшаговую формулу дифференцирования назад [6]

A i+1 ^{(3 x} i+1    ^{4 x} i + x i - 1 ) + ^{2 hB} i+1 ^x i+1 — ^{2 hf} i+1 , i — 1, 3, •••> N .    ⁽¹⁴⁾

Предположим при этом, что матрица A(t) или A(t) + (E — A(t)A ⁺ (t))B(t) полного ранга. Начальные условия x g вычислены по формуле x(0) = A ⁺ (0)a для случая rankA(t) = m или по формуле (13) для случая rankA(t) = l < m и rankA(t) + V(t)B(t) = m. В результате, дифференцируя (14) на каждом интервале [t i _- 1 , t i=1 ], мы имеем недоопределенную СЛАУ размером m х 2n. Предлагается смотреть на (14) как на ограничения типа равенств для поиска минимума целевой функции, которая аппроксимирует квадрат нормы приближенного решения. Остановимся на выборе этой целевой функции. Пусть \\L i (t) | , t G [t i - 1 , t i+1 ] — интерполяционный вектор-полином второй степени, проходящий через точки (t i - 1 , x i - 1 ), (t i ,X i ), (t i₊1 ,x i₊1 ). Тогда \L i (t) \ ² , где t G [t _{i- 1} ,t _{i +1} ], будем находить по формуле:

\ L i (t) k ² = / t i+1 t i- i

[L > (t)L i (t) + (L > (t)) 0 L 0 (t) + (L > (t))"L i ° (t)] dt

~ ^{2 h} kx i+1 ^{— 2 x} i + x i - 1 1|² + ²h ||³ x i+1 ^— 4x i + x i - 1 1|² + ²h \ x i+1 \ ² .

Здесь норма вектора понимается как евклидова. В силу того, что умножение целевой функции на ненулевой скаляр не влияет на поиск аргумента условного минимума, мы будем иметь следующую задачу.

Найти h2

min \x i+1 — 2x i + x i - 1

II +y \ ^{3 x} i+1 ^{— 4 x} i + x i - 11| + ^{h k} x i+1 \

при ограничениях (14) . Так как шаг сетки мал, отбросим последнее слагаемое в (15) . Тогда на каждом интервале [t i - 1 , t i+1 ] получим задачу на условный минимум: найти minФ(x i+1 , x x i ), где

Ф(x i+1 , X x i ) = \ x i+1 — 2x i + x i - 111² + h- \ 3x i+1 — 4x i + x i - 111² ,   (16)

при ограничениях (14) . Стандартным образом, используя метод множителей Лагранжа, перейдем от данной задачи к задаче на безусловный минимум функции Лагранжа:

Z^{( x} i+1 , x i , ^Л) = -4- ||^—x i+1 + ^{4 x} i ^{— 3 x} i - 1 \ ² + ||^x i+1 ^{— 2 x} i + ^x i - 1 1|2 +

+Л> [(3Ai+1 + 2hBi+1)xi+1 — 4Ai+1xi + Ai+1xi-1 — 2hfi+1] , где Л = (A1,A2,...,An)T - m-мерный вектор множителей Лагранжа. Векторные аргументы xi+1,xi, Л, при которых функция (17) будет достигать минимума, удовлетворяют следующей СЛАУ

/ (2 + h^ )E        — (4 + 2h ² )E (3A i+1 + 2hB i+1 ) > \ / x i+1 \

I —(4 + 2h2)E     (8 + 8h2)E    —4A>1             I I XiI

\ 3Ai+1 + 2hBi+1 —4Ai+1       0                  /

/ —(2 + 2h^E \       / 0

= 1 (4 + 6h2)E    I xi-1 + I 0

\ — A i+1       /          \ 2f i+1 /

Начальное условие в зависимости от матриц A(t), B(t) нужно находить либо по формуле x g = A ⁺ (0)a, либо по формуле (13) .

3 Численные расчеты

Приведем численные расчеты модельных примеров. Здесь принято обозначение err = max ||xi — x(ti)k, а норма n-мерного вектора у за-i=i,N дается как ||у|| = max \yj|, где Xi находим по алгоритму (18), x(ti) — 1

Пример 1.1 Рассмотрим недоопределенное ОДУ

(1 2)x⁰(t) + (3 4)x(t) = 0, (1 2)x(0) = 5.

Псевдообратная матрица: A⁺(t) = (1/5 2/5)^T.

Нормальное решение данного примера является решением системы ОДУ

x⁰(t) +

3/5

6/5

4/5

8/5

x(0) =

Данная задача имеет следующее решение: x(t) =(exp( — уt), 2exp( — 11 t))^T. Результаты расчетов этого примера представлены в таблице 1.

Таблица 1

h	0.1	0.05	0.025	0.025
err	0.2	0.1	0.0543	0.0276

Пример 2. Рассмотрим недоопределенное ДАУ

/ 1 2 3 A 0, . / 1

_{0 0 0}x (t)+   ₂

11      6    123       6

_{3 0}   x(t) =   ₀   ,    _{0 0 0}   x(0) =   ₀   .

Продифференцируем вторую строку

з А 0/л ( 1 1

₀x (t)+   _{0 0}

1       6    123       6

₀   x(t) =    ₀   ,    _{2 3 0}   x(0) =    ₀   .

Псевдообратная матрица:

Нормальное решение данного примера является решением системы

ОДУ

-118  -118

533     533     533

118     118118

x(0) =

-9/59 6/59 117/59

Данная задача имеет следующее решение:

x^(t) =⁽-exp^(-19 t), exp^(-19t), 117 exp^(-19 t^))T. 59      59   59      59   59       59

Результаты расчетов этого примера представлены в таблице 2.

Таблица 2

h	0.1	0.05	0.025	0.025
err	0.024	0.01	0.0043	0.002

Расчеты показывают, что алгоритм справляется с решением недоопределенных ОДУ и ДАУ с первым порядком точности.

Заключение

В статье было введено понятие нормального решения для неопределенных ОДУ и выделенного класса ДАУ. Был предложен достаточно простой алгоритм для приближенного нахождения их нормального решения. Данный алгоритм был протестирован на модельных примерах, которые продемонстрировали его работоспособность. В дальнейшем авторы планируют создать другие, более точные, методы.