Зависимость электрического сопротивления углеродной нанотрубки с металлическим типом проводимости от механического нагружения и интеркалирования серой

Элект^онные и механические свойства угле^одных нанот^убок (УНТ) являются п^едметом интенсивных исследований в связи с пе^спективой их использования в мик^оэлект^онике, сен-со^ике, мик^оэлект^омеханических системах (МЕМС) и т.п. В связи с п^иложениями все больший инте^ес п^ивлекают воп^осы, касающиеся влияния на эти и д^угие свойства УНТ их взаимодействия с ок^ужением. Поскольку т^убки полые, то ино^одные атомы могут ^асполагаться как сна^ужи, так и внут^и них (инте^каляция). С последней возможностью связаны надежды на уп^авление свойствами т^убок.

По с^авнению с индивидуальными нанот^убками механические и элект^онные свойства ин-те^кали^ованных нанот^убок изучены го^аздо хуже, несмот^я на то, возможность инте^каляции экспе^иментально была обна^ужена вско^е после отк^ытия самих нанот^убок [1]. В частности, УНТ, заполненные халькогенами, стали изучаться еще в начале 90-х годов п^ошлого века в связи с капилля^ными явлениями [2]. Однако, несмот^я на п^ог^есс в синтезе инте^кали^ованных УНТ, до настоящего в^емени отсутствует целостное понимание влияния заполнения на их ст^ук-ту^ные и элект^ические свойства, не гово^я уже о зависимости этих свойств от механического состояния (дефо^мации) т^убок, п^о кото^ую по нашим данным неизвестно пока ничего. В то же в^емя связь между элект^ическими свойствами УНТ и их механическим состоянием п^едставля-ет большой инте^ес в связи с нуждами наносенсо^ики.

В связи со сказанным выше п^едставляет инте^ес тео^етическая оценка элект^ических свойств дефо^ми^ованных УНТ как «пустых», так и заполненных. В данной ^аботе с помощью неэмпи^ического квантовомеханического модели^ования изучается зависимость элект^ического соп^отивления однослойной угле^одной нанот^убки с металлическим типом п^оводимости от ее дефо^мации-^астяжения вдоль оси и сжатия в нап^авлении, пе^пендикуля^ном оси нанот^убки. Рассмат^ивается также влияние на эту зависимость инте^каляции УНТ се^ой.

Модель

П^и изучении влияния ^астяжения на элект^ическую п^оводимость УНТ в качестве объекта модели^ования выби^ался ф^агмент УНТ (7,7) длиной 1 нм (112 атомов угле^ода). П^и модели-^овании п^оцесса сжатия УНТ в нап^авлении, пе^пендикуля^ном оси, необходимо ^ассмат^и-вать нанот^убки большей длины, поэтому здесь ^ассмат^ивался ф^агмент УНТ (5,5) длиной 1,7 нм (140 атомов угле^ода).

Модели^ование п^оводилось с использованием метода не^авновесных функций Г^ина, ^еа-лизованного в квантово-механическом пакете TranSiesta [3], бази^ующемся на фо^мализме псевдопотенциала для уменьшения вычислительной сложности задачи. На сегодняшний день этот п^ог^аммный пакет наиболее за^екомендовал себя п^и изучении элект^ической п^оводимости молекуля^ных комплексов и нанот^убок в том числе. В вычислениях использовались обменно-ко^^еляционный функционал Капе^лея–Алде^а (Ceperley and Alder) (п^иближение локальной плотности – LDA) и базисный набо^ дубль-зета (DZ). В ^аботе п^именялись псевдопотенциалы, полученные с использованием упомянутого функционала Капе^лея–Алде^а по методике Н. Т^оуллие^а и Ж.Л. Ма^тинса [4]. Валентные конфигу^ации для атомов угле^ода и се^ы выби-^ались как 2s22p23d04f 0 и 3s23p43d04f 0 соответственно.

В упомянутом методе ^ассмат^иваемый ф^агмент сочленяется с двумя полубесконечными элект^одами (^ис. 1). Для исключения контактных явлений в качестве элект^одов использовались УНТ с теми же индексами хи^альности, что и у исследуемого ф^агмента. П^и модели^ова-нии сжатия УНТ в нап^авлении, пе^пендикуля^ном ее оси, этот ф^агмент ^азбивался на 3 области (^ис. 2): с замо^оженными степенями свободы атомов угле^ода (обеспечивает контакт с элек-т^одами), область «свободных» атомов угле^ода и дефо^ми^уемую область. Вто^ая область вводится для связи фикси^ованных концевых областей с цент^альной областью, где фикси^ованны-ми являются y -компоненты сдвинутых в п^оцессе дефо^мации атомов ( z нап^авление оси нано-т^убки).

Атомы с замороженными степенями свободы

Деформируемый фрагмент

Правый электрод

Левый электрод

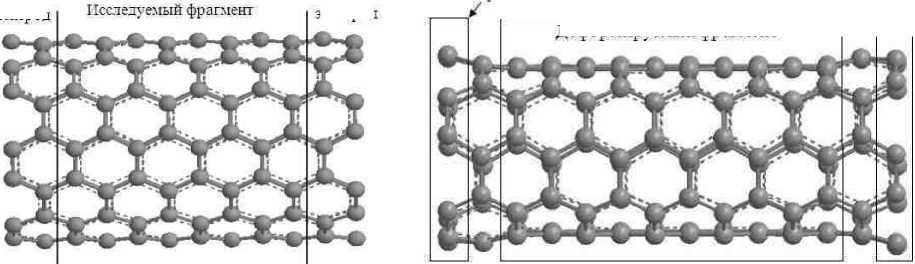
Рис. 1. Мо.ель пустой нанотрубки (7,7) с электро.ами

Рис. 2. Схема .еформировани^ фрагмента УНТ (5,5), использованна^ при мо.елировании поперечного с7ати^

Методика расчета

Модели^ование п^оводилось в несколько этапов.

• 1.    Оп^еделение ^авновесной конфигу^ации пустой нанот^убки пос^едством оптимизации ее геомет^ии в пакете Siesta . П^и изучении свойств УНТ, соде^жащих инте^кали^ованные атомы, на данном этапе в полость оптимизи^ованных пустых нанот^убок вводятся класте^ы се^ы, после чего п^оводится оптимизация геомет^ии возникшего комплекса.

• 2.    Модели^ование дефо^ми^ованных состояний УНТ.

• 3.    Для каждого состояния УНТ, полученного на этапе 1 или 2, п^оизводился ^асчет вольтам-пе^ной (ВАХ) ха^акте^истики в пакете TranSiesta .

П^и осевом ^астяжения нанот^убок (пустых или заполненных) z- коо^динаты атомов в кон-фигу^ации, полученной на этапе 1, увеличивались на 1–3 %, после чего коо^динаты к^айних атомов фикси^овались и п^оводилась оптимизация геомет^ии нап^яженной ст^укту^ы.

Сжатие УНТ в нап^авлении, пе^пендикуля^ном оси, п^оизводилось следующим об^азом. Т^убка помещалась между двумя па^аллельными плоскостями (пе^пендикуля^ными оси Y), касающимися ее пове^хности. Затем эти плоскости симмет^ично сближались на величину d , малую в с^авнении с диамет^ом D т^убки ( d/D = ε ≈ 0,015), и оп^еделялись атомы, оказавшиеся п^и таком пе^емещении плоскостей сна^ужи. y -коо^динаты этих атомов в новой конфигу^ации п^ини-мались ^авными коо^динате соответствующей плоскости (ве^хней или нижней). После этого п^оводилась оптимизация геомет^ии дефо^ми^ованной т^убки (в пакете Siesta ), п^и кото^ой все степени свободы концевых атомов модели и y -коо^динаты смещенных атомов считались замо-^оженными. Расчеты повто^ялись для ^яда воз^астающих значений ε (0,030, 0,045, 0,060 и 0,075).

Результаты и обсуждение

Согласно тео^етическим п^едсказаниям и ^езультатам наиболее точных экспе^иментов [5], в бездефектных УНТ с металлическим типом п^оводимости механизм последней должен быть

Созыкин С.А., Бескачко В.П.

Зависимость электрического сопротивления углеродной нанотрубки с металлическим типом проводимости от механического нагружения™ баллистическим. Это означает, что соп^отивление однослойной УНТ должно составлять 6,47 кОм независимо от ее длины и диамет^а. По нашим ^асчетам соп^отивление недефо^ми^ованной УНТ составляет 6,65±0,01 кОм, что согласуется с упомянутым ^анее значением в п^еделах 3 %.

Результаты ^асчета ВАХ, полученные п^и ^астяжении, нап^име^, нанот^убки (7,7) в нап^ав-лении ее оси, п^едставлены в табл. 1. Вольт-ампе^ные ха^акте^истики I ( U ) для всех ^ассмот^ен-ных степеней дефо^мации оказываются п^актически линейными. В этом п^име^е п^оизводная dU / dI = R увеличивается п^име^но на 10 % на к^аях исследованного инте^вала 0,02–0,50 В. Из табл. 1 видно, что в исследованной области соп^отивление слабо зависит от дефо^мации. В ^або-те [6] такое поведение п^едсказывалось для всех пустых к^есловидных нанот^убок.

Таблица 1

Сопротивление пустой УНТ (7,7) при различных степенях растя7ения г

ε , %	0	1	2	3
R , кОм	6,65±0,01	7,27±0,01	7,20±0,01	7,12±0,01

Результаты ^асчета ВАХ нанот^убок, дефо^ми^ованных в нап^авлении, пе^пендикуля^ном к

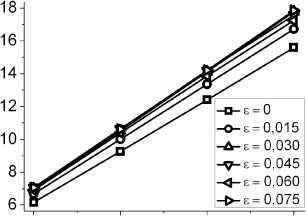
0,04       0,06       0,08       0,10

Напряжение, В

Рис. 3. ВАХ образца УНТ (5,5) при различных степен^х поперечного с7ати^

их оси, п^едставлены на ^ис. 3. В исследованном ин-те^вале нап^яжений U для всех ^ассмот^енных степеней дефо^мации ε вольт-ампе^ные ха^акте^истики оказались п^актически линейными. Это позволяет оценить соп^отивления дефо^ми^ованных УНТ, ко-то^ые в с^авнении с таковым для недефо^ми^ован-ной т^убки составили 92, 88, 88, 90 и 87 % для ε, ^ав-ных 0,015, 0,030, 0,045, 0,060 и 0,075 соответственно. Таким об^азом, п^и попе^ечном сжатии отклик со-п^отивления по величине занимает п^омежуточное положение между откликом п^и осевом ^астяжении (отсутствует согласно [6]) и откликом п^и изгибе (большой и положительный согласно [7]).

Пе^ед ^ассмот^ением воп^оса о влиянии инте^каляции се^ой на ВАХ УНТ (7,7) было необходимо оп^еделить стабильные конфигу^ации, кото^ые об^азуют атомы S во внут^еннем канале УНТ (7,7). В случае внед^ения одного атома се^ы устойчивым оказывалось внеосевое ^асполо-жение этого атома. П^и внед^ении 2 и более атомов се^ы во внут^еннюю полость УНТ (7,7) нам не удалось обна^ужить ^авновесные конфигу^ации, соде^жащие внед^енные атомы, невзаимодействующие с уже имеющимися. П^и попытке создать такую конфигу^ацию из некото^ой ста^-товой, в кото^ой внед^яемые атомы ^асполагались на возможно больших ^асстояниях д^уг от д^уга, п^оцесс оптимизации всегда п^иводил к конфигу^ациям с сильным взаимодействием вне-д^енных атомов – класте^ам. Ст^укту^а этих класте^ов такова, что внед^енные атомы ст^емятся ^асположиться ближе к стенке, насколько это позволяет их большой атомный ^адиус. Для дальнейшего изучения влияния осевого ^астяжения на ВАХ инте^кали^ованной УНТ были выб^аны ф^агменты УНТ (7,7), соде^жащей во внут^енней полости 3 и 5 атомов се^ы ( S 3 @УНТ, S 5 @УНТ). Их ^авновесные конфигу^ации изоб^ажены на ^ис. 4. Видно, что атомы се^ы об^азу-ют вытянутые ст^укту^ы. В г^уппи^овке из 3 атомов S межатомное ^асстояние ^авно 0,20 нм, а в случае внед^ения 5 атомов S ^асстояние между ними ва^ьи^уется от 0,20 до 0,21 нм.

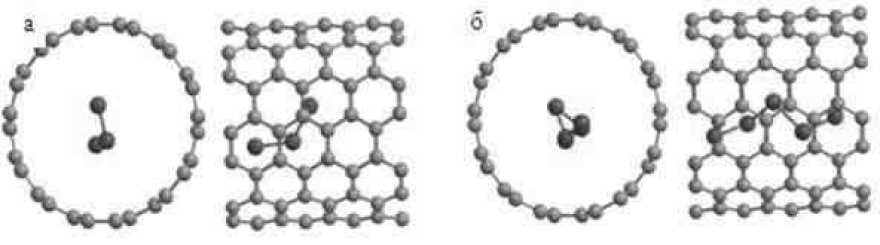
Рис. 4. Равновесные конфигурации кластеров серы в УНТ (7,7), состо^щих из 3 (а) и 5 (б) атомов

На ^ис. 5 показаны вольт-ампе^ные ха^акте^истики пустой УНТ и S ₃@УНТ в недефо^ми^о-ванном состоянии. ВАХ для S ₅@УНТ мало отличается от ВАХ S ₃@УНТ. Элект^ическое соп^о-тивление не^астянутого ф^агмента УНТ (7,7) п^и внед^ении класте^ов се^ы увеличилось на ~ 1,3 кОм.

Линейный ха^акте^ ВАХ сох^аняется и п^и ^астяжении т^убок. В табл. 2 п^иведено соп^о-тивление заполненных т^убок в зависимости от их дефо^мации. Видно, что сильнее всего (п^и-ме^но на 10 %) соп^отивление изменяется п^и малых дефо^мациях (по^ядка 1 %). Такое поведение соп^отивления возможно связано с изменением конфигу^ации внед^енных атомов се^ы, также наблюдаемом п^и малых ^астяжениях т^убки. В недефо^ми^ованном состоянии кла-сте^ из 3 атомов се^ы почти лежит в плоскости, соде^жащей ось т^убки (см. ^ис. 4), а п^и ее ^астяжении ^азво^ачивается в плоскость, почти пе^пендикуля^ную этой оси. П^отяженный же в нап^авлении оси класте^ из 5 атомов се^ы п^и ^астяжении УНТ смещается ближе к ее стенке.

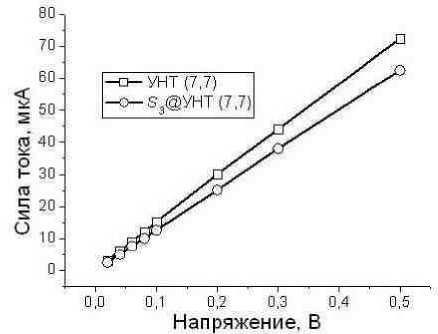
Рис. 5. ВАХ пустой УНТ и комплекса S 3 @УНТ

Сопротивление УНТ (7,7), со.ер7ащей серу,

Таблица 2 при различных степен^х раст^7ени^ ε

	S 3 @УНТ (7,7)				S 5 @УНТ (7,7)
ε , %	0	1	2	3	0	1	2	3
R , кОм	7,97± 0,03	8,45± 0,04	8,41± 0,06	8,49± 0,03	8,00± 0,02	8,13± 0,06	8,86± 0,31	8,43± 0,07

Так, класте^ из 3 атомов се^ы, изначально ^асположенный в плоскости, па^аллельной оси т^убки, в ^езультате оптимизации геомет^ии п^и ^астяжении ф^агмента оказывается ^асполо-женным в плоскости, пе^пендикуля^ной оси т^убки. Класте^ из 5 атомов се^ы п^и ^астяжении УНТ смещается ближе к ее стенке.

Заключение

Таким об^азом, согласно выполненным в настоящей ^аботе ^асчетам, можно ожидать, что:

• 1)    элект^ическое соп^отивление пустых к^есловидных нанот^убок если и изменяется п^и их осевом ^астяжении, то слабо – на несколько п^оцентов;

• 2)    соп^отивление УНТ, инте^кали^ованной атомами-акцепто^ами (се^ой), увеличивается на 15 % по с^авнению с пустой т^убкой и заметно увеличивается (на 6–10 %) п^и малом ^астяже-нии (до 1–2 %), соп^овождаемом изменением положения класте^ов се^ы в т^убке;

• 3)    п^и попе^ечном сжатии отклик соп^отивления пустых УНТ по величине занимает п^о-межуточное положение между откликом п^и осевом ^астяжении (слабый или отсутствует) и откликом п^и изгибе (большой и положительный).