Зависимость первичной стабильности дентального имплантата от направления окклюзионной нагрузки

В дентальной имплантологии хорошо известно, что косая нагрузка на имплантат опаснее вертикальной [4] (то же справедливо и для нативных зубов [12]). Имеется и ряд публикаций, касающихся расчета напряженно-деформированного состояния челюсти либо ее фрагментов с имплантатами под действием наклонной нагрузки [6‒9, 11, 13, 15, 17, 22]. Большинство из них посвящено остеоинтегрированным (сросшимся с костью) имплантам. Однако особое значение исследование системы «имплантат – челюсть» под действием косой нагрузки имеет при изучении первичной стабильности дентальных имплантатов, когда остеоинтеграция еще не произошла и на интерфейсе «кость ‒ имплант» нет сцепления [21, 14, 16‒20, 23]. Повреждающее воздействие чрезмерных нагрузок при этом связано с опасностью возникновения под их влиянием избыточных микродвижений (взаимных смещений ответных точек) на интерфейсе «кость – имплант», что ведет к нарушению процесса остеоинтеграции.

В работах [1, 2] на минимальной модели имплантатов в челюсти было рассмотрено влияние на первичную стабильность имплантата и микродвижения на интерфейсе характеристик резьбы при вертикальной нагрузке. В настоящей работе на той же модели изучается влияние на микроподвижность угла наклона нагрузки.

Постановка задачи

В качестве базового расчетного варианта был принят тот же, что и в [1, 2], но здесь сила P той же абсолютной величины образует с вертикалью угол α (α = 30°, 45° и 90°). Поэтому, в отличие от [1, 2], рассматриваемая задача не является осесимметричной (но все еще обладает одной плоскостью симметрии). Имея в виду возможную экспериментальную проверку, краевые условия поставили аналогично работе [3]: образец (цилиндр из кости с ввинченным имплантатом) как бы вставлен в жёсткий гладкий стакан (обойму), дно образца приклеено к стакану. Длина и диаметр обоймы приняты соответственно L = 30 мм, D = 20 мм [3]. Сводка всех использованных значений параметров базового расчетного варианта приведена ниже:

E , ГПа		ν		l , мм	d , мм	p , мм	h , мм	w , мм	L , мм	D , мм	P , Н	α, град
титан	кость	титан	кость
110	1	0,3	0,3	8	4	1	0,2	0,2	30	20	700	0, 90, 45, 30

Здесь E , ν – модуль Юнга и коэффициент Пуассона, l , d – габариты импланта (соответственно длина и диаметр); p , h , w – характеристики резьбы: соответственно шаг (период) p ( pitch ), глубина (высота) h и ширина основания зубца (нитки резьбы) w . Профиль резьбы был принят квадратным, поскольку в [1, 2] было показано, что в случае вертикальной нагрузки именно он давал минимальные микродвижения на интерфейсе. На интерфейсе «имплантат – кость» задавалось условие скольжения.

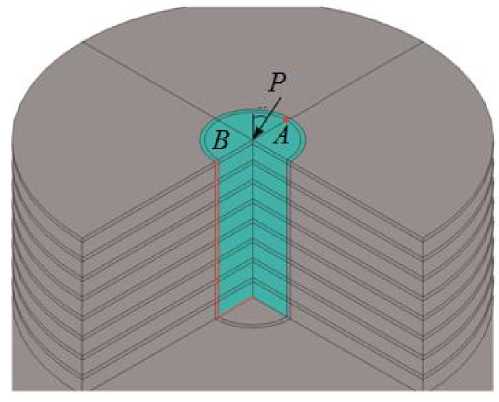
а

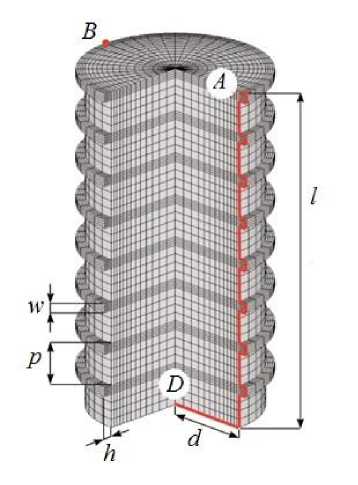
б

Рис. 1. Нагрузка на имплантат и точка максимальной микроподвижности A ( а ); общий вид импланта с четвертным вырезом ( б )

Расчёты выполнялись с использованием метода конечных элементов в программном комплексе ANSYS (версия 15.0). При построении конечно-элементной сетки использовались билинейные восьмиузловые конечные элементы в форме прямоугольного параллелепипеда. Вследствие наличия в задаче плоскости симметрии разбиению подлежала только часть (половина) модели, ограниченная этой плоскостью. Общее число элементов, использованных при разбиении, приблизительно равнялось 200 000. Для моделирования контакта между костью и имплантатом использовался метод штрафа.

Жесткость (модуль Юнга) имплантата на два порядка больше жесткости кости. Поэтому при действии на верхний торец имплантата горизонтальной силы имплантат практически как твердое тело наклоняется и поворачивается вокруг некоторой точки вблизи своего нижнего торца, называемой центром сопротивления [5]. При этом с одной (лицевой) стороны имплантат будет вдавливаться в кость (и здесь величины микродвижений будут минимальны – точка B ), а с другой (тыльной) – отстанет от кости – и здесь микродвижения будут максимальны (точка A ).

Наибольший интерес представляют места и величины максимальных микродвижений, поэтому в качестве фокусной точки были выбраны точка A (рис. 1), отвечающая максимуму микродвижений в определяемом ею поперечном сечении имплантата, и соответствующие этой точке вертикальное сечение и путь AD (рис. 1). Были проведены расчеты нормальной и тангенциальной компонент, а также модуля полного вектора микродвижений | u *| на интерфейсе вдоль пути AD и аналогичного пути BD .

Результаты расчетов и их обсуждение

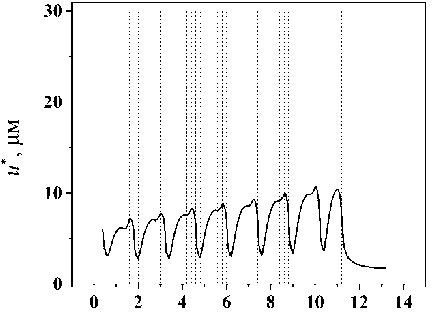
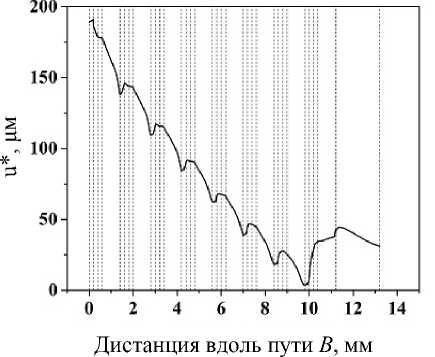
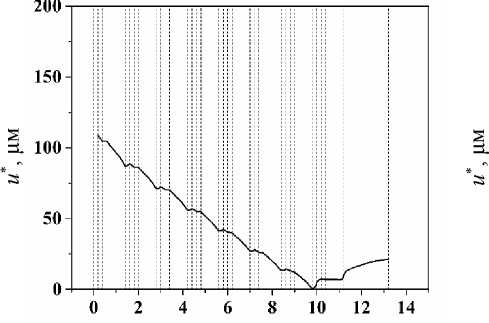
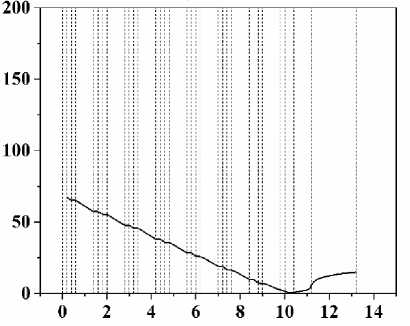
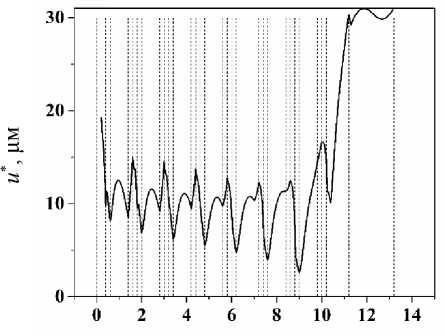
На рис. 2, а‒г представлены графики | u *| вдоль AD соответственно для α = 0°, 90°, 45°, 30°. На рис. 2, д для сравнения приведен график | u *| вдоль BD для α = 90°. Здесь первый штриховой столбик – верхняя грань зубца (нитки резьбы), второй столбик – боковая грань, третий – нижняя грань.

Прежде всего из сравнения рис. 2, б и 2, д видно, что микродвижения в точке B на порядок меньше, чем в точке A . Далее, из практики хорошо известно, что главные проблемы (вплоть до резорбции костной ткани) чаще всего возникают наверху имплантата, в «пришеечной» области. Полученные расчетные результаты могут служить возможным объяснением такого явления: из графиков 3, а‒г видно, что при вертикальной нагрузке максимальные перемещения возникают в апексной зоне, а при горизонтальной и косой нагрузке – наверху имплантата, при этом микродвижения при горизонтальной нагрузке на порядок больше, чем при вертикальном нагружении. Тот факт, что горизонтальные микродвижения больше вертикальных, отражает меньшую жесткость конструкции при горизонтальном нагружении в сравнении с вертикальным, что, в свою очередь, обусловлено геометрически.

Далее известно [14, 21], что лишь чрезмерная микроподвижность прямо связана с нарушением остеоинтеграции и формированием волокнистой инкапсуляции. Согласно [21] допустимый порог микродвижений лежит между 50 и 150 мкм: при | u *| < 50 мкм обеспечена остеоинтеграция, при | u *| > 150 мкм всегда происходит фиброинтеграция, при 50 мкм < | u *| < 150 мкм результат зависит от других (дополнительных) факторов. В наших расчетах значения микродвижений при изменении угла нагрузки от 0° (вертикальная) до 90° (горизонтальная) менялись больше чем на порядок (от 10‒12 до 180 мкм) и таким образом переходили из диапазона остеоинтеграции через промежуточную зону в область фиброинтеграции. Впрочем, надо оговориться, что принятые значения нагрузки близки к экстремальным [4] и, следовательно, в норме возникают редко. Считается, что типичные значения нагрузки P ~ 200 Н [4, 10], а при таких усилиях микродвижения будут примерно в 3,5 раза меньше, т.е. около 50 мкм, что, тем не менее, лежит на границе гарантированной остеоинтеграции.

Косая нагрузка представляет собой комбинацию вертикальной и горизонтальной нагрузок. Поскольку перемещения от вертикальных нагрузок на порядок меньше, чем от горизонтальных, при не слишком малых углах α ими можно пренебречь и учитывать лишь перемещения от горизонтальных усилий, которые равны P → = P sin α.

Дистанция вдоль пути A , мм а

б

Дистанция вдоль пути A , мм

в

Дистанция вдоль пути B , мм

г

Дистанция вдоль пути A , мм

д

Рис. 2. Изменение абсолютной величины микродвижений на интерфейсе «кость ‒ имплантат» вдоль пути AD при α = 0° ( а ), 90° ( б ), 45° ( в ), 30° ( г ), то же для BD α = 90° ( д ), w = 0,2 мм; h = 0,2 мм; p = 1,0 мм

При изменении силы P площадки контакта будут меняться, и таким образом задача нелинейна по P . Если эта нелинейность невелика, то график зависимости u (sin α) должен быть близок к прямой.

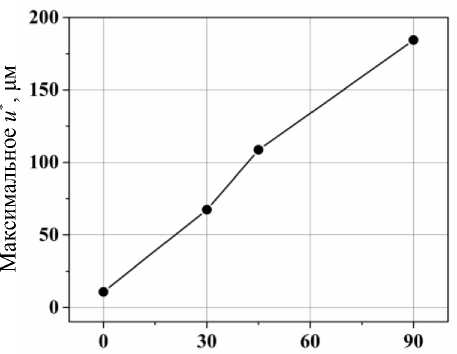
В таблице приведены значения максимальных относительных перемещений (микродвижений) на интерфейсе в зависимости от угла приложения нагрузки, а на рис. 3 ‒ те же данные показаны графически. Видно, что обе зависимости ( u (α), u (sin α)) существенно нелинейны, однако, в отличие от первой, график второй не имеет точек перегиба (сохраняет знак кривизны).

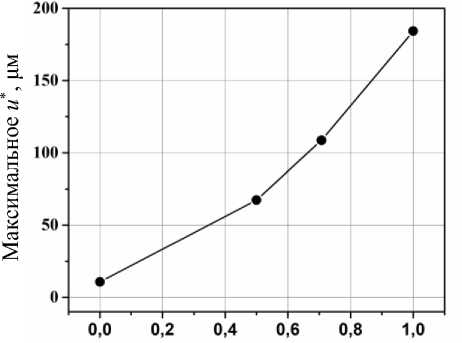
Максимальные микродвижения на интерфейсе «кость – имплант» при разных углах нагрузки

Направление нагрузки, град (угол α к вертикали)	sin α	Максимум перемещений, мкм	Положение максимума, (виток резьбы)
00	0	10,71	На последнем
30	0,5	67,36	На первом (шейка)
45	V2t2	108,65	На первом (шейка)
90	1	184,34	На первом (шейка)

α, град                                             sin α

Рис. 3. Зависимость максимальных значений микродвижений на интерфейсе «кость ‒ имплантат» от угла нагружения

Для того чтобы лучше понять полученный результат, дадим для смещений имплантата оценку на основе простейшей качественной плоской модели (рис. 4), в которой будем считать, что имплантат – жесткий гладкий стержень, а кость будем описывать как винклеровский слой.

Как уже было отмечено выше, при действии на верхний торец имплантата горизонтальной силы имплантат практически как твердое тело наклоняется и поворачивается вокруг некоторой точки вблизи своего нижнего торца, называемой центром сопротивления. Такой поворот описывается соотношением u(y) = k(y ‒ y0), где y – ордината, отсчитываемая от нижнего торца имплантата; u – смещение точек стержня по горизонтали (оси x); y0 – центр сопротивления; k – тангенс угла поворота. Две неизвестные y0 и k определяются из двух уравнений баланса: сил и моментов. Для расстояния между имплантатом и жесткой стенкой введем обозначение s D - d о =------.

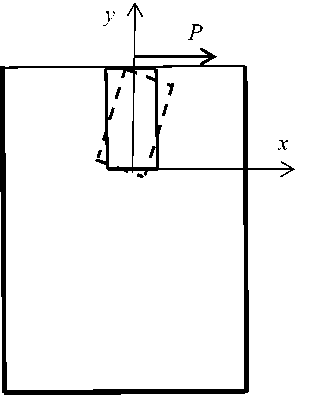
Рис. 4. Поворот имплантата под действием на его верхний торец горизонтальной силы P

Тогда уравнение баланса сил даст

l

l

l

P = J N ( y ) dy = J о Sdy = dE J k

y - y 0

δ

dl dy = kE- (y - y 0) dy =

δ0

_1t d I l = kE— -

-

5 ( 2

y_ol | = kE — 1 1 - 2 y 0 | , P = ⁰         25 I l )

2 P δ

kEdl ²

= 1 - 2 y = 1 - 2 y ₀.

Из уравнения баланса моментов

l

l

I 3

Pl = f N ( y ) ydy = kE- R y - y o ) ydy = kE- --y ⁰ 0                   ³ 00                      ³ ( ³

—

² 7

,

P = kE —

2   y ₀

— — ——

23 I 3 l

2Pδ 2 y 2

kEdl ² = 3 l " 3

- y 0 ,

2          1      2  1   1      2 P δ    6 P δ

1 -2yn =    yn, yn = -, P == -, k ==-,

0   3   0   0  3      3  3  3     PEdl2

ил и M         A  6P5 I/  11

umax = u (l) = k (y - y ) , = k (l - y0) =---7 l — = max              0мil       0м Edl21    3 i u || P, E, l, d, δ

(в конечно-элементной модели есть еще ν, габариты обоймы, параметры резьбы).

В силу линейности и из качественных соображений

P     5    15

u--, u ~ 5, u — —— u.

E        lEl

Далее по размерности d может войти единственным образом – в знаменатель, и с точностью до числового множителя получим, как и в (1),

P 5 1

u----=.

E l d Eld

Конечно, все эти качественные формулы малопригодны для оценки реальных величин интересующих параметров. Их ценность в том, что они приближенно (в тенденции), зато в явном виде показывают характер влияния некоторых основных параметров на нужные величины. Здесь оценки были проведены для перемещений и микродвижений, но то же можно сделать и для напряжений.

Отметим, что принятое для δ значение (δ = 8 мм) соответствует стабильности (перемещениям) в щечно-язычном направлении либо перемещениям одиночного импланта в медиально-латеральном направлении в отсутствие смежных зубов; при проведении подобных расчетов и оценок на практике принимаемые значения параметров должны отвечать конкретной ситуации.

Выводы

Изменение направления действия силы на имплантат от вертикального к горизонтальному в отсутствие сцепления на интерфейсе «кость – имплантат» (при немедленном нагружении, при неполной остеоинтеграции) приводит к драматическому – больше чем на порядок – росту микродвижений (взаимных смещений ответных точек) на интерфейсе и перемещению их максимума с апекса на шейку имплантата. Если действующие при этом окклюзионные нагрузки достаточно велики, существует опасность возникновения на интерфейсе чрезмерных микродвижений, что может привести к нарушению остеоинтеграции, в особенности в пришеечной зоне импланта.

Благодарности

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А17-117021310386-3) и при частичной поддержке грантов РФФИ №17-08-01579 и № 17-08-01312.