«Жанармай – қазандықтағы бу қысымы» каналы бойынша бу өндіру қазандығының беріліс функциясы

ӘОЖ 65.011.56                           

Кіріспе

Қазіргі заманғы энергетика негізін ірі жылу электр станциялары (ЖЭО), өндірістік жылыту қазандықтары, өндірістерді жылу-мен жабдықтау жүйелері, әр түрлі мақсат-тағы тоңазытқыш қондырғылар, кептіру қондырғылары және т.б. құрайды. Солардың ішінде қазандық қондырғысы жылу станциясының негізгі буындарының бірі болып табылады, оның сенімді және тиімді жұмысы тұтастай жылу-энергетикалық жүйелердің тиімділігін айқындайды деседе болады. Жылу қазандықтарын пайдалану барысында әдетте біраз мәселелер туындайды. Мысалға, механикалық тұрғыда – қазандық элемент- терінің механикалық зақымданулары [1], экологиялық тұрғыда - атмосфераға кететін отынның жану өнімдеріндегі (түтін газдары) экологиялық қауіпті заттар концентрациясын төмендету проблемалары [2]. Осындай олқылықтарды мейлінше азайту барысында әдетте автоматтаныдру мәселесі көтеріледі [3].

Әдетте бу қазандығында өтетін процесстерді автоматты реттеу үшін басқарылатын обьектілердің (бу қазаны) математика-лылқ модельдері белгілі болуы қажет. Практикалық тұрғыда обьектілердің мате-матикалық модельдерін алудың бірден бір жолы – тәжрибелік жолмен алынған екпін қисығын өңдеу. Өңдеудің әдетте түрлі тә- сілдері бар, дегенімен дәлдігі жоғары тәсілдің бірі – М.П. Симою және Е.П. Стефани тәсілі. Кейде бұл тәсілді «аудандар тәсілі» депте атайды [4,5].

Зерттеу материалдары мен әдістері

Зерттелетін обьект ретінде бу өндіру қазандығы қарастырылады.

Мақаланың негізгі мақсаты, бу қысымы мен қазандыққа берелетін жанармай мөлшерінің араларындағы тәжрибелік тәуелділікті өңдеу арқылы, «жанармай – қазандықтағы бу қысымы» каналы бойын- ша бу қазандығының математика-лық мо-дельін айқындау.

Зерттеу тәсілі – тәжрибелік екпін қи-сығын М.П. Симою және Е.П. Стефани тәсілі арқылы өңдеу

Нәтижелер және оларды талқылау

Обьектінің математикалық моделін обьектінің кірістік және шығыстық шамаларының араларындағы тәжрибелік жолмен алынған сипаттамаға сүйене отырып анықтауға болады. Осындай тәжрибелік сипаттаманың бірі [6] еңбекте келтірілген (1 кесте).

1-кесте. Тәжрибелік мәліметтердің орта мәндері. μ, % - реттеуші органның ашылу дәрежесі, р с – қысым (обьектінің шығыстық шамасы), Ϭ – шығыстық шаманың өлшемсіз түрдегі ауытқуы

μ, %	10	10	10	10	10	10	10	10	10	10	10
р с , бар	0	0,29	0,68	0,96	1,17	1,3	1,4	1,43	1,48	1,5	1,56
t, мин	0	2	4	6	8	10	12	14	16	18	20
a = -^Pc- P c ( да )	0	0,186	0,436	0,616	0,75	0,834	0,9	0,917	0,95	0,96	1,0

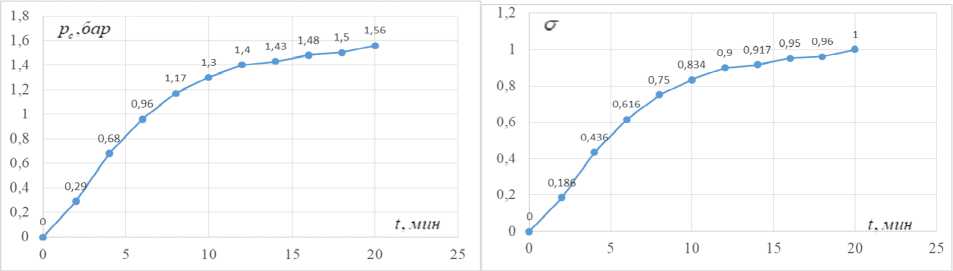
Кестелік мәліметтерге сүйеніп, екпін қисығын тұрғызамыз (1 сурет)

б

1 cурет. а -тәжрибелік екпін қисығы, б - салыстырмалы бірліктегі екпін қисығы

Полиномдар коэффициенттерінің оң мәндерін қанағаттандыратындай беріліс функ- циясының макеті келесі түрде аламыз w 0 (s ) =

b 1 5 + 1

а 2 s ² + а 1 5 + 1

Беріліс функциясының алымындағы және бөліміндегі полиномдардың коэффициенттері жалпы жағдайда келесі теңдеулер жүйесінен табылады [7]

« , = F . + b , + Y b . F . - j j - i                            (2)

Біздің жағдайда бұл теңдеулер жүйесі мынаған тең а1 = F1 + b1

а 2 = ^F 2 ^{+ b} 1 ^F 1

0 = F 3 + b 1 F₂

Ал интегралдық аудандар Fi келесі фомуладан анықталады [7]

да

F = F i f (1 - a )

( - ө ) i ^{- 1} + ( - ө )^{1 - 2} ₊ ^—3 Қ - ₃ - 1^{( - Ө ) J} ( i - 1)!   ( i - 2)!    :j : 0   F^ j j!

dӨ

Біздің жағдайда белгісіз коэффициенттер саны үшке тең, сол себепті есептелетін интегралдық аудандар саны да үшке тең болуы қажет. Практикалық тұрғыда (4)

• — = A 1 I E [ 1 - ^CT ( i A t ) ] - 0.5 [ 1 - ^ (0) ] )

• ¹       I t0

n интегралды алу мүмкін емес, сондықтан ин- тегралды жуықтап қосындымен алмастырады да, келесі түрде жазады i=0

n

— з = F ₁ ³ A Ө ^ ^ [ 1 - a( i A t ) ] 1 - 2Ө( i A t ) + 2 Ө ²( i A t )

-

0.5 [ 1 - а (0) ] >

I i = 0

мұнда Δt – уақыт интервалы ( Δt=2 мин ), θ(iΔt) – cалыстырмалы уақыт

І A t

Ө( iAt) = —

Есептеу кезеңдері :

2-кестеде F 1 ауданын есептеуге арналған мәліметтер келтірілген.

2-кесте. F 1 ауданын есептеуге арналған мәліметтер

t	0	2	4	6	8	10	12	14	16	18	20	∑
р	0	0,29	0,68	0,96	1,17	1,3	1,4	1,43	1,48	1,5	1,56
cr( i A t )	0	0,186	0,436	0,616	0,75	0,834	0,9	0,917	0,95	0,96	1,0
1 - c t( i A t )	1	0,814	0,564	0,384	0,25	0,166	0,1	0,083	0,05	0,04	0	3,451

2 кестедегі мәліметті пайдалана отырып, (5) формуладан F1 ауданның мәнін есептеп табамыз:    F1 = 5,9;    Қалған аудандарды есептеу үшін 3 кестені құамыз

3 кесте. F 2 және F 3 аудандарын есептеу үшін қажеті мәліметтер

1 - < r ( i A t )	1	0,814	0,564	0,384	0,25	0,166	0,1	0,083	0,05	0,04	0
Ө ( i A t )	0	0,34	0,677	1,017	1,356	1,695	2,034	2,373	2,712	3,051	3,39
Ө 2( i A t )	0	0,116	0,458	1,034	1,839	2,873	4,137	5,631	7,355	9,309	11,5
1 - Ө ( i A t )	1	0,66	0,323	-0,02	-0,36	-0,69	-1,03	-1,37	-1,71	-2,05	-2,39

Есептеу нәтижелері төменде	Беріліс коэффициенті k 0 [6] еңбекте
келтірілген:      F 2 = 7,35;     F 3 = -3,48;	есептелген, есептеу нәтижесі бойынша k 0 =
Аудандардың мәндерін (3) теңдеу	1,6 тең. Беріліс коэффициентін есепке ала
жүйесіне қойып, полиномдар коэффициент-	отырып, бу қазандығының «жанармай-бу
терін анықтаймыз. Есептеу нәтижелері:	қысымы» каналы бойынша беріліс функция-
b 1 =0,473;   а 1 =6,37;   а 2 =10,12;	сын былайша жазамыз
	0,76 s + 1,6
W ) ( P ) = k 0    2 1       , а 2 5 + а 1 s + 1	= 10,12 s 2 + 6,37 s + 1                              (7)

Бұл жағдайда бу қазандығы тұрақты коэффициентті екінші ретті сызықты дифференциал теңдеумен өрнектеледі

10,12 d ² р\ (t ) + 6,37 d^ + р_с (t ) = 0,76 d^ ( t ) + 1,6 ^ ( t )                     (8)

• , dt ²        , dt ^с , dt ,

• 3    суретте Matlab(Simulink) модельдеу ортасының стандартты блогын Transfer Function қолдану арқылы өтпелі сипаттама тұрғызылған [8].

  
  
  

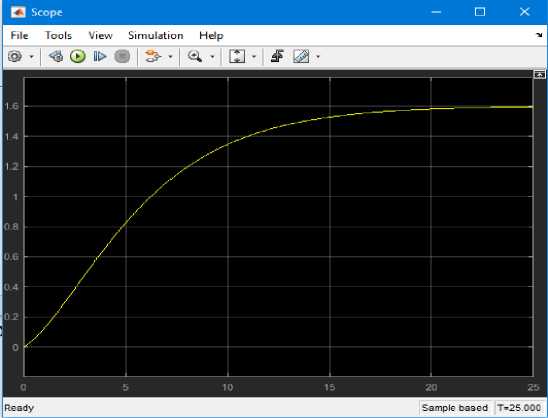
3 сурет. «Жанармай-бу қысым» каналы бойынша тұрғызылған екпін қисығы

• 3    суреттен байқайтынымыз, алынған математикалық модель тәжрибелік жолмен алынған сипаттаманы адекватты сипаттайты.

Қорытынды

• 1.    Бу қазандығының «жанармай-бу қысымы» каналы бойынша алынған тәжри-белік деректерді пайдалана отырып, бу қазандығының математикалық модельі айқындалды. Бу қазандығы екінші ретті сызықты дифференциал теңдеуімен сипатталады.

• 2.    Бу қазандығының өтпелі сипаттамасы Matlab(Simulink) модельдеу ортасының стандартты блогын Transfer Function қолдану арқылы тұрғызылды. Модельдеу нәтижесі матема-тикалық модельдің бу қазандығында өтетін процессті адекватты сипаттайтынын көрсетті.

• 3.    Мақалады келтірілген нәтижелер болашақта бу өндіру процесстерін автоматтандыруда қолданыс табады

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

• 1.    Костюк А.Г., Куменко А.И., Некрасов А.Л., Калинин С.В., Медведев С.В. Эксперимен-

  тальный анализ пульсаций давления в пароподводящих органах турбоагрегата.- // Теплоэнергетика , 2000.- № 6.- С. 50-57.

• 2.    Росляков П.В., Закиров И.А., Егорова Л.Е., Ионкин И.Л., Чадаев А.В., Райсфельд А.А. Система непрерывного контроля и регулирования процесса горения и вредных выбросов в атмосферу.- // Теплоэнергетика , 2000.- № 6.- С. 35-40.

• 3.    Голдобин Ю.М., Павлюк Е.Ю. Автоматизация теплоэнергетических установок : учеб. пособие /.— Екатеринбург : УрФУ, 2017.— 186 с.

• 4.    Шишкин О. П., Парфенов А. Н. Основы автоматики и автоматизация производственных процессов. Учебник для нефт. вузов и фак. – М.: Недра, 1965. - 340 с.

• 5.    Стефани Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. 2-е изд., – М.: Энергия, 1972. – 376 с.

• 6.    Пиотровский Д. Л. и др. Моделирование процесса стабилизации давления пара в паровом котле.- //КубГАУ.- №92(08).- 2013.- С. 237-239.

• 7.    Мартыненко И.И. Проектирование, монтаж и эксплуатация систем автоматики.- М.: «Колос», 1981.-304 с.

• 8.    Дьяков В.П. MATLAB. Полный самоучитель.-М.: ДМК Пресс, 2012.-768 с.