Жизненные задачи как средство изучения нового материала при обучении геометрии в средней школе

Бюллетень науки и практики / Bulletin of Science and Practice Т. 9. №3. 2023

УДК 371.3:513                                    

Постановка проблемы перед изучением нового материала по геометрии в средней школе вносит осознанность в его изучение учащимися, позволяет добиться повышение качества математической подготовки школьников. Изучение этого вопроса привлекает внимание методистов всего мира. В государственном предметном стандарте по математике в школах Киргизской Республики (5–9 классы) сформулированы следующие требования к уровню подготовки выпускников, которые принято использовать для характеристики уровня математической компетентности: использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• –    практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;

• –    построения и исследования простейших математических моделей;

• –    описания и исследования с помощью функций реальных зависимостей, представления их графически;

• –    интерпретации графиков реальных процессов;

• –    решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа;

• –    анализа реальных числовых данных, представленных в виде диаграмм, графиков, анализа информации статистического характера;

• –    исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур; вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства [2].

Целью изучения математики в 7–9 классах является развитие вычислительных и алгебраических умений, усвоение функции, аппарата уравнений и неравенств как основного средств математического моделирования прикладных задач, систематическое изучение геометрических фигур на плоскости и в пространстве, развитие логического мышления и подготовка учащихся к изучения смежных дисциплин. Перед учащимся ставится какая-либо практическая задача, разрешение которой возможно лишь с помощью определенной математической закономерности, которую предстоит изучить. Здесь сама задача указывает школьнику на необходимость изучения нового теоретического материала. Жизненные задачи для постановки проблемы перед изучением нового материала могут быть использованы на всех этапах школьного курса математики.

В средней школе при изучении математики поставлено задачи, подводящих учащихся к необходимости изучении нового материала:

• 1.    Когнитивная. Учащийся понимают закономерности построения числовых систем (натуральные, целые, рациональные, действительные) и используют математический язык как инструмент познания, исследования и общения;

• 2.    Поведенческая. Учащийся владеют математическими знаниями, умениями и компетенциями необходимыми для их применения в практической деятельности, изучения других предметов, а также для продолжения математического образования в последующих классах;

• 3.    Ценностная. Учащийся мотивированы к совершенствованию своих математических познаний в приобретении вычислительных, логических и других качеств, способны к анализу, оценке своего результата и вполне осознают погрешности математических измерений [2].

Ученику шестикласснику, очень трудно освоить алгебраические выражения, если дать ему без предварительных жизненных задач, позволяющих уяснить сущность изучаемых понятий. Поэтому изучение алгебраических выражений мы считаем целесообразным начинать с решением системы жизненных задач. В этом случае с жизненным содержанием органически переплетаются с излагаемым новым материалом, составляя его неотделимую часть.

Например, перед объяснением учащимся темы «Решение квадратных уравнений» целесообразно поставить задачу; «Тело брошено вертикально вверх со скоростью 30 м/сек. Через сколько времени оно будет на высоте

Н=40 м (g=10 м/сек² )? При решении этой жизненной задачи с физическим содержанием учащиеся на основе своих знаний из курса физики пользуются законом движения тела, брошенного вертикально вверх: Н = V₀t — gt .

После подстановки и преобразований получается уравнение t2 — 6t + 8 = 0 , к объяснению приемов решения которого учитель и приступает [1].

Перед выводом формулы объема цилиндра учащимся предварительно предлагается задача: «Имеется моток медной проволоки весом 50 кг. Определите длину проволоки в мотке, если ее диаметр равен 2 мм».

В ряде случаев приходится по части круга — сегменту определить радиус, диаметр, длину окружности, площадь круга. С жизненными задачами мы сталкиваемся, когда часть круга закопана в земле, закрыта водой, защитным кожухом и т.д. такие задачи целесообразно предложить учащимся перед изучением темы «Метрические соотношения в круге» [4].

В обучении темы окружности, выводом формулы длины окружности, учащимся предлагается задача: «Барабан лебедки, диаметр которого 300 мм, сделал 10 оборотов. На сколько при этом поднялся груз?».

В VII классе по геометрии ознакомлением с формулой площади круга учащимся предлагаем задачу: «Длина стрелы башенного крана равна 10 м. Определить площадь участка, который может обслуживать кран, не передвигаясь (площадь, занимаемую самим краном, в задаче не учитывать, так как она невелика)».

При изучении признаков равенства треугольников учащимся для решения ставится задача на определение расстояния до недоступной точки; знакомству их с тригонометрическими функциями предпосылается решение задач на вычисление высоты предметов без их непосредственного измерения [3].

Перед ознакомлением учащихся со способом определения величины угла по данному числовому значению данной тригонометрической функции целесообразно предложить задачу: «Пользуясь одной мерной лентой, как нужно определить угол наклона подпорки телеграфного столба к поверхности земли (саманной подпорки к стене зернохранилища, троллейбусной вилки — к плоскости его крыши и т. д.)» или «Надпись 5/1000 на столбе около железнодорожного пути означает, что на протяжении 1 км путь поднимается в гору на 5 м. Найти угол наклона пути к горизонту».

Жизненные задачи, решаемых на уроке, производственная характеристика того или иного объекта или орудия труда преобладает над их математическим содержанием.

Например: «На Рисунке изображен фрезер. Он служит для резания металла. Фрезер надевается на ось (шпиндель) машины на шпонке и приводится во вращательное движение по направлению движения часовой стрелки, причем острыми краями (зубцами) срезывается металл. Расстояние от зубца к зубу по окружности называется шагом; обозначим его через t.

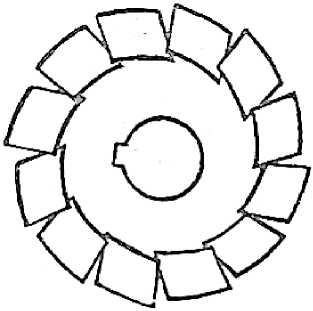
Рисунок.

Если умножить шаг на число зубцов, то получим, очевидно, окружность фрезы. Обозначим длину окружности фрезы через С, а ее диаметр через d. Число зубцов фрезы обозначим через z, тогда с = zt; d = -; d = —. ft         ft

• 1.    Фреза должна иметь 30 зубцов; шаг ее зубцов равен 12 мм. Каков должен быть диаметр фрезы?

• 2.    Чему равно число зубцов фрезы, если диаметр ее равен 40 мм, а шаг t = 7,5 мм?

Решение: d = — = ³⁰¹² « 115 (мм). ft      3,14

Решение: z = — = ^{40 3,14} ~ 17 (зубцов)». ft        7,5

Как видно математическое решение задачи слишком просто, оно сводится к нахождению числового значения выражения по подстановке.

Таким образом, во всех жизненных задачах используемые формулы интерпретированы на частных примерах с нахождением числовых значений алгебраических выражений при определенных численных значениях отдельных букв.

Из всего сказанного следует, что:

Бюллетень науки и практики / Bulletin of Science and Practice Т. 9. №3. 2023

• -    использование задач с жизненным содержанием в системе учебно-воспитательной работы в средней школе при изучении геометрии, зачастую носит формирующий характер математических предметных компетенций, и в том числе ключевых компетенций;

• -    цели и требования государственного образовательного стандарта школьного общего образования и предметных стандартов по «математике» Киргизской Республики усилить содержательно-прикладное значение курса математики и формирование ключевых компетенций школьников.