Актуальность использования задач на готовых чертежах при обучении учащихся 7-го класса анализу условия планиметрических задач

Задачи являются важной частью курса математики, и особенно геометрии. Роль задач трудно переоценить. При решении геометрических задач не только проявляются математические знания и умения учащихся, но и задействуется большое количество универсальных учебных действий: умение логически рассуждать, строить высказывания, выражать свои мысли, структурировать информацию, вычленять проблему, проводить рефлексию.

Однако решение задач, условие которых требует преобразования, построения чертежа, где учащимся необходимо самостоятельно провести поиск решения, найти промежуточные данные и включить их в систему исходных данных, представляет для учащихся большую трудность. Успешно решаются лишь типовые простейшие задачи на вычисление, где ученикам в явном виде нужно применить одну формулу (например, найти площадь треугольника или параллелограмма, если известны высота и основание). Это подтверждают результаты ОГЭ и ЕГЭ по профильной и базовой математике, представленные на официальном сайте Федерального института педагогических измерений за 2018–2020 г. Эксперты ФИПИ отмечают, что низкие результаты выполнения геометрических задач свидетель- ствуют о концептуальных недостатках в обучении геометрии, о необходимости пересмотра традиционных систем обучения с существенным акцентом на развитие умений смыслового чтения условия задач, геометрической интуиции и наглядных геометрических представлений [9].

Одной из основных сложностей для учащихся при решении задач по геометрии является построение чертежа. На эту трудность указывали в своих работах многие методисты, в том числе А.М. Астряб, В.А. Гусев, Г.И. Саранцев [3]. Особенностью геометрического чертежа является его двоякая роль: с одной стороны, без тщательного анализа условия невозможно изобразить правильные связи на чертеже, с другой – только хорошо проанализированный чертеж дает успешный анализ условия задачи.

Проведенный нами констатирующий эксперимент среди учащихся 7–9-х классов Горо-дищенской МБОУ СОШ № 1 (127 чел.) показывает, что учащиеся не умеют преобразовать чертеж, они представляют чертеж как самостоятельный объект без связи и исследования задачной ситуации. В современной школе исследовательская деятельность учащихся присутствует формально, фактически же не осуществляется совсем. Формирование приемов анализа и преобразования имеющегося чертежа у школьников, как правило, идет стихийно, в отрыве от преобразования заданной ситуации, не планируется учителем [5].

На наш взгляд, первоисточник проблемы решения геометрических задач – это непосредственное построение чертежа к задаче. Сам процесс построения даже элементарных геометрических объектов вызывает затруднения у учащихся. Очень часто рисунок ученика к задаче не только не помогает, но еще больше запутывает и усложняет работу над задачей. Уже в 7-м классе у учащихся начинает формироваться «искаженный» принцип зрелого геометра: «Геометрия – это искусство делать правильные выводы по неправильным чертежам». Однако для учеников 7–8-х классов в обучении геометрии (как и в содержании учебного пособия для учащихся) основополагающим должен быть другой принцип: «Геометрия – это искусство выдвигать гипотезы решения задачи по нескольким правильным чертежам, далее опровергать или доказывать их».

Результатом теоретического анализа стал вывод о том, что умение строить чертеж яв-

ляется многокомпонентным и включает в себя совокупность умений:

• –    строить базовые фигуры;

• –    выделять элементы фигуры;

• –    выделять порядок построения при комбинации фигур (трапеция, вписанная в окружность, с какой фигуры начинать построение);

• –    преобразовывать чертеж;

• –    выделять на чертеже условие задачи и считывать информацию с чертежа.

Однако, на наш взгляд, весь комплекс умений, связанных с чертежом, базируется на главном, первоочередном умении, обладающем высокой степенью обобщенности – умении строить чертеж по условию данной задачи. В ходе экспериментальной работы мы установили, что формирование этого умения следует начинать с обучения построению так называемых точных чертежей. Под точным чертежом мы понимаем точное построение данных фигур и их свойств на плоскости с помощью различных инструментов (циркуля, линейки с делениями, транспортира, угольника и других шаблонов), при этом алгоритм построения не имеет значения. Процесс формирования данного умения, как и любого другого, имеет свою логику: начинается с начального уровня, менее совершенного, и движется к другому – более совершенному. На каждом этапе формирование умения достигается целесообразным сочетанием задач на вычисление и доказательство. Совершенствование умения строить точный чертеж, накопление опыта в построении точных чертежей у учащегося приводят к качественному переходу на уровень понятийного мышления, когда он начнет делать рисунки, которые будут правильно изображать все свойства геометрической фигуры без точных измерений.

Теоретическим путем мы пришли к выводу, что обучение учащихся построению чертежей по условию задачи невозможно без работы на готовых чертежах, когда учащиеся видят идеальные модели того, что должно стать результатом их работы при самостоятельном построении. К тому же работа на готовых чертежах экономит время и позволяет показать большее количество вариантов чертежей или варианты их преобразований. Здесь и кроется еще одна проблема – практически полное отсутствие методических пособий для учителей и учащихся, предусматривающих выполнение заданий на готовых чертежах. На сегодняшний день учитель может найти задачи на готовых чертежах или в сети Интернет, которые выполнены его коллегами, например в рамках каких-нибудь конкурсов, или в методических пособиях для подготовки к ОГЭ и ЕГЭ. Но задачи в этих пособиях направлены на отработку теоретических знаний, конкретной темы, подразумевая, что учащиеся уже умеют работать с чертежами: читать чертеж, использовать геометрическую символику. В сборниках задач на готовых чертежах нет заданий, которые учат работать с этими чертежами: выделять фигуру и элементы фигуры; отмечать равные элементы, отношение отрезков. Таким образом, при изучении геометрии в 7-м классе необходима целенаправленная деятельность по формированию навыков для работы с чертежом:

• –    равные стороны отмечать одинаковыми штрихами;

• –    равные углы – равными дугами;

• –    вершины многоугольника указывать точками;

• –    невидимые линии (стороны) обозначать пунктиром;

• –    использовать штриховку, когда речь идет о периметре или площади фигуры;

• –    указывать общепринятые обозначения для геометрических объектов (например, для прямого угла использовать специальный знак);

• –    в задачах на вычисление обязательно отображать все количественные данные и то, что требуется найти (на первых этапах обучения анализу условия планиметрических задач можно использовать разные цвета: зеленым цветом выделять элементы, значения которых известны; красным – то, что неизвестно и требуется найти; синим – то, что неизвестно, но будет получено в ходе промежуточных вычислений);

  – отражать на чертеже выводы, полученные из первичного анализа данных условия (например, если в условии задана медиана треугольника, значит, сразу следует отметить одинаковыми штрихами равные части стороны, на которую опущена медиана; если в задаче говорится о биссектрисе – отметить равные углы).

Нами определены типы задач на готовых чертежах к первым темам курса геометрии, нацеленных на обучение учащихся анализировать условие задачи и соответственно строить чертеж: задачи на выделение объекта и записи его названия; задачи на комбинацию фигур; задачи на нетипичное расположение фигуры; задачи с недостающими данными; задачи без сформулированного вопроса. Рассмотрим примеры таких задач.

При изучении темы «Углы» в школьной жит только один угол, то учащиеся его назы- практике не акцентируется внимание на умении давать названия углам по вершинам. По умолчанию считается, что ученики умеют это делать. Однако, как показывает практика, это совсем не так. Если на рисунке вершину содер- вают правильно, если какая-то точка является вершиной нескольких углов, то ученики допускают ошибки даже в старших классах. Формировать умение называть углы необходимо в 7-м классе (рис. 1–3).

Рис. 1

Задания к рис. 1:

• 1)    перечислите все углы, изображенные на рис. 1;

• 2)    выберите верные утверждения, соответствующие рис. 1:

• а)    ےABC – тупой угол;

• б)    ےMBC – тупой угол;

• в)    ےАВM – развернутый угол;

• г)    ےBCM – острый угол;

• д)    ےBMC – тупой угол.

  

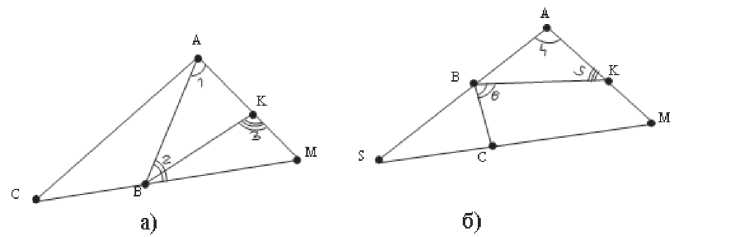
  Рис. 2

  
  

Задания к рис. 2а:

• 1)    запишите названия отмеченных углов (по трем вершинам) на рис. 2а;

• 2)    отметьте углы на рисунке 2а: ےACM, ےBKA, ےCAM.

• 3)    выберите неверное утверждение в соответствии с рис. 2а:

• а)    ےBAK < ےCAK;

• б)    ےCBA > ےCBK;

• в)    ےCBA + ےABM = ےCBM;

• г)    ےCAB + ےBAK = ےCAK.

Задания к рис. 2б:

• 1)    запишите названия отмеченных углов (по трем вершинам) на рис. 2б;

• 2)    отметьте углы на рис. 2б: ےABC, ےCMK, ےBCS;

• 3)    выберите верные утверждения в соответствии с рисунком 2б:

• а)    ےABK < ےABC;

• б)    ےAKB > ےAKM;

• в)    ےSBC + ےKBC = ےSBK;

• г)    ےCKB + ےKBA = ےCBA.

  

  Рис. 3

  Задания к рис. 3а и 3б:

  1) назовите пары смежных углов, которые есть на рисунке 3а;

  2) используя рис. 3б, назовите углы смежные с перечисленными ниже: а) ےEMK;

  
  

  б)ےSEM; в)ےBMA.

  
  

При изучении равнобедренного треугольника и его свойств предполагается, что ученики выучили определение и смогут без труда на чертеже определить основание, боковые стороны, прилежащие углы. И это действительно так, потому что, решая задачу о равнобедренном треугольнике, и ученики, и учителя изображают самый типичный случай, когда основанием является сторона, на которой треугольник стоит, так вырабатывается стереотип. При другом расположении равнобедренного треугольника, когда он является частью других фигур, ученики не могут правильно определить основание, а соответственно, выделить равные углы. Для формирования правильных представлений о равнобедренном треугольнике необходимо предложить учащимся как можно больше чертежей с различным расположением сторон с соответствующими заданиями. Сначала предлагаем треугольники, на которых выделены равные боковые стороны с соответствующими вопросами:

• •    Какие стороны являются боковыми?

• •    Какая сторона является основанием?

• •    Какой угол является противолежащим основанию?

• •    Какие углы являются прилежащими основанию? (сразу отмечать равные углы одинаковыми дугами).

После того как ученики рассмотрели как минимум 5–6 видов треугольников, предлагаем им новые комбинации, но с уже отмеченными равными углами и, соответственно, вопросами:

• •    Какая сторона является основанием?

• •    Какие стороны являются боковыми?

• •    Какой угол является противолежащим основанию?

• •    Какие углы являются прилежащими основанию?

Обязательно нужно включать в работу чертежи с комбинациями фигур, когда треугольник существует не сам по себе, а является частью чего-либо. Так, на рис. 3в ученики должны увидеть все равнобедренные треугольники, для каждого из них перечислить основные элементы (вопросы выше).

Аналогичная работа необходима при изучении прямоугольного треугольника, т. к. при его нестандартном расположении, когда он является частью другой фигуры, учащиеся даже в старших классах путают катеты и гипотенузу, неправильно определяют прилежащий и противолежащий угол. С первых уроков также необходимо формировать умение составлять условие задачи по чертежу, формулировать вопрос к задаче, конструировать обратные задачи (рис. 4).

На начальном этапе учащиеся решают систему задач на готовых чертежах, где отмечены все данные и поставлен вопрос. Цель решения таких заданий – научить считывать условие, правильно интерпретировать геометрическую символику, ведь зачастую ученики вообще не обращают на нее внимание. Например, на рис. 4 ученикам необходимо увидеть, что отрезок ОК является биссектрисой угла BOM . После решения задачи целесообразно составить обратную задачу (например: угол AOM

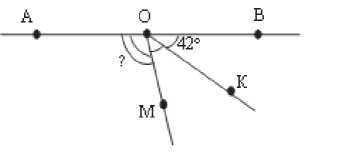
Рис. 4

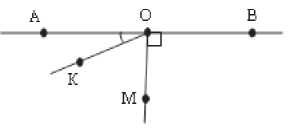
Рис. 5

равен 96°, OK – биссектриса угла BOM , найдите угол BOK ).

После проведенной работы целесообразно предложить ученикам систему задач без вопросов, которые учащиеся должны сформулировать самостоятельно. При этом они фактически отвечают на вопрос синтеза «Зная то и то, что я могу найти?». Ведь вопрос ставится не бездумно, для этого ученик уже должен мысленно проанализировать условие. Например, на рис. 5 большинство учеников попросит найти угол МОК , но необходимо побуждать учащихся рассматривать различные варианты, например можно найти угол BОК. После решения задачи снова формулируем и решаем обратную (угол BOK равен 150°, а угол BOM равен 90°, найдите угол AOK ) . Естественно, что такая работа не должна быть ситуативной, она должна быть регулярной с подобранной системой задач.

Из всего вышесказанного следует, что задачи на готовых чертежах обеспечат обучение учащихся анализу условия планиметрических задач, если учителя будут использовать на уроках задания на готовые чертежах: задачи на выделение объекта и записи его названия; задачи на комбинацию фигур; задачи на нестандартное расположение фигуры; задачи на доопределение условия; задачи на формулирование требования.