Аналитическая модель околоземной магнитопаузы по данным спутников «Прогноз» и «Интербол»

Первый спутник серии Прогноз был запущен в 1972 г ., с тех пор было запущено 12 космических аппаратов , включая « Интербол -1» и « Интербол -2» (« Прогноз -11» и -12 соответственно ). Для исследо вания влияния солнечного ветра на околоземное пространство эти спутники выводились на сильн о вытянутую эллиптическую орбиту , позволявшую пересекать различные плазменные области в около земном пространстве и исследовать их границы . В первых работах по данным спутников « Прогноз » и « Прогноз -2» [1-4] было установлено , что средние положения околоземных ударной волны и магнито паузы вполне соответствуют предсказаниям газоди намической модели [5]. В дальнейшем более де тальный статистический анализ положения и формы околоземной ударной волны , выполненный по дан ным спутников « Прогноз », « Прогноз -2», -4, -5, -7, -12 и данным других спутников [6] показал недоста точность газодинамического подхода для детально го описания этой границы . Вначале по данным спутника « Магион -4» ( субспутник « Интерб ола -1») [7] и затем по данным спутников серии « Прогноз » [8] была обнаружена зависимость положения удар ной волны от альфвеновского числа Маха и направ ления межпланетного магнитного поля и выявлена асимметрия ударной волны . Для анализа поведения ударной волны в зависимости от параметров сол нечного ветра и межпланетного магнитного поля ( ММП ) Веригиным и др . [9, 10, 7] была разработана полуэмпирическая модель ударной волны . При ее построении использовалась осесимметричная мо дель препятствия в потоке солнечного ветра около земной магнитопаузы Шу и др . [11], зависящая от двух переменных - динамического давления сол нечного ветра р V 2 и B z - компоненты ММП .

Имеется много других аналитических моделей магнитопаузы, используемых для эмпирического описания этой границы. Это, например, модели [12-18]. Подсолнечная часть всех этих осесимметричных моделей может быть аппроксимирована коническим сечением y2(x) = 2R0 (r - x) + bо(r - x)2, где ось x направлена против скорости солнечного ветра, y – расстояние от оси x. Параметры r0, R0, b0 для различных моделей приведены в табл. A1 работы [19]. Однако такая аппроксимация магнитопаузы не представляется реалистичной для описания положения геомагнитного хвоста, поскольку эллипсоиды (b0<0 ) достаточно быстро схлопываются за планетой, а параболоиды (b0 = 0) и гиперболоиды (b0>0) приводят к его бесконечной асимптотической толщине.

В настоящей работе динамика околоземной маг нитопаузы рассмотрена по данным спутников серии « Прогноз » и предложено аналитическое выражение для описания ее положения и формы от подсолнеч ной точки до дальнего геомагнитного хвоста в зави симости от параметров набегающего потока солнеч ного ветра . В отличие от предшествующих исследо ваний для анализа зависимости параметров нашей модели от B _z- компоненты ММП используется мно гомерная нелинейная оптимизация , а не поиск такой зависимости в результатах простой аппрок симации методами фильтрации / сглаживания , что в случае нелинейных процессов может привести к не вполне адекватным результатам .

Описание экспериментальных данных

Все спутники серии «Прогноз», кроме «Прогноза-9» и «Интербола-2», имели похожие эллиптические орбиты с апогеем ~31RE (RE – радиус Земли), перигеем ~0.1 RE, наклонением ~65° и периодом ~4 сут. Орбита «Прогноза-9» была гораздо более вытянутая с апогеем ~110RE и периодом около 26 сут. Данные «Интербола-2», который имел ~6-часовую полярную орбиту и выходил в солнечный ветер только в области каспа, здесь не используются. Энергетические спектры ионов измерялись с помощью широкоугольных плазменных анализаторов [20-22]. Пересечения магнитопаузы определялись по характерным изменениям параметров плазмы и энергетических спектров ионов. При входе спутника в магнитосферу из магнитослоя и пересечении магнитопаузы существенно возрастает величина магнитного поля, резко меняется его направление, ионы с энергиями солнечного ветра (50 эВ – 5 кэВ) или перестают наблюдаться, или их плотность сильно падает.

Для анализа был создан массив данных, включающий 331 пересечение магнитопаузы спутниками «Прогноз», «Прогноз-2», 4–6, 9 в период с 1972 по 1983 г., а также 2625 пересечений магнитопаузы спутником «Интербол-1» в 1995 и 1999 г. (рис. 1). Массив данных по пересечениям магнитопаузы был специально создан по имеющимся первичным экспериментальным данным. Использовались среднечасовые параметры солнечного ветра и ММП, представленные на сайте , относящиеся к часу пересечения или к предыдущему часу, если пересечение было зарегистрировано в первые 15 минут часа.

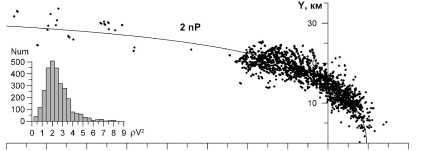
-80       -70       -60       -50      -40       -30       -20      -10       0        10       20 X, КМ

Рис . 1. Наблюдавшиеся положения пересечений магни топаузы ( точки ) и ее рассчитанное положение ( тонкая кри вая ) при динамическом давлении солнечного ветра 2 нПа . На врезке показана гистограмма распределения всех на блюдавшихся пересечений магнитопаузы по ρ V² .

Анализ данных

Созданный массив экспериментальных данных по положению магнитопаузы около Земли использовал ся в этой работе для построения модели магнитопау зы и затем для анализа ее вариаций в зависимости от параметров набегающего потока солнечного ветра .

В литературе используются различные выражения и подходы для описания магнитопаузы - как чисто эмпирические , так и основанные на рассмотрении баланса давлений [5, 12, 15, 18 и др .]. Здесь мы бу дем использовать выражение

На рис . 1 приведены все имеющиеся пересечения магнитопаузы спутниками серии « Прогноз ». Как вид но на врезке , пересечения магнитопаузы наиболее час то происходили при динамическом давлении солнеч ного ветра ρ V² = 2 нПа . Тонкой линией показано по ложение магнитопаузы , рассчитанное по формуле (1) с учетом выражений (2) при таком динамическом дав лении . Видно разумное соответствие модельной кри вой экспериментальным данным .

На рис . 2 показаны пересечения магнитопаузы при различных динамических давлениях солнечного ветра . Приведены интервалы давлений , для которых были отобраны пересечения магнитопаузы и средние

y ( x ) =    arctan

π

( П _ „----- г)

I D 2 RR о( ^г о - x ) I или

x ( y ) = r ₀

D ² 2 π ² R ₀

tan2

Y, км

где r ₀ – расстояние от центра Земли до подсолнеч ной точки магнитопаузы , R ₀ – радиус кривизны маг нитопаузы в подсолнечной области , D – диаметр магнитного хвоста при большом удалении от Земли ( x → - ∞ ).

Вначале предположим , что параметры r ₀, R ₀, D зависят только от динамического давления набегаю щего потока солнечного ветра ρ V² , причем обратно пропорционально корню шестой степени из ρ V² . Тогда по имеющемуся массиву данных , минимизи руя среднеквадратичное отклонение наблюдавших ся положений магнитопаузы от поверхности (1), можно получить :

r 0 = 10.8 R E ( ρ V² )^-1/6,

R 0 = 16.9 R E ( ρ V² ) )^-1/6, (2)

D = 94.5 R E ( ρ V² ) )^-1/6.

При этом среднеквадратичное отклонение экспе риментальных точек от поверхности (1) c парамет рами (2) составляет ^ ( о ² ) =1.358 R Е .

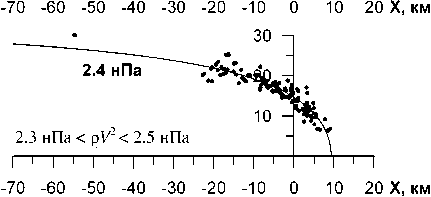
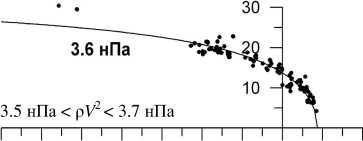
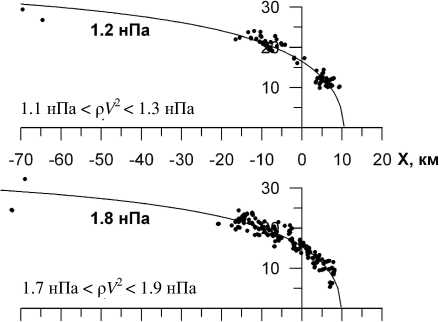
-70 -60 -50 -40 -30 -20 -10 0   10 20 X, км

Рис . 2. Наблюдавшиеся положения магнитопаузы ( точки ) и ее рассчитанные положения ( тонкие линии ) для различных динамических давлений солнечного ветра .

давления , использовавшиеся при расчете соответст вующих модельных зависимостей . Рисунок 2 свиде тельствует о хорошем соответствии модели имею щимся экспериментальным данным .

Для исследования , возможно , различной зависи мости параметров r ₀, R ₀, D от динамического давле ния солнечного ветра и их возможной зависимости от В _z- компоненты ММП в солнечно - магнитосфер ной системе координат рассматривались более сложные выражения для этих параметров :

r 0 = af ( B z )( ρ V² )^{- d}R 0 = bf ( B z )( ρ V² )^{- e}D = cf ( B z )( ρ V² ) ^f . (3)

Для функции f ( В z ) предполагались два обычно ис пользуемых выражения f ₁( B _z) =1 + g tanh( h ( B _z- B _zo)) и f 2 ( B z ) = 1 + g ( B z - B zo ) при B z <  B zo , f 2 ( B z ) = 1 + h ( B z – B zo ) при B _z> B _zo. По имеющимся экспериментальным данным подбиралось не более шести параметров одновременно при различных условиях на осталь ные . Результаты расчетов приведены в таблице .

Оказалось , что вариации показателя степени в зависимости от ρ V² практически не изменяют средне квадратичное отклонение экспериментальных точек от модельной кривой , поэтому далее при анализе зависимости от вертикальной компоненты магнит ного поля мы полагали d = e = f = –1/6.

На рис . 3 показан разброс в зависимости от В z нормированного подсолнечного расстояния , полу ченного проецированием измеренных точек пересе чения в подсолнечную область вдоль модельной маг нитопаузы (1) и приведением полученных значений к ρ V² =1. Показаны также рассчитанные зависимо сти подсолнечного расстояния от В _z, соответствую щие двум последним строкам в таблице . Из рис . 3 видно , что по данным спутников серии « Прогноз » подсолнечное расстояние от центра Земли до магни топаузы практически не зависит от В _z- компоненты ММП . Об этом же свидетельствует незначительное уменьшение 〈 σ ² 〉 при проведении шестипарамет рической оптимизации по сравнению с более про стой оптимизацией по трем параметрам ( первая строчка в таблице ). Таким образом , далее для расче та положения и формы магнитопаузы будет исполь зоваться выражение (1) с параметрами , рассчиты ваемыми по формулам (2).

Ранее на существование зависимости положения магнитопаузы от В _z указывали , например , Петринец [23] и Сайбек и др . [24]. В этих работах анализирова -

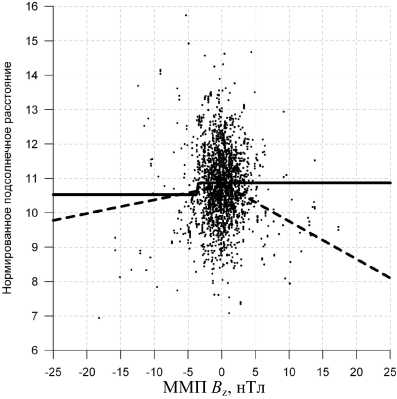
Рис . 3 . Нормированное по давлению солнечного ветра подсолнечное расстояние как функция В _z по данным спутников серии « Прогноз ». Сплошная линия соответству ет зависимости r ₀ = 10.7+1.71th(33.5.( B _z+3.6)), а штриховая ломаная – зависимости r ₀ = 11+ 0.04 ^. ( B _z–0.5), B _z< 0.5, r ₀ = = 11–0.1( B z –0.5), B z > 0.5.

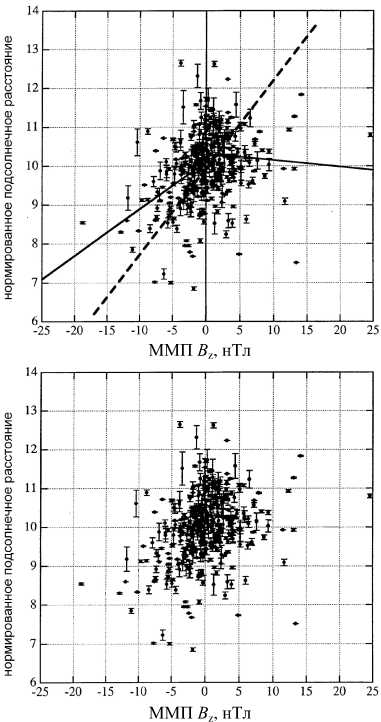
Рис . 4. Нормированное подсолнечное расстояние в зависимости от B _z по данным спутников ISEE-1, 2. Вверху штриховой линией проведена зависимость r ₀= = (11.3 + 0.25 B _z)2.04 ^-1/6 [24]; сплошной ломаной показа на зависимость r ₀ = 10.1 + 0.12 B _z при B _z<0 и r ₀ = 10.3–0.02 B _z при B z <0 [23].

Оптимизи руемые па раметры	Постоян ные па раметры	Условия	〈 σ 2 〉	Примечания
a , b , c	d = e = f = = -1/6	g = h =0	1.358
a , b , c , d		g = h =0; e = f = d	1.357
a , b , c , d , f		g = h =0; e = d	1.355
a , b , c , d , e		g = h =0; f = d	1.356
a , b , c , d , e , f		g = h =0	1.353	Нереалистич ные d , e , f
a , b , c , g , h , B zo	d = e = f = = -1/6	f ( B z )= f 1	1.354
a , b , c , g , h , B zo	d = e = f = = -1/6	f ( B z )= f 2	1.343

0.8 нПа <  ρ V ² < 1.2 нПа      1.8 нПа <  ρ V ² < 2.2 нПа 3.7 нПа <  ρ V ² < 4.3 нПа      2.8 нПа <  ρ V ² < 3.2 нПа

90                                          90                                          90                                          90

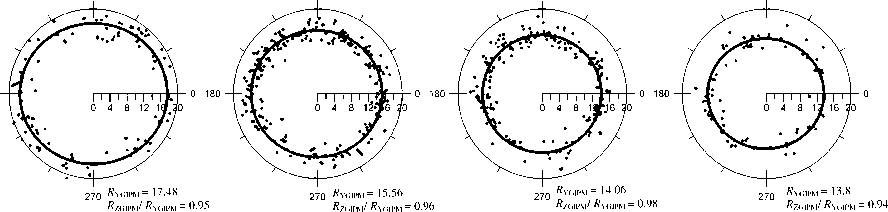
Рис . 5. Проекции точек пересечения магнитопаузы на плоскость терминатора для различных динамических давлений невозмущенного солнечного ветра . Показаны овалы , аппроксимирующие сечение магнитопаузы плоскостью терминатора .

Для каждого сечения указан его радиус вдоль оси Y_gipm и отношение радиусов вдоль осей Z_gipm и Y_gipm.

лись данные спутников ISEE-1, 2. Однако получен ные в этих работах зависимости , показанные на рис . 4 вверху , выглядят неубедительно : если убрать прове денные зависимости ( рис . 4, внизу ), поле точек ско рее свидетельствует о большом разбросе подсолнеч ных расстояний независимо от В _z, как и на рис . 3.

Полученные эмпирические выражения (1), (2) для описания околоземной магнитопаузы позволили выявить не известную ранее особенность этой гра ницы . На рис . 5 точки пересечения магнитопаузы спроектированы вдоль модельной поверхности на плоскость терминатора . Здесь используется геоцен трическая система координат GIPM (Geocentric Interplanetary Medium), в которой ось X gipm направлена против скорости невозмущенного солнечного ветра , а вектор ММП лежит во втором или четвертом квад ранте плоскости (X gipm , Y gipm ) [6]. Пересечения магни топаузы разделены по величине наблюдавшегося давления невозмущенного солнечного ветра . Кроме ожидаемого сжатия всей магнитопаузы при повы шении давления , видно , что магнитопауза сжата приблизительно на 5 % сильнее в направлении , пер пендикулярном плоскости , содержащей векторы ско рости солнечного ветра и ММП . Это сжатие , возмож но , является результатом натяжения силовых линий магнитного поля в магнитослое при обтекании магни тосферы Земли солнечным ветром с вмороженным в него ММП , обволакивающим магнитопаузу .

Заключение

По данным спутников «Прогноз», «Прогноз-2», 4–6, -9 и «Интербол-1» для описания положения и формы околоземной магнитопаузы предложена удобная аналитическая формула, при этом при x→ -∞ магнитопауза имеет конечный асимптотический диаметр, что согласуется с дальними пересечениями хвоста магнитосферы спутником «Прогноз-92. Эмпирическая аналитическая модель магнитопаузы учитывает только зависимость формы и положения магнитопаузы от динамического давления набегающего потока солнечного ветра. По данным спутников серии «Прогноз» не удалось обнаружить зависимость магнитопаузы от Вz-компоненты ММП . При этом надо иметь в виду, что рассматривались часовые средние значения параметров солнечного ветра, и поэтому речь не может идти о быстрых откликах магнитопаузы на изменения в солнечном ветре .

Данные спутников серии « Прогноз » свидетель ствуют о том , что магнитосфера Земли сжата при близительно на 5 % в направлении , перпендикуляр ном плоскости , содержащей векторы скорости сол нечного ветра и ММП . Это сжатие , вероятно , явля ется результатом натяжения силовых линий ММП в магнитослое при обтекании магнитосферы Земли солнечным ветром .

Полученную эмпирическую модель магнитопау зы удобно использовать для моделирования и ана лиза вариаций положения и формы околоземной ударной волны . Модель легко может быть включена в полуэмпирическую модель ударной волны Вери гина и др . [7, 9, 10]

Работа выполнена при частичной поддержке программ РАН П 16.2 и ОФН 16 и гранта РФФИ № 07-02-92210- НЦНИЛ _ а .