Аналитическая модель плотности верхней атмосферы Земли для баллистико-навигационного обеспечения полётов космических аппаратов

Сухой Ю.Г.

БраГинец в.ф.

МоШнин а.а.

Применение моделей плотности атмосферы при навигационно-баллистическом обеспечении полётов космических аппаратов

При навигационно-баллистическом обеспечении (НБО) полётов низкоорбитальных космических аппаратов (КА)

наибольший вклад в ошибки моделирования элементов орбиты вносит неточность учёта возмущающих сил, обусловленных влиянием плотности атмосферы. Для описания используемых при НБО моделей плотности атмосферы применяют методы моделирования на основе обработки приборных измерений параметров атмосферы или данных об ошибках моделирования (прогнозирования) параметров движения КА. При этом модели могут иметь аналитический вид или строиться на основе таблиц. Полученные с помощью указанных методов модели делятся на статические и динамические. Наиболее широко применяются динамические модели [1–7], так как они учитывают влияние на состояние плотности атмосферы гелио-геофизических условий. Недостатком большинства динамических моделей плотности атмосферы [1–4], используемых при определении орбит и прогнозировании движения низкоорбитальных КА, является отсутствие простых, быстродействующих и достаточно точных аналитических зависимостей, позволяющих надёжно рассчитывать частные производные от измеряемых параметров по уточняемым параметрам, в т. ч. и по параметрам модели верхней атмосферы Земли. Одной из таких моделей является «Модель плотности верхней атмосферы Земли в диапазоне высот от 120 до 600 км» (S-89) [5], построенная на основе анализа результатов торможения спутников на высотах 180…660 км при различных уровнях солнечной и геомагнитной активности. В модели нет таблично заданных функций, что позволяет при определении параметров движения КА более корректно использовать производные от измеренных навигационных параметров по варьируемым параметрам атмосферы. Дальнейшим развитием модели S-89 является модель SBM-2022 [6], в которой скорректированы формулы модели S-89, исходя из полученных в последнее время экспериментальных данных о торможении низкоорбитальных КА. В работе [7] приведено обновление модели SBM-2022, обеспечивающее расчёт значений плотности атмосферы для высот 600…1 500 км на основе дополнительных экспериментальных данных и данных моделей [1–4]. Настоящая статья даёт полное описание модели SBM-2022. В ней также проведено сравнение SBM-2022 с отечественной моделью ГОСТ Р 25645.166-2004 [1] и современными зарубежными моделями NRLMSISE-00 [2], NRLMSIS 2.0 [3], как наиболее точными моделями, используемыми при НБО полётов КА. Модель SBM-2022 является аналитической, построенной главным образом на основе статистических данных о торможении КА, что может давать определённое преимущество при её применении для прогнозирования движения КА в атмосфере Земли. Модели [2, 3] построены на основе непосредственного измерения температуры и состава атмосферы и являются сложными для использования в НБО, а модель [1] содержит большое количество таблично заданных функций, что также вызывает трудности при её использовании. Параметры предлагаемой модели могут уточняться различными математическими методами, например, методом наименьших квадратов, в т. ч. при существенных отклонениях моделируемой плотности атмосферы от фактической за счёт климатологических особенностей термосферы, возникающих под влиянием аномальных гелиогео-физических факторов [8, 9].

основное соотношение аналитической модели плотности атмосферы земли

Общая формула модели имеет вид, представленный в работах [5–7]. В качестве входных данных модели используются местоположение КА, день года, время суток, солнечная активность и геомагнитная возмущённость. В общем виде модель представлена формулой

ρ = ρ K– K~K + Δρ + Δρ + Δρ , (1) ср F81 F kp с г п, в которой ρср — средняя статическая часть модели плотности атмосферы; KF– , KF~, Kkp — коэффициенты влияния ср8е1днего уровня солнечной активности, среднесуточных вариаций солнечной активности и геомагнитной возмущён-ности соответственно; Δρс — суточная вариация плотности; Δρг — годовая вариация плотности; Δρп — полугодовая вариация плотности.

Средняя статическая часть модели плотности атмосферы

В формуле (1) средняя статическая часть модели описывается как функция плотности от высоты без учёта возмущающих факторов, суточных, годовых и полугодовых вариаций. До высоты 120 км принимается, что плотность атмосферы мало зависит от гелиогеофизических условий и определяется как ρ = ρср, а ρср вычисляется по ГОСТ 4401-81 [10]. До высоты 600 км средняя статическая часть плотности в зависимости от высоты Н описывается аналогично модели [6]:

ρ ср

= A ср

_Н   n ср

Н

где

n _cp = n ₀ + K ₀

H ₀ – H ^{n 01}

α′

при H ≤ 290 км;

n _cp = n ₀ + K ₀

H – H ₀ α′

ⁿ 01

H – H ₀ ^{n 02}

α″

при H > 290 км.

Коэффициенты формул (2)–(4) имеют следующие значения: A _ср = 2,519∙ 10^–10 кг∙м^–3; H _ср = 200,0 км; n ₀ = 6,34; K ₀ = 0,26; H ₀ = 290,0 км; α′ = 100,0 км; α″ = 141,13 км; n ₀₁ = 4,25; n ₀₂ = 4,37.

Для высот 600…1 500 км используется формула (2) с другими параметрами, в ней

Н2 Н ncp = K01 α′ + K02 α′ + K03;

A _ср = 1,0852∙10^–13 кг∙м^–3;

H _ср = 600,0 км;

K ₀₁ = 0,0593; K ₀₂ = –1,7433; K ₀₃ = 18,8650.

зависимость плотности атмосферыот среднего уровня солнечной активности

Зависимость плотности атмосферы от среднего уровня солнечной активности учитывается с помощью потока радиоизлучения Солнца в дециметровом диапазоне F _10,7. В качестве средней величины F _10,7 принято его средневзвешенное значение за 81 день. Для этого применено следующее распределение по номеру дня:

P i = P 1 + 2

¹ - P 1

( N + 1) N

i ,

где i — порядковый номер дня; N = 81; P ₁ = 0,0233.

Формула для опр_–еделения средневзвешенного значения F имеет вид

N

FP ii

F 81 = ⁱ N ¹     ,

Σ Pi i = 1

где F_i — осреднённое за сутки значение индекса F _10,7.

Для получения расчётных формул экспериментальные данные о плотности были разбиты на две группы: к первой отнесены данные, полученные в периоды F^– ₈₁< 110∙ 10^–22 Вт/(м² ∙ Гц), ко второй — в периоды F^– ₈₁ ≥ 110∙ 10^–22 Вт/(м² ∙ Гц).

Спокойная гелиогеофизическая обстановка характеризовалась индексом геом _– агнитной активности А_p = 12 и F ₈₁ ≈ 110∙ 10^–22 Вт/(м² ∙ Гц). Изменения плотности относительно средней плотности ρ _ср определялись в виде соотношения

ρ F – /ρ ср = f ( H , F^– 81 ).

Путём выравнивания данных по математическим ожиданиям выборочных совокупностей первой группы для высот 120…600 км получено выражение

ρ _F – /ρ_ср = (1 – β′lg( g )/2) g ′.

Для второй группы подтверждено выражение модели S -89 [5]:

ρF– /ρср = 1 + β″ (H/α)2, где α = 100 км.

Множитель β′ представлен в виде степенной функции

β′ = a ₁′ + a ₂′

F ^– + a ′₃ ^{n ′} a ₄′

множитель β″ также представлен в виде степенной функции с дополнительным слагаемым

β″ = a ₁″

+ a ₂″

F ^– + a ″ ⁿ _{a 4 ″} 3

+

F ^– + a ₅ a ₆

Выражение функции g найдено в виде:

g _{= ( H /}α₎ H / α –( H / α ) ² /10 _.

Коэффициенты a ₁ и a ₃ были определены методом наименьших квадратов применительно к обеим группам данных о плотности при различных значениях n . Затем были выбраны коэффициенты, при которых среднеквадратическое отклонение расчётных значений ρ от моделируемых было наименьшим. В результате были получены следующие наборы коэффициентов для высот 120…600 км: для первой группы данных a ′₁ = 1,083; a ′₂ = –1,000; a ′₃ = –7∙10^–22 Вт/(м²∙Гц);

a ′₄ = 100,0∙ 10^–22 Вт/(м²∙Гц);

n ′ = 3,00; g ′ = 1,06;

для второй группы a ₁″ = –0,0125; a ″₂ = 0,1000; a ″₃ = –85,0∙ 10^–22 Вт/(м²∙Гц);

a ″₄ = 100,0 ∙10^–22 Вт/(м²∙Гц); n ″ = 1,50;

a ₅ = –110,0∙10^–22 Вт/(м² ∙Гц);

a ₆ = 3 415,0∙10^–22 Вт/(м² ∙Гц).

Для диапазона _– высот 600…1 500 км для первой группы [ F ₈₁< 110∙ 10^–22 Вт/(м² ∙ Гц)] получено следующее выражение:

ρF– /ρср = AF–′(F–10,7/α′)n′, 81         , где

A – = a ′( H /α′)³ + a ′( H /α′)² + a ′( H /α′) + a ′.

Для высот вы–ше 600 км для второй группы [F81 ≥ 110∙ 10–22 Вт/(м2 ∙ Гц)] получены разные формулы для двух диапазонов высот:    600 < H ≤ 860 км и 860 < H ≤ 1 500 км.

Для диапазона 600 <  H ≤ 860 км изменение плотности под действием среднего уровня солнечной активности имеет вид

ρF– /ρср = AF– ″ (F10,7/α′)n, 81          , где AF–8″1 = a″1 (H/α′)2 + a2″ (H/α′) + a″3.

Для диапазона 860 <  H ≤ 1 500 км формула отличается множителем у степенной функции и показателем степени

ρF– /ρср = AF– ″′(F10,7/α′)n , 81          , где

A – = a ″′( H /α′)³ + a ″′( H /α′)² + a ″′( H /α′) + a ″′. 81

В результате обработки экспериментальных данных для первой группы были получены следующие коэффициенты:

a ′₁ = 9,0128∙10^–4; a ₂′ = –3,3831∙10^–2;

a ′₃ = 4,7219∙10^–1; a ′₄ = –1,1855; n ′ = 3,07.

Для второй группы коэффициенты имеют значения: a ″₁ = –3,8305 ∙ 10^–2;

a ″₂ = 5,5321∙10^–1; a ″₃ = –1,1481; n ″ = 3,01;

a ₁″′ = –6,4423∙10^–4; a ″₂ ′ = 2,6545∙10^–2; a ″₃ ′= –0,3651; a ″₄ ′= 2,4283; n ′″ = 2,66; α′ = 100,0 км.

зависимость плотности от среднесуточных вариаций солнечной активности

В то время как значения F _10,7, осреднённые за период несколько месяцев, характеризуют изменение среднего уровня солнечной активнос _~ ти в её 11-летнем цикле, значения F _10,7, осред-нённые за один или несколько дней, характеризуют интенсивность радиоизлучения активных областей на Солнце, т. е. случайную составляющую солнечной активности относительно её среднего уровн _~ я. Зависимость ρ _F ~ /ρ _F – при изменении F определена, аналогично работам [5–7], в виде выражения

ρρF~F– = 1 + γ (F~ – F–81)/F–81, где γ = f (H, F–81).

Коэффициент γ на основе обработки экспериментальных данных определён для диапазонов высот 120 ≤ H ≤ 900 км и 900 <  H ≤ 1 500 км. До высоты 900 км включительно γ описывается уравнением

γ = [ b ₁ + b ₂( F^– ₈₁/ b ₃)]( H /α′)³ +

+ b ₄( H /α′)² + b ₅( H /α′) + b ₆.             (5)

Коэффициенты формулы (5) имеют значения: b ₁ = –0,01148; b ₂ = 0,00095; b ₃ = 100,0∙10^–22 Вт/(м²∙Гц); b ₄ = 0,1105; b₅ = –0,0739; b ₆ = –0,0803; α′ = 100,0 км.

Для высоты H > 900 км уравнение упрощается до вида

γ = b 7 F81, где b7 = 0,0006.

зависимость плотности атмосферы от уровня геомагнитной возмущённости

Зависимость плотности атмосферы от уровня геомагнитной возмущённости находилась с использованием трёхчасового индекса геомагнитной возмущённости Kp. Время задержки изменения плотности τkp относительно изменения Kp принималось равным 6 ч (τkp = 6 ч). Для высот 120 ≤ H ≤ 1 500 км получены следующие соотношения ρkp /ρF– с разбиением на три диапазона:

• 1)    для 120 ≤ H ≤ 600 км

ρkp /ρF– = 1 + Akp [c0(H/α″) + c1];(6)

• 2)    для 600 <  H ≤ 1 080 км

ρ kp /ρ F – = 1 – A kp [ c 0 ( H /α″) + c 2 ] +

+ (c3Kp + c4)(H/α′ + c5);(7)

• 3)    для H > 1 080 км

ρ /ρ = 1 + c K + c ,(8)

kp F             6 p7

где

A kp = c 8 { [ c 9 ( F 81 / c 18 )² + c 10 ( F 81 / c 18 ) + c 11 ] K p ³ +

+ [ c 12 ( F^– 81 / c 18 )² + c 13 ( F^– 81 / c 18 ) + c 14 ] K p ² +

+ [c15(F–81/c18) + c16] Kp + c17}.(9)

Коэффициенты в формулах (6)–(9) имеют следующие значения: c ₀ = 2,0833; c ₁ = –0,25; c ₂ = –2,25; c ₃ = 0,00677;

c ₄ = –0,0152; c ₅ = –6,0; c ₆ = 0,0325;

c ₇ = –0,0730; c ₈ = 1,0035; c ₉ = 0,004770; c ₁₀ = –0,018246; c ₁₁ = 0,025104; c ₁₂ = –0,03546; c ₁₃ = 0,13292; c ₁₄ = –0,18791; c ₁₅ = –0,0719; c ₁₆ = 0,3877; c ₁₇ = –0,37;

c ₁₈ = 100,0·10^–22 Вт/(м²∙Гц); α″ = 1 000,0 км.

расчёт относительной амплитуды суточной вариации плотности

Суточные вариации плотности атмосферы, зависящие от уровня солнечной и геомагнитной активности, широты и высоты полёта КА над поверхностью Земли, представлены как результат вздутия атмосферы в дневное время.

Для относительной амплитуды суточных вариаций плотности атмосферы A ( A = ρ_{c макс}/ρ_{c мин}) получены следующие выражения для различных диапазонов высот:

• •    для 120 ≤ H ≤ 600 км

  A = γ₁( F ) + γ₂( F )

  
  

  Н

  
  

  d 1

  
  

  d 0

  
  

• •    для 600 <  H ≤ 1 200 км

  
  

Н ^d

A = γ₁( F ) + γ₂( F ) d ₂ – _{d 0} + d ₃

;

• •    для 1 200 <  H ≤ 1 500 км

A = γ1(F), где d0 = 100,0 км; d1 = 0,8; d2 = 4,2; d3 = –6,0.

Выражение γ₁( F ) имеет вид

γ₁( F ) = d ₄ + d ₅

|F 81 + d 6 | ^{n γ 1} d 7

Коэффициенты формулы (10) имеют следующие значения: d ₄ = 0,9702; d ₅ = –0,7289; d ₆ = –60,0∙10^–22 Вт/(м²∙Гц);

d ₇ = 1 000,0 ∙10^–22 Вт/(м² ∙Гц); n _{γ 1} = 0,45.

Выражение для функции   γ₂( F )

имеет вид

γ₂( F ) = d ₈ + d ₉

|F ₈₁ + d ₆| ^{n γ 2}

d 7

где d ₈ = 1,000; d ₉ = –1,000; n _{γ 2} = 0,70.

расчёт смещения экстремумов суточной вариации плотности, широтного изменения амплитуды и преобразование относительного значения амплитуды суточной вариации в абсолютное

Зависимости времён экстремумов суточной вариации плотности от высоты для различных широт соответствуют работе [5], так как экспериментальных данных для их уточнения было недостаточно. Для описания широтного изменения амплитуды суточной вариации также использована формула [5–7, 11]

c o s ^m Ψ – sin ^m Θ

Rϕ = R 1 + RsinmΘ где R — амплитуда суточной вариации ρc макс

Δρ R =       ; Ψ = |ϕ – δ |/ m ; Θ = |ϕ + δ |/ m ;

c

ρ0

m = 2,50; m ₁ = 2,00; ρ_{c макс} — максимальное значение ρ в суточном распределении; ϕ — широта; δ₀ — склонение Солнца.

Амплитуда суточной вариации R определяется через относительную амплитуду A = p c макс / p c мин по формуле

R =

| A – 1| A + 1 ^.

Абсолютная амплитуда B ф суточной вариации Apc на заданной широте ф вычисляется по формуле

B ф = Р о R ф .

расчёт общей аналитической функции суточного изменения плотности

Распределение вариаций p на определённой широте в течение суток представлено в виде функции местного времени Ap c = B J ( t ) для дневного и ночного изменения плотности так же, как в работах [5–7]. Функция зависимости плотности от местного времени f ( t ) описана соотношением

f(t) = f1 + f2|t – tэкс|nf, где t — текущее местное время; tэкс — времена экстремумов (ночной минимум или дневной максимум); f1, f2 — коэффициенты. Используемые параметры имеют следующие значения: для дневного максимума f‘ = 1,00; f ‘ = -0,0400 ч-1; tэкс = tмакс; nf1 = 2,00 при ограничении |t – tмакс| ≤ 5 ч, для ночного минимума f 1 = -Т00; f = 0,0103 ч-1; tэкс। = tмин; nf2 = 2,35 при ограничении |t – tмин| ≤ 7 ч. Если значение |t – tэкс| превышает заданные ограничения, то tэкс фиксируется в пределах данного ограничения.

Общая аналитическая функция суточного изменения вариаций плотности атмосферы имеет вид

^AP c = Р о RJ ⁽ t ).

расчёт годовой и полугодовой вариаций плотности атмосферы

Формула для описания годовых и полугодовых вариаций соответствует работе [7], применяется для всех высот и имеет вид

Арг,п = Ро{ A rcos[Q( d - D г)] + A пCos[2Q( d - D п)]}, где Aг — нормированная амплитуда годовой вариации; Aп — нормированная амплитуда полугодовой вариации; d — номер дня в году; Dг — фаза годовой вариации; Dп — фаза полугодовой вариации; Q = 2п/365 — угловая частота движения Земли вокруг Солнца.

Функция для нормированной амплитуды годовой вариации определяется выражением

Aг = k1 + k2/H, где k1 = –0,005; k2 = 18,00 км.

Функция для нормированной амплитуды полугодовой вариации удовлетворяет соотношению

Aп = k3(k4 + k5H/k6), где k3 = 0,9; k4 = 0,075; k5 = 0,0250; k6 = 100,00 км.

Фазы вариаций имеют значения D _г = 10 сут; D _п = 117 сут.

Широтные изменения плотности атмосферы для годовой и полугодовой вариаций не были выделены на фоне сезонных и суточно-широтных колебаний плотности.

Сравнительные результаты расчёта плотности атмосферы по различным моделям

Сравнение результатов моделирования плотности проводилось для разработанной модели SBM -2022 и четырёх наиболее часто используемых моделей плотности атмосферы (ГОСТ Р 25645.166-2004 (ДМА-2004) [1], MSIS00 [2], MSIS 2.0 [3] и MET-07 [4]) по произвольно выбранным данным из числа допустимых входных данных перечисленных моделей в диапазоне высот 120…1 500 км. Указанные модели использованы для сравнения, так как они получили наиболее широкое применение для баллистических расчётов при полётах низкоорбитальных КА.

На рис. 1 представлен график отклонения плотности, рассчитанной по модели SBM -2022, от плотностей, рассчитанных по моделям MSIS00 , MSIS 2.0, ДМА-2004 и MET-07, в процентах, при спокойных гелиогеофизических условиях Ар = 12 ( _– индекс геомагнитной возмущённости), F ₈₁ = 110 ∙ 10^–22 Вт/(м² ∙ Гц) (индекс средней солнечной активности). Плотность рассчитывалась для средней геофизической широты ф = 45° для 8 ч утра зимнего дня года (14 января).

Для зимних условий (рис. 1) максимальные отклонения плотности по модели SBM -2022 от плотности сравниваемых моделей составляют 83% на высоте ~460 км, а также на высотах более 900 км, где отклонения составляют ~50%. При этом на интервале высот 250…700 км, где тормозящее действие атмосферы наиболее существенно зависит от гелиогеофизических условий, отклонения плотности по модели SBM -2022 от плотностей, рассчитанных по зарубежным моделям MSIS00 ( MSIS2.0 ) и MET-07, существенно меньше, чем у модели ДМА-2004, отклонение которой от тех же моделей достигает 110%. На высотах более 800 км модель SBM -2022 даёт более близкие к модели ДМА-2004 значения плотности.

На рис. 2 представлен график отклонения плотности, рассчитанной по модели SBM -2022, от плотностей, рассчитанных по моделям MSIS00 , MSIS 2.0, ДМА-2004 и MET-07, в процентах, для возмущённых _– гелиогеофизических условий Ар = 48 и F ₈₁ = 150· 10^–22 Вт/(м² · Гц). Плотность рассчитывалась для средней геофизической широты ф = 45° на 20 ч вечера осеннего дня года (22 сентября).

Для данных условий модель SBM -2022 наиболее близка к моделям ДМА-2004 и MET-07. По сравнению с моделью ДМА-2004 максимальное отклонение составляет 73% на высоте ~1 280 км, а для высот 200…800 км отклонение не превышает 20%. Отличие от модели MET-07 в среднем составляет не более 45%, только на высоте, близкой к 600 км, оно достигает 64%.

Следует отметить, что для низкоорбитальных КА ошибки моделирования параметров их движения зависят от массы и формы КА. Аэродинамические силы и моменты для заданной формы КА определяются скоростью и плотностью набегающего газового потока, угловой ориентацией, а также линейными и угловыми ускорениями движения КА. Моменты сил для низкоорбитальных КА сложной формы малы и компенсируются системами ориентации и стабилизации, так как в большинстве случаев выдерживается определённая ориентация КА. Для большинства КА сила лобового сопротивления является определяющей, а подъёмная и боковая силы достаточно малы. В этом случае ускорение от тормозящего действия атмосферы по оси x, совпадающей с направлением скорости КА, выражается формулой

— 1 _

^W ax = ^- 2 M^C-^FP VV ⁽¹¹⁾

где C_x — безразмерный аэродинамический коэффициент; m — масса КА; F — характерная площадь (площадь миделевого сечения); р — плотность атмосферы; V , V — модуль и вектор скорости КА.

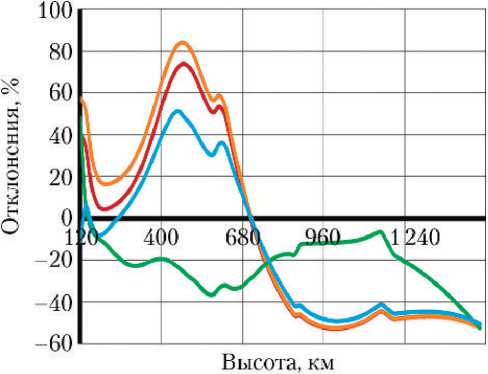
- MSIS00      - MSIS2.0

-ДМА-2004   -МЕТ-07

Рис. 1. Отклонение плотности в процентах по модели SBM-2022 от плотностей, рассчитанных по другим моделям, для зимнего дня года и спокойных гелиогео-физических условий

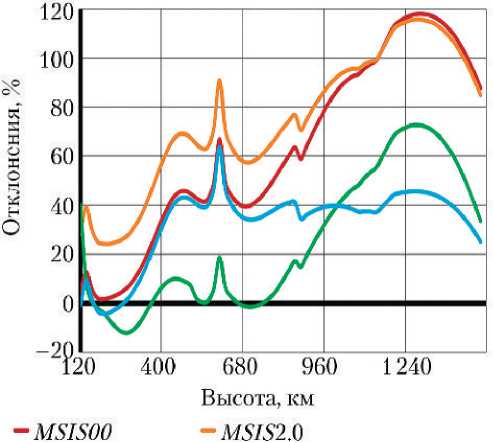
-ДМА-2004   -МЕТ-07

Рис. 2. Отклонение плотности в процентах по модели SBM-2022 от плотностей, рассчитанных по другим моделям, для осеннего дня года и возмущённых гелио-геофизических условий

Первые три члена в формуле (11) обозначаются как коэффициент S _δ , который принято называть баллистическим коэффициентом

S = ¹ C F . δ ₂ m x

Для КА с круговыми орбитами высотой ~200 км в зависимости от массы и формы КА отличие в моделировании плотности на 10% в спокойных гелиогеофизических условиях может приводить к ошибке прогнозирования движения КА вдоль орбиты на суточном интервале, равной нескольким десяткам километров, ввиду достаточно большой плотности атмосферы на этих высотах. На высотах 450–500 км, например, для КА «Ресурс-П», несоответствие в моделировании плотности на 50% приводит к ошибкам прогнозирования движения КА вдоль орбиты на суточном интервале ~400–500 м. Для КА типа «Ресурс-ДК» на высотах 550–600 км аналогичная ошибка может составить ~200–250 м.

Для компенсации этой ошибки в практике НБО баллистический коэффициент S _δ (12) используется в качестве коэффициента согласования S моделируемой и фактической плотности атмосферы Земли

S = S _δ ± Δ S . (13)

Таким образом, с учётом выражения (13) для моделируемого ускорения от сопротивления атмосферы применяется формула

^^^^^^^^^^^^™

—

WM = –SρMV V, где ρM — плотность, рассчитанная по используемой модели атмосферы.

На начальном этапе полёта для каждой модели атмосферы требуется подбирать своё значение согласующего коэффициента, однако, чем меньшей точностью обладает модель плотности, тем более затруднительно подбирать согласующий коэффициент. Практика показала, что при недостаточной точности модели плотности атмосферы согласующий коэффициент подвержен колебательным процессам, коррелирующим с реальными вариациями плотности атмосферы. Ввиду этого реальная точность моделей должна проверяться путём статистической обработки результатов прогнозирования движения КА на длительных интервалах времени с учётом значений согласующего коэффициента при различных уровнях солнечной активности и геомагнитной возмущённости, чему планируется посвятить дальнейшие статьи.

Таким образом, разработанная модель плотности верхней атмосферы SBM -2022 сопоставима с использующимися зарубежными моделями и моделью ДМА-2004, а в некоторых случаях, например, на высотах 250–700 км в спокойных гелио-геофизических условиях, она по значению плотности верхней части атмосферы занимает промежуточное положение между зарубежными моделями и отечественной ДМА-2004.

выводы

• 1.    Приведены соотношения для расчёта плотности верхней атмосферы Земли по разработанной авторами статьи модели SBM -2022 для высот 120…1 500 км.

• 2.    Проведён сравнительный анализ моделирования плотности верхней атмосферы Земли по разработанной модели SBM -2022 и по часто применяемым моделям плотности атмосферы ДМА-2004, MSIS 00, MSIS 2.0, MET-07 при спокойной и возмущённой гелио-геофизической обстановке. Сравнение показало, что разработанная модель плотности SBM -2022 сопоставима с использующимися зарубежными моделями и моделью ДМА-2004, а в некоторых случаях она по значению моделируемой плотности занимает промежуточное положение между зарубежными моделями и отечественной ДМА-2004.

• 3.    Модель SBM -2022 наряду с другими может быть рекомендована для практического использования при навигационно-баллистическом обеспечении низкоорбитальных КА и для проверки её

точности в сравнении с другими моделями путём статистической обработки результатов прогнозирования движения КА между соседними определениями орбиты по измеренным текущим навигационным параметрам на длительных интервалах времени при различных уровнях солнечной активности и геомагнитной возмущённости с учётом применяемого согласующего коэффициента.