Aniq integrallarning ba’zi tadbiqlari orqali matematika fanini kasbga yo’naltirib o’qitish ko’nikmasini shakllantirish

O‘zbekiston Respublikasi Prezidentining 07.05.2020 yildagi PQ-4708-sonli “Matematika sohasidagi ta’lim sifatini oshirish va ilmiy-tadqiqotlarni rivojlantirish chora tadbirlari to’g’risida”gi qarorining 1-ilovasidagi 3.1-bo’limining 14- “Matematika bakalavriat ta’lim yo‘nalishlari bitiruvchilarining muayyan aniq sohalarda amaliy masalalarni yechish ko‘nikmalarini rivojlantirish uchun ta’lim dasturlarini fanlar (yo‘nalishlar)aro integrativ prinsip asosida ixtisoslashtirilgan tartibda ishlab chiqish va joriy etish.” bandiga ko’ra bugungi kunga kelib, oliy ta’lim muassasalarida matematika fanini kasbga yo’naltirib o’qitish va hayotiy bog’liqlikda isbotlab o’qitish asosiy vazifalardan biri bo’lib qolmoqda [4]. Shularni inobatga olib ushbu maqolada asosan oliy ta’lim muassasalarining matematika darslari dasturiga kiritilgan aniq integrallar va ularning tadbiqlari mavzusini bir nechta misollardagi tadbiqlarini ko’rib o’tamiz. Aniq integrallar va ularning tadbiqlarini misollardagi tahlilini ko’rib chiqishdan oldin aniq integrallarning aylanma jism hajmini topishdagi bir nechta qo’llash mumkin bo’lgan formulalari bilan tanishib olamiz va misollardagi tadbiqlarini ko’rib chiqamiz.

Bizga [ a , b ] kesmada aniqlangan va uzluksiz bo’lgan y = f ( x ) funksiya berilgan bo’lib, V x e[ a,b ] uchun f ( x )>0 bo’lsin. Yuqoridan f ( x ) funksiya grafigi, yon tomonlardan x = a, x = b chiziqlar bilan, pastdan esa Ox o’qdagi [ a, b ] kesma bilan chegaralangan shaklni Ox o’q atrofida aylanishidan hosil bo’lgan T shaklning hajmi quyidagi (1) formula yordamida hisoblanadi [1]:

b

• V    = n j f ²( x ) dx        (1)

a

Bizga biror T jism berilgan bo’lib, uning Oy o’qqa parallel bo’lgan kesimlarining yuzasi ma’lum bo’lsin. Bu yuza x o’zgaruvchining funksiyasi bo’ladi, uni S = S ( x ) orqali belgilaymiz.

Agar S = S ( x ) funksiya [ a , b ] kesmada uzluksiz bo’lsa, T shaklning V hajmi quyidagi (2) formula yordamida topiladi [3]: b

• V    = j S ( x) dx        (2)

a

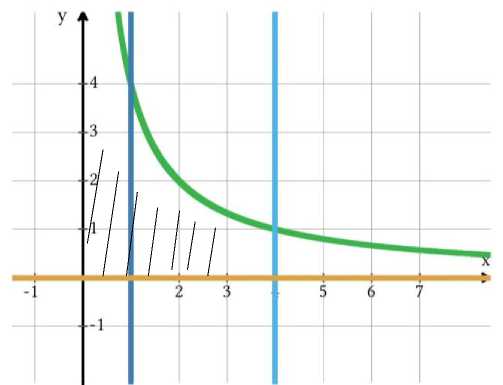
1-misol. Quyidagi xy = 4, x = 1, x = 4, y = 0 chiziqlar bilan chegaralangan shaklni Ox o’q atrofida aylantirishdan hosil bo’lgan aylanma jismning hajmini toping [2].

Yechilishi. D soha yuqoridan xy = 4 funksiya bilan, yon tomonlardan x = 1, x = 4 chiziqlar bilan, pastdan esa Ox ( y = 0) o’q bilan chegaralangan (1-rasm).

1-rasm

Endi D egri chiziqli sohani Ox ( y = 0) o’q atrofida aylantirishdan hosil bo’lgan aylanma jismning hajmini formula yordamida hisoblaymiz:

b

V = п j y ² dx =

a

16^    ^16

п I —ax = - п (— ) = xx

- п (4 -16) = 12 п

Javob: 12 п

П

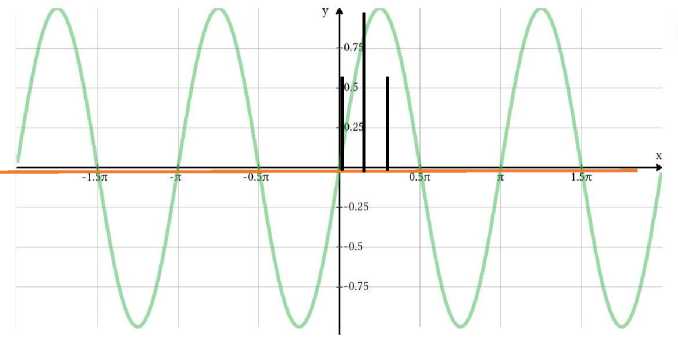
2-miSol. Quyidagi y = sin 2x,0 < x < —, y = 0 chiziqlar bilan chegaralangan shaklni Ox o’q atrofida aylantirishdan hosil bo’lgan aylanma jismning hajmini toping [2,3].

Yechilishi. D soha yuqoridan y = sin 2x funksiya bilan, pastdan esa Ox z             ,   1 '1       1           1                    Гл П 1 Z/^          \

( y = 0) o q bilan chegaralangan, x e [ 0;^ ] (2-rasm).

2-rasm

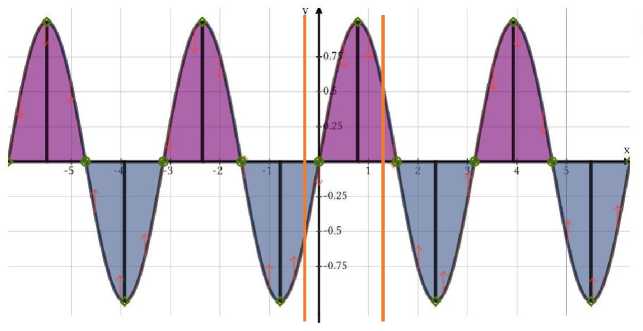
3-rasm

3-rasmda belgilangan D sohani Ox (y = 0) o’q atrofida aylantirishdan hosil bo’lgan aylanma jismning hajmini formula yordamida hisoblaymiz:

b

V = n j y ² dx =

П

П

n j sin² 2 xdx = n j (

a

П

1 - cos4 x          1    1              n²

-------) dx = n ((— x — sin 4 x ) ) = — 2      28      4

n2

Javob:

3-misol. Ushbu

2 x

- + У-a ² b ²

—

z

— = 1, z = ± c sirt bilan chegaralangan shakl c ²

hajmini toping [1,2].

Yechilishi. Dastlab berilgan tenglama bo’yicha bir pallali giperboloidni yasaymiz (4-rasm).

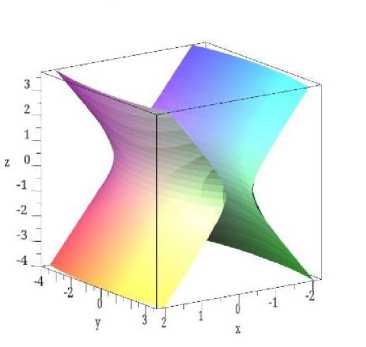
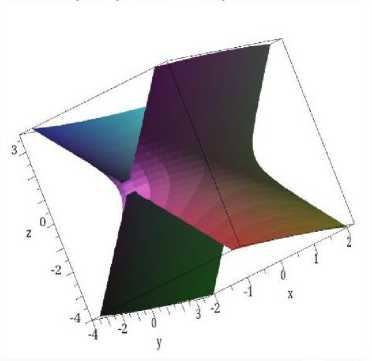
4-rasm

Giperboloidni Oxy tekislikka parallel bo’lgan, ze[-c;c] kesmada o’zgaruvchi, z=p tekisliklar bilan kesamiz. Kesimda ellips hosil bo’ladi (5-rasm)

222  22  2  22

^x , y _ p       ^x_ , y_      p    ^x yy_

2 +    2      2       ’       2 +    2           2 ’        2    ,2

abc  ab  c ab

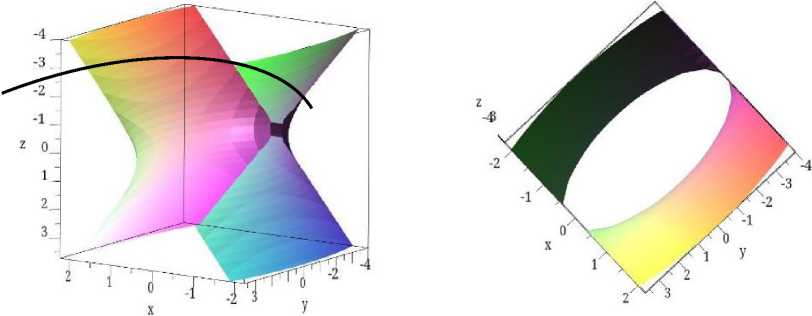
5-rasm

Bunda ellipsning yarim o’qlari:

a I 2 .    2              r b / 2 .    2

ax =- Cc + p        bj =- yc + p cc

Bu kesimning yuzlari p ga bog’liq bo’lgan ellips bilan chegaralangan yuzaga teng bo’ladi [5].

S ⁽ p ) = rnp b = ^ab ( c ² + p ²) c

Kesim yuzidan foydalanib, berilgan jism hajmini topamiz:

f           c nab, ₇       ,    2nab, ₇ p³ c_C   2nab 4 c³   8nabc

V = S (p) dp = —2 c2 + p2) dp = —(c2 p + ^)0 = — ■ c                   c           30 c     33

- c-

Javob:

8nabc

4-misol. Ushbu x4 + y4 = 4 x2 egri chiziq bilan chegaralangan figurani Ox o’q atrofida aylantirishdan hosil bo’lgan jism hajmini toping [2].

Yechilishi:

Berilgan egri chiziq tenglamasidan foydalanib, figuraning ko’rinishini hosil qilamiz:

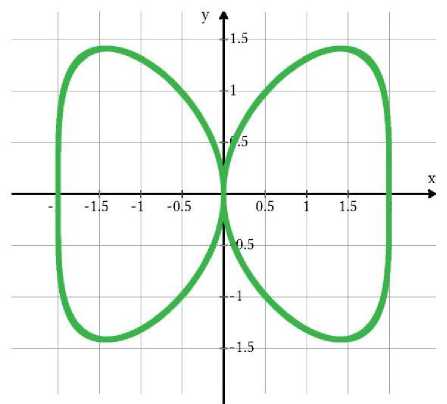
6-rasm

Rasmda (6-rasm) ko’rsatilgan D egri chiziqli sohani Ox o’q atrofida aylantirishdan hosil bo’ladigan jism hajmini hisoblaymiz [5].

Oshkormas ko’rinishda berilgan egri chiziq  tenglamasini quyidagi ko’rinishga keltiramiz:

y ² = 4 4 x ² - x⁴

Aylanma jism hajmini hisoblash formulasidan foydalanamiz:

20      0     0         3

16 п

V = п j y²dx = 2 п J 4 4 x ² - x⁴dx = 2 п j x 7 4 - x²dx = п j 44 - x²d ( x ²) = —(4- x ²) ² |0

- 2               - 2                         - 2                      - 2                        ³

16 п

Javob:

XULOSA

Aniq integrallarni ba’zi tadbiqlarini misollar yordamida o’rganish orqali matematika fanini boshqa fanlardagi tutgan o’rnini ham ko’rsatish mumkin. Masalan, ushbu maqolada ko’rib chiqilgan aniq integrallar yordamida aylanma jismlarning hajmini hisoblashga oid misollar nafaqat matematika fanida, balki fizika, kimyo va shu bilan birga texnikaning bir qator muammolarini hal qilishda ham uchrab turadi. Shulardan kelib chiqqan holda ushbu mavzu to’la yoritib berilishi orqali oliy ta’lim muassasalari talabalarining fanga bo’lgan qiziqishi, mantiqiy fikrlashi va muammoni kreativ yondashuv yo’li bilan hal qilish ko’nikmasini shakllantiriladi.