Axisymmetric bend of the lithospheric plate of the exponential profile

The plate tectonics model implies the stiffness of near-surface rocks and their elastic behavior at geological scales of time. Thin resilient surface plates form a lithosphere which floats on the underlying relative liquid mantle. The plates experience various loads, such as the weight of volcanoes and seamounts, so that they bend. For the study of such geological phenomena, the theory of bending of plates under the influence of applied forces and moments of forces is applicable. With this theory it is also possible to explain the occurrence of series of folds in mountain belts, as the formation of folds can be seen as deformations of elastic plates under the action of horizontal compressive forces. The theory of plate bending is used to simulate formation blasting over magmatic intrusions [1-3].

Objects and research methods

Consider axisymmetric bending of non-uniform elastic lithospheric plate of variable thickness of exponential profile in non-uniform temperature field by partial sampling method [4]. The basic differential equations of quasi-static equilibrium are reduced to the next second-order differential equation with respect to angular displacement

d 29 dr 2

-+

V ^r

1 dD M

Dm dr J

d9

--+

dr

^ ^_dDM_ -V rDM  dr   r2 J

9 +

rDrDM

( J q r rdr — c )

—

-+v d (XtDm ) = 0, DM dr

where           - angular movement,

Sr

– deflection, DM – cylindrical rigidity of a bend, – Poisson's coefficient, r – position of midplane point before its deformation,      – thermal deformation due to non-uniform heating, – intensity of cross forces.

An edge task is set when a circular plate of variable thickness with a rigidly embedded inner contour         is loaded along its outer contour

. Boundary conditions will take the form

, .

Let the plate be subjected to uneven heating. In the case of linear heat propagation a T in the thickness of the plate the thermal deformation is approximated in the form of

X t =   У ^Л ^ ₇r ⁷

h j = 0

In addition, let the plate of

variable

thickness rigidly embedded on the inner office r = r be loaded uniformly distributed along the surface by transverse forces of intensity q and along the contour r = r2 by transverse force Q n qz = У qjr, qz = qо j=0

q 1 = q 2 = q 3 ... = 0 , C = ^Qro ^{+ 0,5} q 0 ^r o² . (4)

Then the general solution of equation (1)

under an arbitrary law of change in thickness will be plate

-f ^ ( r ) dr

• 9 = B + A J e     dr +

  
  

• ^- ^SC^-dd r Л                                   ^- f ^ ⁽ r ) dr

+ I e      II [n( r) + ^( r) + ф(г) _e       dr I dr where

П ^(r) = - v У ln

D n ( Г к ) 9 ( r k - 1 )

DON

^r k — 1

^{M ( r} - r k — i ) - ln

D m ( r_k ) 9 ( r_k )

DON

^r k + 1

^{M (} r - r k )

—

—

У ¹ 9 ( r_k — 1 ) M ( _V ^r k J

. r - r k — 1 ^{) —}

1   1 dD

^(r) = -+       M ; ф(r) = r DM dr

Arbitrary coefficients A  and B are determined by boundary conditions (2).

By taking into account the first three members in (3) and the first member in (4), the

Л

— ^{9 ( r} k M ^r - ^r k ) ;

V ^r k J

^

1 + v d

DM dr

( X t D m ); f ⁽ r ) =- "^(J q z ^{rdr -} C ) . rD

M

general solution of equation (1) for the adopted plate stiffness law will take the form

к

—

Г Л

Δε

e

r

г	г	г
—	+ —	+
Г)	Г)	2

^{3 - о} 3 -

—

к

r ₀

r

, г г ln — + —

r ²

—

к ^Г о *^Г 0

36 r 0²

—

_h Dm ( - к ) S ( - к )

DOM

r ₀

—

к

rk

—

r ³

+--7

18 r 0 ³

r

r

r ⁴

+--

96 r 0 ⁴

r ⁵

+---

600 r ⁵

к

(1 + v ) r 2

+ - ln — + — +

r ²

r ³

к

к

r ₀

Зғ r0

36 - 2 ⁺ 486 - 3 ⁺ '"

r ³

V

h ₀

Δε ₀ r ₀

_{3 e} 3 r 0

+ -

+

486 r ³

rk e -оН (-

—

+ ...

rk

—

J i⁽ r ) i v Е ln

D m ( Г к ) S к — — 1 )

DOM

r ₀

_ ^-к — 1

^{e - о Н ( Г — -} к — 1 ^)—

л

- S ( Гк > ' H (

r —

к - 7

d S    , г

— = A — e

г

r ₀

dr

r ₀

г e-^ 1 Г)

Г к — 1

) +Е - ^ ( Г к — 1 ) ^— — ¹ e" ^Г 0 H (

к - 7

3 ^r

- ) к а о ^-^ e ^{к)     6} D о

-1 г

+ ^{(1 + v} ) Г e 5 - 7

^h 0 ^r

r ₀

г

1 + 2 - r ₀

—

r ₀

7 к

Г

к ^Г 0 7

\^{г — -} к — 1 ^{) —}

Qr ^{2 r}

+ e

D

г

г

3 ) Ле.

г

9 + ^{3 -} + 4 I Ле + - + 4

Г

LL 2  2 - о

D m ( Г к ) * ( - к — 1 ) _е

r ₀

к - о    2 7 - о

₊ q ^Г _e 3 D 0

r ₀

+ Q^ e

D 0

r ₀

—

D OM

r ₀

- к — 1

^{- о Н ( Г —} Г к — 1 ^)— ln

D m ( Г к ) S ( Г к ) _e

D OM

r ₀

rk

^{- о} Н ( г

—

Гк) +

—^{S (} Г к ) e ^{- о H ( Г}

Г к — 1

Е 7 S ( - - — 1 )- e "'H ( L< ^Гк 7         ^- о

r —

—

—

к   ^Гк

^Гк )

At that, from boundary condition (2) we get expressions for arbitrary constant

А = — 0,1713

q ₀ r ₀ ²

D 0

^— О,⁴¹⁷⁴⁵ Q^{- —} ^

^А ^ о

h ₀

—

3.034—- -А^, h0       1,

В = — 0,596

3 q ₀ r ₀

—

D 0

2,0235

Qr 0 ²

D 0

— 3,2633 ^— - А ^ — 5,о7757    - А ^ .

^{h h 1}

Bending moments defined by the following ratios

M- = Dm

d S   v п л \

~ + “S — (1 + v )хт dr  r

d S  1

МӨ = dm v-y + -S — (1 + v )х d-  -

Ө

M

T

>

will take a form

r

r

M — = d m ^

—

0,1713 ^{q 7 Г} ^- — 0,41745 ^QГ7- — 1,8552 ^{A s} 0

D 0

D

h

—

3.034 ^ ■

h ₀

л

r

A s , —e

r ₀

+

(1 + v ) —²    3 — 0

7 —0

^h 0 ^r

' 9   3 —   — ² V f —   3 ) Je,

+     +— Js . +1+—

3 r

r

r

2 r ₀

^— 0 7

r ₀

₊ q 0 Г 2 _e

r

r ₀

r ₀

3 D 0

+ ^Q— e

D 0

r

r ₀

r

r

—

e

r ₀

r ₀

< v Z h

D m ( — k ) S ( — J

r k — i

^D OM

r ₀

e

^—) H ( —

—

r k —1 ^ ln

D M ⁽ r k ) ^ ( r k )

DOM

r ₀

rk

e

^{— 0} H ( — — — k ) +

Z -S ( — k —1 )

.1 ^— k 7

v

—

r

—

0,596

+

—

X

0,1713

r

rk

r k — i

^{Г k} - ¹ e ^Г0 H (

r

—

—

r ₀

q ₀ r ₀ ²

D 0

q ₀ r ₀ ²

D 0

r

—

—

- ^( —k )e Г0 H(— — —k)

r

2,0235 ^{Q— 0} — 3,2633 ^—^ A s

D 0

h

—

>

—

\

—

5,07757 — 0- -A s + h 0        ¹

0,41745 Qr^ — 1,8552^ — 3.034 ^— --A s 1 —₀ ■

D

h

h

r r r ln — + —+ —r +

r

X

r ₀

r ₀

4 r ₀

18 r 0

+

r

96 r ₀

+

r

600 r

r

\

+ ...

+

^{(1 + v} ) — 2

h ₀

< Ле_х

e

3 r ₀

3 ^—

—

X

r ₀

r

r

+ - ln — ++

X

r ₀

3f r ₀

r

36 r ₀

+

r

486 r

+ ...

+

Δε ₀

r ₀

—

_{3 e} 3 r 0

r

r

+ ⁹ ln- + —

—

r

X

r ₀

3f r ₀

36 r ₀

+

r

\

486 r

+ ...

—

J; ( — ) V Z ІП

D M ( — k ) S ( — k — 1 )

r k — 1

—

ln

—

DOM

r ₀

e

^{— 0} H ( —

—

r k — 1 )

—

D M ( — k ) X — k )

DOM

r ₀

—

X

\

rk

e

^—0 H ( —

—

\

— k ) +z - ^ ( — k — 1 ) ^{— k —}^

r

e

^— k — 1

X ^—k 7

r ₀

^—0 H ( —

—

^—k — 1 )

—

\

rk

- ^ ( — k ) e ^{— 0} H (

r

—

^—k 7

—k) к

^q 0 ^r 0 ³

6 D 0

r

e

r ₀

r

1 + 2 —

r ₀

—

r

\

Qr

+ —— e

r

r ₀

—

—

М ө = d m ^

—

"7

(X

X ^— 0 7

D 0            D 0          h 0

—

D 0

■ ⁽1 ^{+ v} ) ^{1 (A s} 0 ^{+A s} 0 ^— ) > h

r

r

e

r ₀

+

r

^{(1 + v} ) ^— e I—⁷»

7 ^— 0

^h 0 ^r

r

r

+ ^q o ^Г_Le^— 0 + 5^—) e

r

+   +    Js , + -+ ³ 1 ^Js

r

r

X

^— 0 7

X ^— 0

3 D 0

D 0

r ₀

r

—

e

r ₀

^— k — 1

V

^D OM

e —0 H (—

—

^— k — 1 ) - ln

^D OM

rk

r

^— k — 1

r

—

X ^— k 7

^— k — 1 ^)—

—

X

rk

- S ^{( —} k ) e ^{— 0 H ( — — —} k ) >

—

— k 7

—

+

г

к

r

г

—

к

—

0,596 ^{q 0 r 02} D 0

0,1713 ^{q 0 r 02}

^,       D 0

—

—

2,0235 Q 0- — 3,2633 r Д ^

^D 0           ^h 0    ⁰

0,41745 Q i — 1,8552

^,         D 0     ^,

—

—

к

I 5,07757 1 -Д^ + h0      1

r

r

r

rrrr

ІП--11--— +7 +

4r0218

r ⁴

h

r ₀

r ₀

96 r 0 ⁴

+

r ⁵

600 r ₀ ⁵

r

—

г

Δε

г

e

ln ^r

к

r ₀

—

ln

—

r

³ r ⁰ 3 ^r

—

С

r

к

r

+ —

3f

3 r ₀

r ₀

—

r ²

36 r 0 ²

D m ( r_k ) ^ ( r )

DOM

r ₀

rk

—

—

к

9 r

+ - h-

+

r

к

r ₀

+ — +

3r r0

r ³

486 r ₀ ³

+ ...

—

rk

•-----------

—

e

r ⁰ H ( r

—

3.034r -Д^ Ir -

+... 1 +

r ²

36 r 0 ²

+

h ₀

(1 + v^-

h ₀

r ³

486 r ₀ ³

+ ...

₊ ^s 0

r ₀

3 e³ r ⁰ + ⁹

J 1 ^{( r} К V Z ln

D m ( r ) * ( r —1 )

^D OM

r ₀

r k ) +Z f- Ъ ( r k —1 ) r e r ⁰ H ⁽ r

Ьк ^r k

r ₀

—

—

r k —1 —

e r ⁰ H ( r

r_k —1 )

—

—

r k —1 )

—

¹ k ( r k ) e r ⁰ H (

—

r

—

rk

rk) [ + qr3 e k ’    6 D 0

r

r ₀

r

1 + 2 -

r ₀

—

с

r

к ^r 0

Qr

+     e

D 0

r

к

r ₀

—

(1 + V )1 (Д'0 +Д'0 r )'

Results and their discussion

The application of the partial sampling method has made it possible to solve the problem for any law of changing mechanical characteristics. On the basis of the found solution and numerical analysis for stress-deformed state of the lithospheric plate under the action of radial uniformly distributed load and volumetric centrifugal forces, as well as a result of temperature heating, patterns of change of radial force and bending moments are found, which are shown in the form of graphs in Figures 1-2.

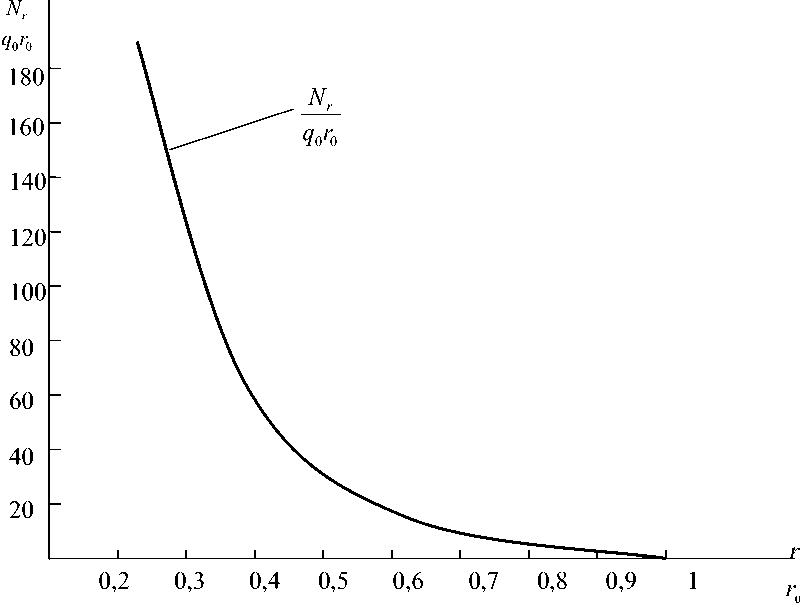
Figure 1 - Regularity of radial force N distribution under action of longitudinal radial intensity q force

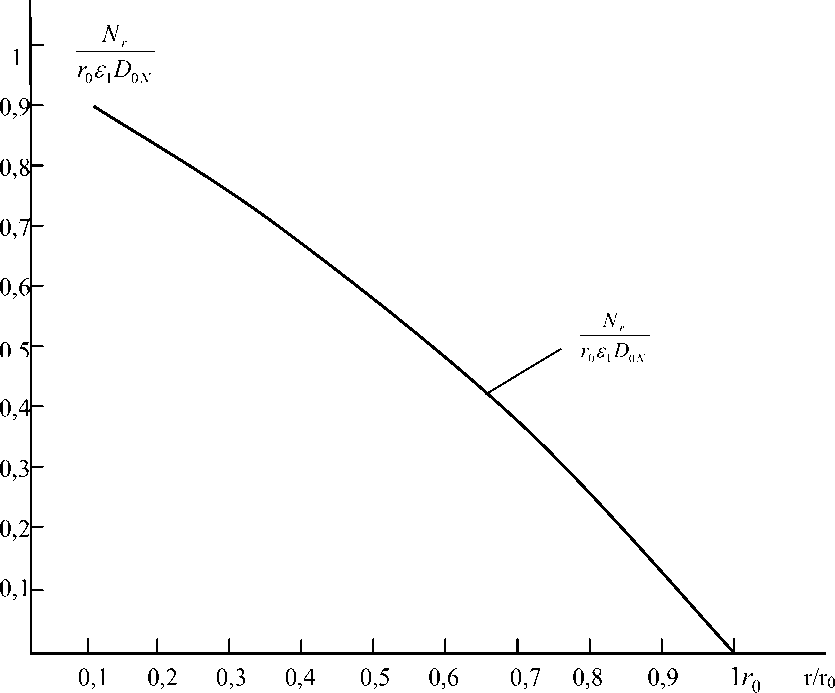
Figure 2 - Law of change of radial force of the plate subjected to temperature heating

Conclusion

New model of stress-strain state of axisymmetric lithospheric plate of exponential profile in non-uniform temperature field and under action of transverse forces is proposed.

To solve the nonlinear differential equation with non-uniform bending coefficients of the lithospheric plate, the partial sampling method was applied for the first time.

Obtained regularities of change of radial force and bending moments under action of radial uniformly distributed load and volumetric centrifugal forces, and also as a result of temperature heating characterize stressed-deformed state of plate. Graphical analysis indicates the nonlinear nature of their distribution.