Численное моделирование диффузии в средах с ловушками: статистика в одномерном случае

Исследование выполнено за счёт гранта Российского научного фонда № 2421-00356,

Проблема диффузии частиц в средах с поглощающими ловушками изучалась во многих работах [1–2]. Интерес обусловлен как различными приложениями, так и аналогией с проблемой плотности состояний в неупорядоченных средах [3], а также ожидаемыми новыми особенностями в транспорте частиц [4–8]. В работе [9] описаны результаты численного моделирования процессов захвата частиц на ловушки.

В настоящей работе продолжено исследование стохастических процессов в средах с ловушками, в частности, исследована зависимость характерных времен захвата на ловушки от концентрации ловушек. Как известно, в различных физических явлениях как правило возникают характерные параметры, описывающие эти явления. Например, в теории фазовых переходов – это корреляционные длины физических восприимчиво-стей и т.д., в случае динамических процессов — это характерные времена процессов. В случае диффузионных процессов появление таких параметров неочевидно, тем не менее они появляются. В задаче диффузионных процессов в средах с ловушками возникает характерная длина – расстояние между ловушками и, соответственно, в динамике время диффузии на расстояние порядка длины между ловушками. В одномерном случае оно равно:

tc

Dc ²

Здесь D — коэффициент диффузии, а c — концентрация ловушек, в одномерном случае расстояние между ловушками равно обратной концентрации. Одной из задач статьи является определение указанного физи- ческого параметра.

Статья построена следующим образом. В первом пункте статьи описаны алгоритмы и методы численного моделирования, а также приводятся характеристики посевов ловушек. В втором пункте изложены основные результаты численного эксперимента. В заключении обсуждаются результаты и производится сопоставление с известными теоретическими выкладками.

1    Алгоритмы и методы численного моделирования

В настоящем параграфе коротко опишем алгоритмы и методы моделирования, опишем постановку численного эксперимента. Для исследования описанных процессов было выполнено численное моделирование процессов захвата частиц на ловушки.

Введем основные определения. Рабочей областью будем называть отрезок на числовой прямой [-500000, 500000]. Ловушкой будем называть точку на числовой прямой, при попадании в которую частица «умирает», то есть перестает участвовать в итерациях и не меняет координаты.

Перед началом работы на рабочую область размещаются ловушки из заранее подготовленного посева. Далее происходит первоначальный посев частиц. Частицы размещаются на рабочей области произвольным образом, при этом координаты частицы не должны совпадать с координатами ловушек.

Итерацией алгоритма будем называть разовое смещение всех частиц. Частица может сместиться вправо или влево на 1. Направление смещения определяется случайным образом, вероятность — одинаковая.

В рамках одного запуска алгоритма происходит N итераций. После завершения алгоритма происходит запись координат выживших частиц, а также формируется информация для итогового протокола, в котором фиксируется число выживших частиц.

Эксперимент представляет собой серию запусков алгоритма с фиксированными параметрами для разного числа итераций, по результатам эксперимента формируется протокол эксперимента. Эксперименты проводились со следующими начальными значениями:

• 1.    Количество частиц: M 0 =100000

• 2.    Количество итераций: N= 1000 - 200000

• 3.    Шаг (изменение количества итераций): dN = 1000

Протокол эксперимента включает в себя описание начальных значений, использованного посева, а также информацию о числе итераций и количестве выживших частиц.

1.1    Посевы ловушек

Было сгенерировано 11 посевов ловушек на рабочей области ([-500000, 500000]).

Посевы генерировались следующим образом:

• 1.    Задавалось число ловушек K - от 5001 до 15001 (с шагом в 1000)

• 2.    Для каждой ловушки в рабочей области генератором случайных чисел определяется координата. Если эта координата не занята (нет ловушек с такой координатой), то в нее помещается ловушка, если занята, производится повторная попытка, пока не будет получена свободная координата для ловушки.

• 3.    В итоге получаем посев, который представляет из себя K координат ловушек.

Можно сказать, что ловушки разделяют рабочую область на отдельные интервалы. Предлагается характеризовать посевы следующим образом.

Для каждого интервала вычисляется длина, после чего подсчитывается количество интервалов такой длины. Пример характеристики для посева с

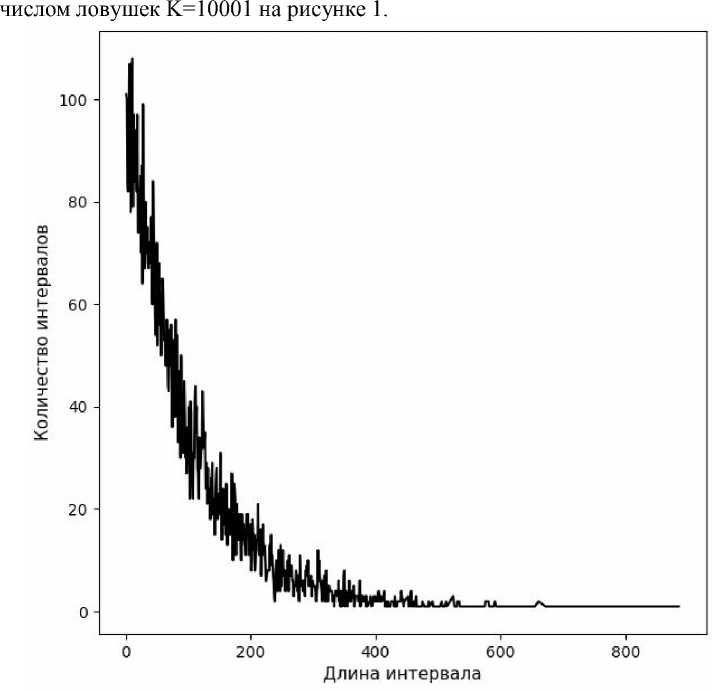
Рисунок 1. Характеристика посева ловушек (K=10001)

На рисунке по оси абсцисс располагаются длины интервалов, по оси ординат — количество интервалов такой длины. Для разного числа ловушек описанная характеристика имеет схожий вид. На рисунке 2 пример

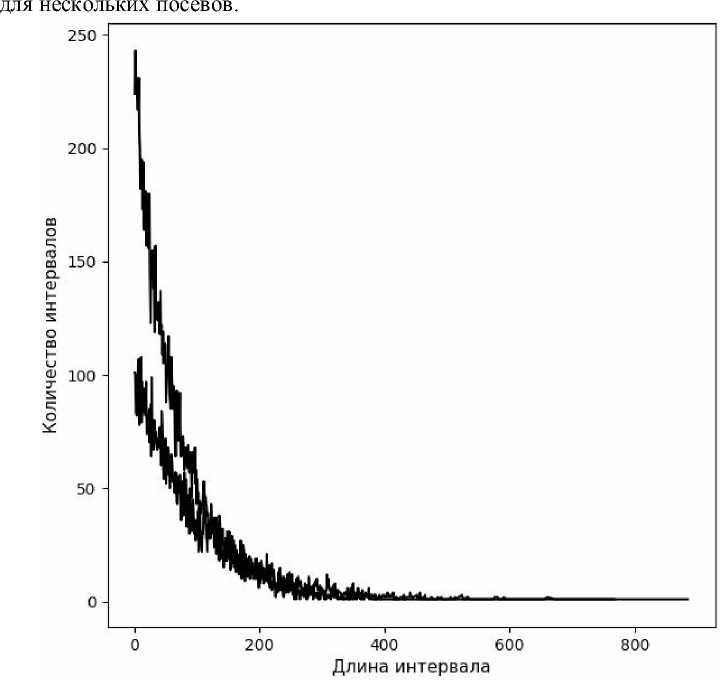
Рисунок 2. Характеристики посевов ловушек (K=10001, 15001)

На рисунке приведены характеристики посевов с K=10001, 15001. Очевидно, что при увеличении числа ловушек увеличивается количество интервалов с меньшей длиной и уменьшается максимальная длина интервала.

2 Результаты

Для каждого из описанных посевов были проведены численные эксперименты, которые включали в себя серию из 10 запусков для каждого посева ловушек. Результатом каждого запуска является отчет с данными о числе «выживших» частиц, то есть о частицах, которые не попали в ловушки. На рисунке 3 представлены графики изменения числа выживших частиц для разных посевов ловушек.

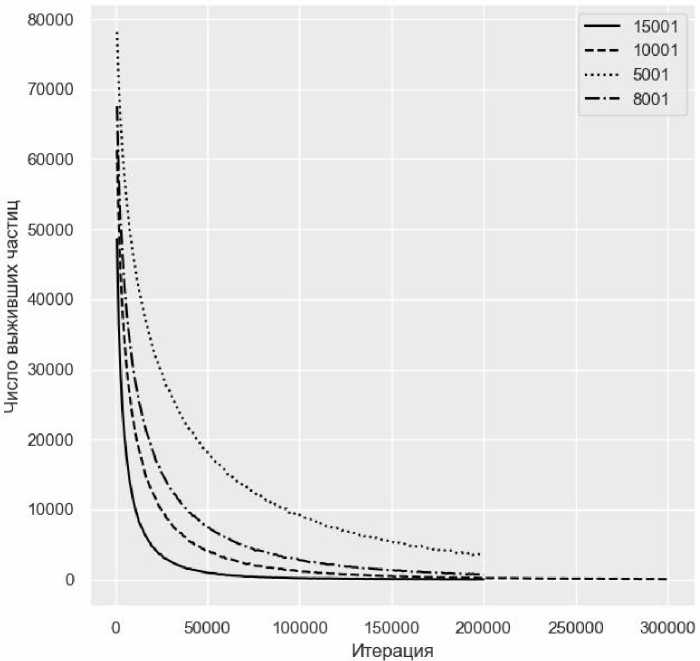
Рисунок 3. Зависимость количества выживших частиц от количества итераций

На рисунке 3 представлены графики зависимости количества выживших частиц от количества итераций для посевов с числом ловушек: 5001, 8001, 10001, 15001. Очевидно, что при увеличении числа ловушек, число выживших частиц будет уменьшаться быстрее. Для наглядности рассмотрим логарифмическую зависимость (рисунок 4).

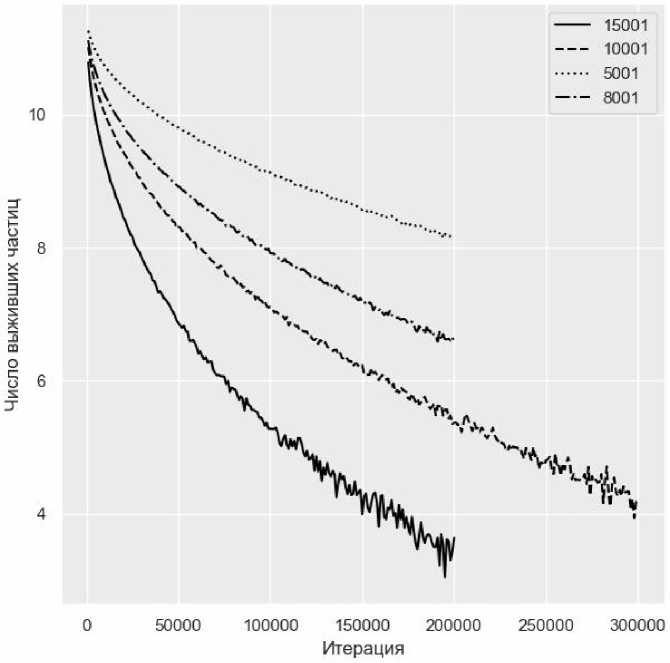
Рисунок 4. Зависимость логарифма числа выживших от количества итераций

На рисунке 4 представлена логарифмическая зависимость числа выживших от количества итераций. При увеличении числа итераций можно заменить явные флуктуации на графиках, особенно для большего числа ловушек в посеве, этот факт можно объяснить тем, что при большом числе итераций выживает мало частиц и количество активных частиц варьируется за счет «случайности» процессов. В рамках исследования для каждого посева было произведена серия из 10 запусков. Таким образом, для выявления закономерностей логично рассматривать усреднённые значения.

Результаты каждого запуска являются массивом пар чисел (x, y), где х — число итераций, а y — количество выживших частиц. В качестве генератора случайных чисел был использован «Вихрь Мерсенна», следовательно, можно говорить о том, что распределение было нормальным. Усредненным протоколом для посева ловушек будем называть протокол, строки которого представляют собой пары чисел — число итераций и среднее от количества выживших частиц, полученные из 10 файлов протоколов для соответствующего посева ловушек. На рисунке 5 представлен график усредненных данных (логарифм).

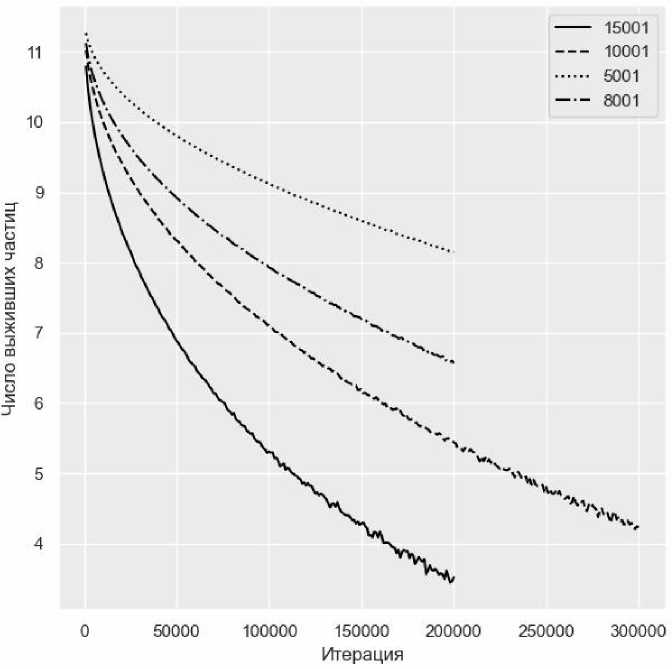
Рисунок 5. Логарифм числа выживших от количества итераций (усреднённые)

На рисунке 5 приведён график усреднённых протоколов для посевов, отображённых на рисунке 4. Визуальное сравнение графиков позволяет говорить о том, что усредненные данные сохраняют характер поведения. При этом усреднение «сглаживает» флуктуации, вызванные случайностью самих процессов.

В целом, анализ полученных графиков позволяет говорить о характерном «поведении» для разных посевов ловушек. В связи с этим возникает необходимость исследования данного явления с учётом статистики экспериментов.

Для исследования характера зависимости вымирания частиц введем понятие — время вымирания. Временем вымирания будем называть количество итераций при котором число частиц становится меньше исходного числа в e раз (обозначим его yDie). В нашем случае это число будет равно: 37037 (100000/e).

Протокол исследования содержит информацию о количестве выживших частиц в зависимости от числа итераций. Шаг по числу итераций равен 1000. Усредненные данные эксперимента позволяют определить отре- зок, на котором происходит «вымирание», для вычисления точного времени вымирания была использована линейная интерполяция:

• 1.    для каждого посева рассматривается усредненный протокол;

• 2.    в протоколе находится первая строка, в которой число выживших меньше yDie. Обозначим эту пару значений из строки: (x[n],y[n]), здесь n — номер строки в протоколе.

• 3.    по парам (x[n-1],y[n-1]),(x[n],y[n]) вычисляются коэффициенты аппроксимирующей прямой y=Ax+B.

• 4.    определяем время вымирания (xDie) из уравнения yDie = Ax+B.

На рисунке 6 представлен график зависимости времени вымирания от числа ловушек:

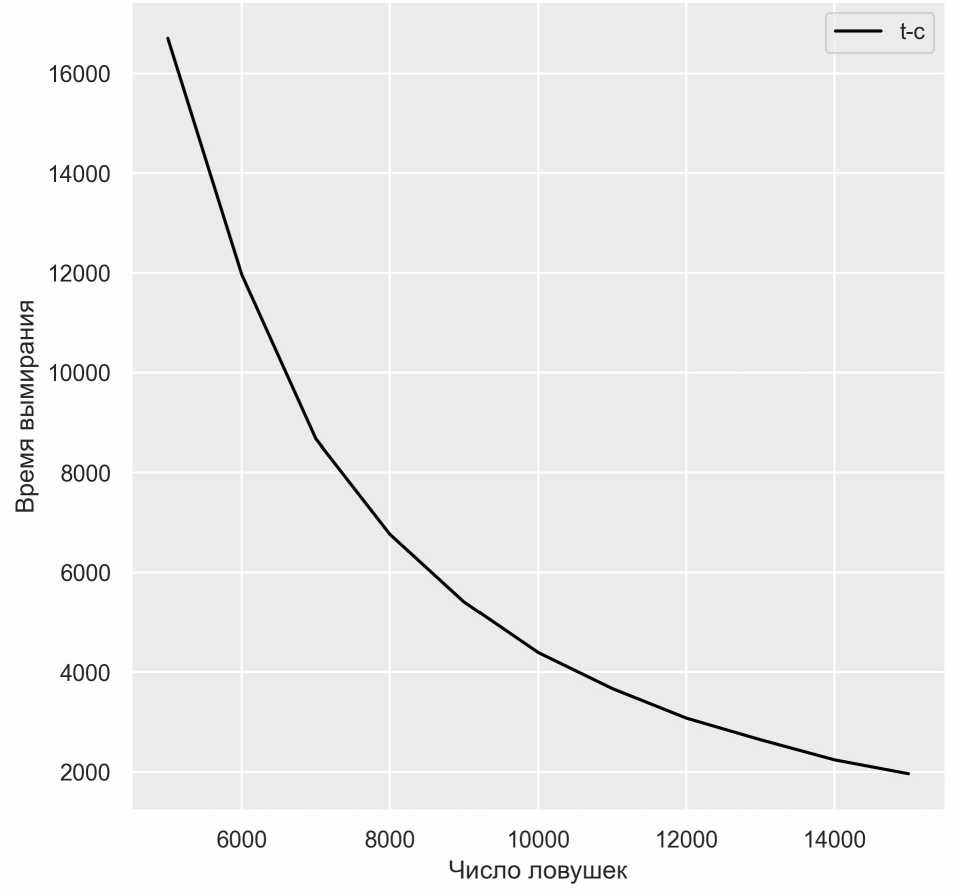
Рисунок 6. График времени вымирания

Визуальный анализ графика позволяет говорить о явной гиперболической зависимости. Согласно теоретическим выкладкам зависимость времени вымирания от числа ловушек должна аппроксимироваться гиперболической зависимостью [10, 11].

Была проведена аппроксимация функциями вида:

• y = a + b .                                 (2)

alpha x

При аппроксимации рассматривались фиксированные значения для параметра alpha, коэффициенты ( a , b ) вычислялись методом наименьших квадратов. На рисунке 7 представлены графики аппроксимирующих кривых.

6000        8000       10000       12000       14000

Число ловушек

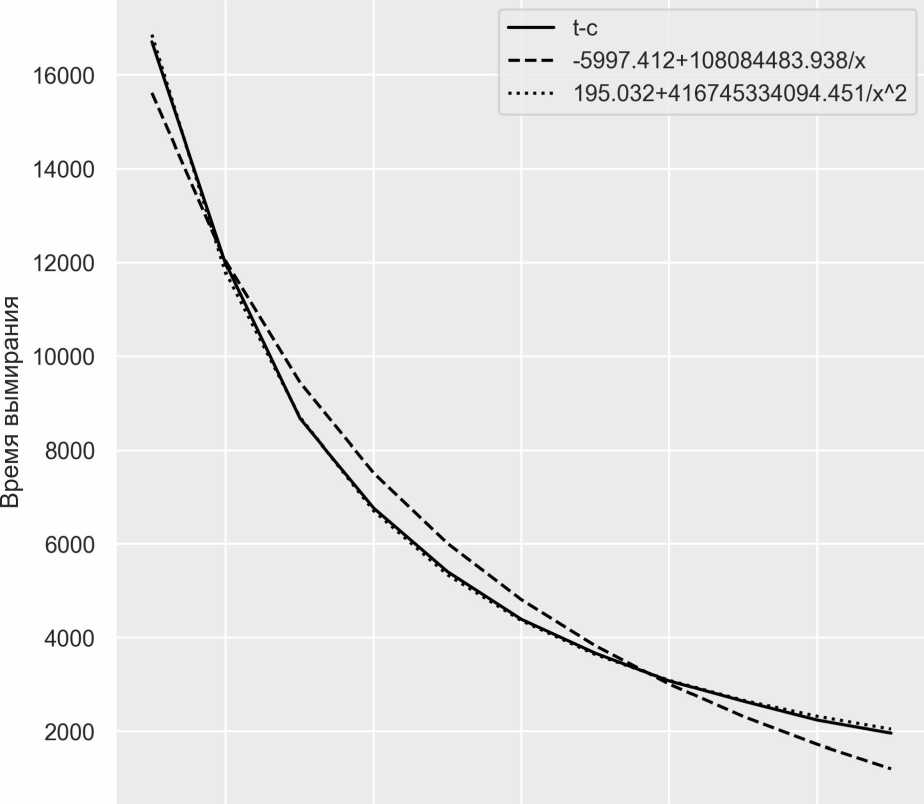
Рисунок 7. Аппроксимация времени вымирания

На рисунке 7 сплошной линией обозначен исходный график, пунктиром — аппроксимация гиперболой, точками — аппроксимация квадратичной гиперболой. В легенде представлены коэффициенты. Визуальная оценка подтверждает теоретические выкладки — график квадратичной гиперболы практически совпадает с исходным графиком.

При использовании формулы средней абсолютной ошибки аппроксимации были получены результаты: 11,633 % — линейная гипербола, 1,417% — квадратичная гипербола. В общем стоит отметить, что при повышении степени гиперболы от 1 к 2 средняя ошибка аппроксимации уменьшается, что подтверждает теоретические выкладки.

Заключение

Обсудим полученные результаты. В настоящей работе выполнено численное моделирование процессов захвата на ловушки частиц, диффундирующих в средах с ловушками. Было сгенерировано одиннадцать случайных посевов ловушек с числом ловушек от 5001 до 15001 (шаг 1000). Для каждого посева была проведена серия из десяти экспериментов и сформирован усреднённый отчёт.

Общий анализ изменения количества выживших частиц в зависимости от числа итераций соответствует и подтверждает полученные ранее результаты. Для более глубокого анализа изменения количества выживших частиц в зависимости от количества итераций было использовано понятие «время вымирания». На основе усреднённых отчётов была построена зависимость времени выживания от числа ловушек.

На рисунке 6 приведён график изменения времени вымирания. Визуальный анализ позволяет говорить о гиперболической зависимости. Данные были аппроксимированы гиперболическими функциями вида b y = a +—— • Наилучшие результаты были получены для квадратичных x функций, что подтверждает теоретические выкладки.

Исследование характерных времен в задаче важно для дальнейших исследований. Во-первых, как правило, на малых временах работает приближение «среднего поля», однако на временах больших характерных времен задачи появляются новые функциональные зависимости, так называемые флуктуационные, которые обусловлены нарушением приближения «среднего поля» [12, 13]. Во-вторых, в случае появления в задаче еще одного параметра, как в задаче с внешними полями, можно ожидать также новых закономерностей в областях, когда новый параметр превышает исходное время диффузии [14, 15]. Поэтому проведение выше описанных численных экспериментов позволит определить область поиска новых закономерностей и функциональных зависимостей.