Criterion of absolute stability of control systems

Негізгі сөздер: белгі, тұрақты, реттелетін жүйелер, тепе-теңдіктің жағдайы.

The modern theory of control systems has powerful methods to analyze and design complex systems of computers, aircraft, energy facilities and automatics. Control systems belong to a class of dynamical systems with feedback, for which we study the stability and quality of transients, dynamic accuracy, self-oscillations and the problem of synthesis and identification.

At present the research of absolute stability of nonlinear systems is based on two approaches:

• 1)    A.I. Lur’e’s method [1], based on a choice of a Lyapunov function in "the square-law form plus integral from nonlinearity ";

• 2)    The frequency criterion of absolute stability by V.M. Popov [2].

The frequency theorem V.A.Yakubo-vich’s [3] has shown direct interconnection between these approaches, namely, the frequency criterion of absolute stability is a necessary and sufficient condition of existence of the above-stated function Lyapunov function and, guarantees the presence of the real solutions of the permitting nonlinear Lyr’e equations.

The verifications of the frequency criterion is the main problem in the theory of absolute stability. In other words, the fre-quency criterion of absolute stability is redu-ced to establishing of analytical conditions of absence of positive roots some polynomial.

Many works have been devoted to investigation of this problem. The work of M.V. Meerov [4] is based on the D-spliting method, the work of S.A. Aisagaliev [5] is based on Sturm theorem, and the study of D.D. Silyak [6] is based an applicaition of critical cases of the Routh- Hurwitz. In [7] the author has obtained a cjndition of positivity of a certain polynomial without using Sturm theorem.

Statement of the problem. Let us assume that the control system is described by the differential equations of the following form x = Ax+bgp),p = cx, x(0) = x0, t e[0,да), where A is constant nxn matrix, b,c are vectors of dimension n. The nonli-nearity «Дп ) satisfies the condition

0 <  ^^ ) / p <  ц , ^ ( 0 ) = 0 .

The nonlinear system (1), (2) in operator form is written as

P = W ( p )[ - ^p )]

where W ( p ) = c ' ( A - Ep )^{- 1} b is transition function, p is a complex variable, E is a unity nxn matrix.

We introduce the following notation: let p_i ( A ) be eigen values of the matrix A , p_i ( f ( p )) be the roots of polynomial f ( p ) of degree n , i = 1,..., n . We say A is a Hurwitz matrix if Re p i ( A ) л 0 , i = 1,..., n and we say that f ( p ) is Hurwitz polynomial if p, ( f ( p )) л 0 , i = 1,..., n .

In the theory of absolute stability the cases are considered, when the own meanings of a matrix A lay in left plane (main case), and in critical cases the matrix besides the above-stated own meanings can have only imaginary and zero.

For critical cases the transition function W ( p ) is presented in one of the following forms

W(p) = — + X( p) p

W (p )= ap в2 + X(p) p + ®0

^{W (} p ) = ^{p +} ^ p r ^ ⁺ x ⁽ p ) p p + ® 0

W (p ) = P + p- + X( p ) pp

The main case. The absolute stability of a rule of balance x=0 of system (1) with nonlinearity (2) is established frequency criterion

n(to) = Re(1 + itoS )W(ito)+ ц—1 > 0 VtoE(—x,x)

where v is the Popov constant.

Critical cases. Frequency criteria of absolute stability in view of transition functions (4) - (7) accordingly look like:

n(to )= Re(1 + itoS) x( ito) + Sp + ц1 > 0 VtoE (-x, x), py 0,(9)

n(to )       =       Re(1 + i to ^в 2 ) x ( i to ) + -^ + ц ¹ >  0 VtoE ( -x , x ), a у 0, в >  0

αω02

n(to) = Re(1 + ito в2)x(ito) + -Д- + рв + ц 1 > 0 Vto e (-x,x), a у 0,в > 0

αω ₀        ω ₀ αω ₀

n ( to ) =    Sp + S Re itox ( ito ) >  0      V to E ( -x , x )    , p ^ 0, р 1 у 0

The decision of task. Transition function of operational equation (3) shall copy as a (p)   is m < n — 1 , E is the unity nxn matrix.

First, we consider the main case, when a A is Hurwitz matrix. Let's enter any polynomial

5 ⁽ p )

with the real coefficients and degree n. It is supposed, that poly-nomial’s s(p) , b(p) are

W ( p ) = c ‘ ( A - p E )^{- 1} b

a(P) b(p)

mutually simple.

Definition. If

where b ( p ) = A -E p | is the characteristic polynomial, the degree of the polynomial

Re ^ ( p ) >  0 ( > 0 ) V Re p >  0     (14)

b(p)

then the real part of rational function is called positive (non-negative). Then is fair Lemma. Let b(p), s ( p ) be Hurwitz polynomials and the polynomial 5 ( p ) b ( - p ) has no roots on the imaginary axis. Then the inequality (14) holds. The proof. Necessity. The coefficients of Hurwitz polynomials b ( p ) , 5 ( p ) are positive: b i >  0,    s i >  0, i = 0,1,..., n (15) Therefore the inequality (14) is true for V Re p >  0. Sufficiency. It is necessary to check that the inequality (14) on the imaginary axis Im p = to (Re p = 0), to e ( — да , да ) . For of ( real and imaginary parts of the rational function we write determining 5 ( p ) = A 0 ( — p 2 ) + pa i ( — p 2 ) b ( p ) B 0 (— p 2 )+ pa i (— p 2 )             . (16) A 0 B 0 + XA , B , , A 1 B 0 - 4 B 0 ( Re b (20) coprime. The latter means that the algebraic equation f ( p ) = 5 ( p ) b ( — p ) = 0 (21)

Multiplying by B 0 — pB 1 the numerator and the denominator of the rational function, we obtain 5 ( p ) _ 4 B 0 + XA , B Re b ( p ) = B 02 + x b                , (17) X    5 ( p ) _ 4 1 B 0 — A 0 B 1 p   b ( p )    B 02 + X B           , (18) where X = — p 2 , p = ito. . Hence, it is necessary to check the absence of positive roots of the polynomial g ( X ) = A 0 ( X ) B 0 ( X ) + X A 1 ( X ) B , ( X ) > 0 V X >  0       . (19) As the denominator obviously is positive: b ( ito ) b ( — ito ) >  0 V to е ( —да , да ) . This is possible if the polynomials ( p )   li m 5 ( p )) ( p )    , p    b ( p ) ) has no roots on the imaginary axis, or, equivalently,

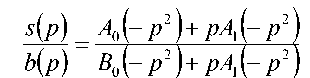
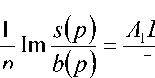
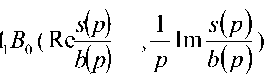
A m =	f 1 f 0..... f 3 f 2 f 1 f 0.....	^ 0 , m = 2 n . (22)
	f f .........f J 2 m - 1 J 2 m - 2        J m

The latter condition is easily checked using the Routh-Hurwits criterion. Lemma is proved.

The lemma is easily transfered to critical cases (4) - (7).

We considers polynomial

• 5 (p ) = (yp + 1) a (p ) + Ц-1 b (p ) (23)

which is connected to frequency criterion (8) and transition function (13).

• Theorem 1. Let

• ^{5 (} P ) = k^Sp ⁺ 1 ) ^{a (} P ^{) +} ц ¹ b ( p ) be the Hurwitz polynomial and the conditions of the lemma holds then the criterion of absolute stability (8) holds. Proof. According to the conditions of theorem the inequality

Re SW = Re d ⁺ S p ) a ⁽ p ) ^{+ Ц} -' ^{b (} p ) ^ 0 V Re p ^ 0 b ( p )                 b ( p )

is equivalent to

_Re ⁽¹ + ^{S p} ) a ^{( p} ) ₊ ц -i ^ о v R_e p >  0 . b ( p )

If Re p = 0 that the latter inequality can be rewritten as

Re(1 + iwS) a ⁽ iw ) + ц >  0 V w e ( -» , +» ) b ( iw )                          ^,

Thus, the conditions of the lemma are fulfilled and the frequency criterion of absolute stability (8) holds. The theorem is proved.

Theorem 2. If 3 the parameter S , and, therefore s ( p ) is a Hurwitz polynomial and the polynomials A 0 B 0 + XA 1 B 1 , A 1 B 0 - A 0 B 1 are relatively prime, then the equilibrium x = 0 of the system (1) with the nonlinearity (2) is absolutely stable. Proof. Using (23), (14) is rewritten as

Re ^ ( p ) = Re d ⁺ S p ) a ⁽ p ) ^{+ Ц - 1 b (} p ) ^ 0 V Re p >  0 , b ( p )                 b ( p )

where a( p), b(p) are the numerator and the denominator of the transition function (13), by the condition of the main case b(p) is Hurwitz polynomial. The conditions of the lemma are satisfied. This means that the inequality (19) holds, implying respectively the frequency criterion for absolute stability (8) for some parameter valueϑ . Thus, the equilibrium x = 0 of the system (1), (2) is absolutely stable. The theorem is proved.

Similar theorems are obtained for the critical cases that are not included in this work due to a limited extent.

Thus, the new criterion of absolute stability is formulated as follows:

if 5 ( p ) = 9p + 1 ) a ( p ) + ц ^{- 1} b ( p ) , b ( p ) are Hurwitz polynomials and polynomial 5 ( p ) b ( - p ) has no roots on the imaginary axis then the system (1),(2) is absolutely stable. Formulas (22) and (23) solve a problem of Aizerman.

We show the advantage of a new criterion of absolute stability. It should be noted that for the system (1), (2) of the third-order of until now analytical conditions for absolute stability were not obtained. Let the transition function of system (1), (2) is given in general form a о p + ax p + a 2

W ( p ) =

b 0 p ³ + b 1 p ² + + b ₂ p + b 3

Then

5 ( p ) = (9a 0 + ц 1 ) p ³ + (9a 1 + a 0 + ц ¹ b 1 ) p ² + (9a ₂ + a 1 + ц ¹ b 2 ) p + a ₂ + a 3 , b ( p ) = b 0 p ³ + b 1 p ² + b ₂ p + b 3 .

The lemma implies that A0B0 + XA1 B1 and f (X) = X3 + aX2 + bx + c, h (X) = X + dX + e

A 1 B ₀ - A ₀ B 1 are coprime ^

have no common roots,

where a =

s ₀ b ₁

^{- 5} о b 2 ^{- 5} 2 b b

^S 0 ^b 0         ^,

⁵ 2 ^b 2 ^{- 5} 3 ^b 1 ^{- 5} 1 ^b 3

S 0 b 0

s ₃

^S 0 ^b 0 ^,

d = 'b

^{- 5} 2 ^b 0 ^{- 5} 0 ^b 3 ^{- 5} 2 ^b 1

⁵ 2 ^b 3 ^{- 5} 3 ^b 2

S 0 b 1 - S 1 b 0 ’

The discriminate of the polynomial f ( λ ) is D = a ² b ² - 4 b ³ - 4 a ³ c + 18 abc - 27 c ².

Theorem 3. Let b(p) be a Hurwitz polynomial and assume that there exist ϑ such that 5(p) is Hurwitz polynomial, D < 0. Then if c + ae > 0 , a - d + a ^ 0 or c + ae < 0 , a - d + a > 0 then there exists a negative root of f (λ) denoted by α , and, therefore , the nonlinear system (1), (2) of the third-order absolutely stable.

Proof. If D < 0 that polynomial f (X) = X3 + aX + bx + c has one real and two complex roots. We show that there is a negative root α of the polynomial f (λ) which can be written as f (X) = (X - a)h(X) + r(X),

	statement inequalities of the theorem follow. If D >  0, it is sufficient to a >  0, b >  0, c >  0.
where r ( Л ) _ ( a - d + a ) Л 2 + ( b + ad - e ) Л + c + ae .	Thus, the nonlinear sys-tem (1), (2) of the third-order absolutely stable.
A negative root α of the polynomial r ( λ ) exists if	It is easy to extend the conditions of Theorem 3 to system (1), (2) of the fourth order.
c + ae д      <  0, a - d + a	A classic example V.A. Pliss. We carry out the study of absolute stability of nonlinear system in [9] to solve the problem Aizerman, in with 0 <  ц lyap ^ 1, 0 <  ц киг ^ 2. The linear part
where h(a ) ^ 0. From these conditions of the	of the system(1) is characterized by the transition function (5):

W ⁽ p >pp^

_ 0.75 p - 0.75  0.25

p2 +1 p +1, and the nonlinearity satisfies the condi-tion (2). It is easy to show that a closed linear system has the characteristic equation:

which is based on the frequency criterion (10) for the critical case. Here f (p)_ p 3 + (1 + Ц)p2 + p + (1 — 0.5ц)_ 0

max

β αω ₀ ²

^{- 1},

X(p) _

0.25

p + 1

and f ( p ) is Hurwitz polynomial changing from zero to two. We investigate the absolute stability of the system using the polynomial (23):

For absolute stability of the nonlinear system in the critical case it is sufficient to check that the

s ( p )

is Hurwitz polynomial for

s ( p ) _ ( ц ¹ - 1 ) p + ц ¹ - 0.5

⁰ <  Ц = Ц lyap <  Ц тах = ^{1 .} This result is entirely

consistent with the results Pliss.

A classic example of D.D. Siljak ( the main case). For system (1), (2) the transition function

W ( p ) =

p ²

0.2( p ³ + 6 p ² + 11 p + 6),

.0 <  ц <  1, 9 _ 0.

To check the conditions of the theorem 3 we calculate the coefficients of the polynomials f (λ) and h(λ) and find that a _ 44 , b _ 49 , c _ 6 , d _ -12.2, e _ 0 . Liner inequalities of the theorem are satisfied if a < -56.2, h(a) * 0. The system is absolutely stable.

Thus, the reliability of the results is verified by the study of classic examples of Pliss and

Siljak. To summarize,

• a)    set a new criterion of absolute stability, which is a necessary and sufficient condition for the existence of a frequency criterion of absolute stability by V.M. Popov;

• b)    the first time, the analytical conditions for absolute stability of nonlinear control system of the third order are obtained;

• c)    the explicit analytical conditions for the solvability of problem Aizerman is obtained.