Дидактический процесс прикладной математической подготовки в условиях непрерывного образования «школа - технологический университет»

applied mathematical preparation, information technologies, continuous education.

Прикладной    математической    подготовкой    (ПМП)    бакалавров технологического направления [2] называется составляющая математической подготовки студентов второго года обучения, структуру и содержание которой определяет интегрированный комплекс прикладных глав математики и соответствующих информационно-компьютерных средств. Другими словами, под ПМП понимается математическая подготовка, содержание которой определяют прикладные главы математики и в процессе которой формируются умения применения математических методов для решения прикладных инженерных задач с использованием информационно-компьютерных технологий.

Недостатки в системе непрерывного математического образования «школа – технологический университет», связанные с необходимостью качественного приобретения знаний прикладных разделов школьного курса математики для их применения в решении профессиональных задач высшей школы, создали предпосылки для внедрения технологии прикладной математической подготовки в процесс обучения учащихся старших классов – будущих бакалавров технологического направления.

В этой связи математическая подготовка учащихся 10-11 классов, основанная на применении информационно-компьютерных технологий, рассматривается нами как ключевой компонент непрерывного математического образования «школа – вуз».

На первом курсе студентами изучаются общие разделы математики, включающие в себя необходимый объем конкретных математических понятий и методов, исполняющих роль проводника к последующим прикладным знаниям. Общие разделы математики (линейная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисления функций одной переменной, обыкновенные дифференциальные уравнения) являются основой формирования содержания прикладной математической подготовки.

Прикладные главы математики представлены модулями, включающими разделы дифференциального и интегрального исчисления функций нескольких переменных, векторного анализа, теории числовых и функциональных рядов, уравнений математической физики, теории вероятностей и математической статистики, дискретной математики и линейного программирования.

Организация дидактического процесса прикладной математической подготовки, включающей школьные и общие разделы математики, состоит в выполнении следующих этапов.

I этап. Использование программных средств в процессе обучения математике в школе

Первичное знакомство учащихся с основными возможностями информационных систем MathCAD и Excel зачастую проходит на курсах компьютерной грамотности, организуемых технологическим университетом на базе школы в рамках программы непрерывного образования. Дальнейшая работа учащихся с программными средствами осуществляется на факультативных и практических занятиях под руководством преподавателя вуза с использованием специально разработанных учебно-методических пособий [1].

В качестве наглядного примера рассмотрим задачу полного исследования и построения графика функции.

Постановка задачи. Дана функция y = f ( x ) . Требуется:

3) Полное таблице.

провести полное исследование функции (используя средства дифференциального исчисления);

подкрепить аналитическое исследование компьютерной реализацией и осуществить проверку полученных результатов;

построить график функции.

исследование функции проводится по схеме, представленной в сводной

Исследование функции одной переменной у=J'x 1

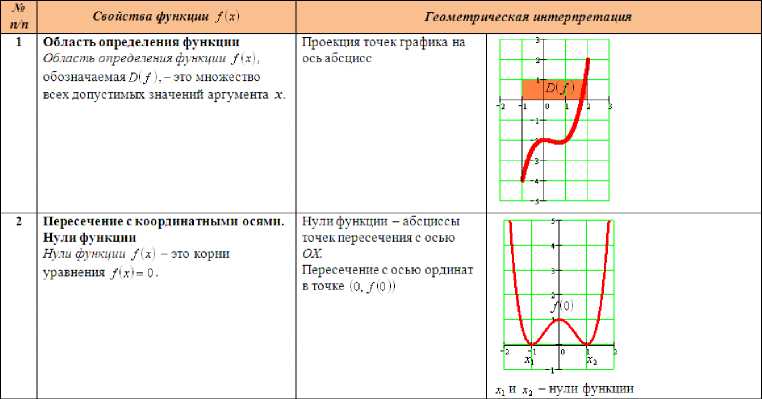
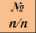
Свойства функции /(х)

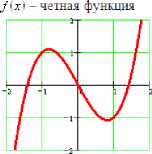
Четность (нечетность) функции Функция /(ж) называется четной, если для любого аргумента (Vx е Л(/ н выполняется равенство /• - х ¹ = / • х •, Функция /(х) называется нечетной, если для любого аргумента (Vx е D'/)) выполняется равенство /• - х • = -/• х •,

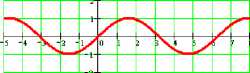
Периодичность функции

Функция /'xj называется периодической, если для любого аргумента ( Vx е D'/ и найдется положительное число Т (3 Г > Оi, называемое периодом функции, такое что

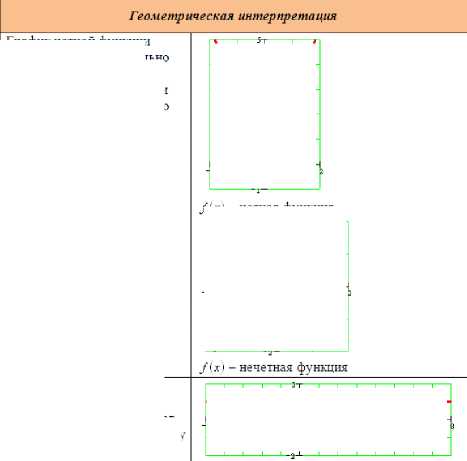
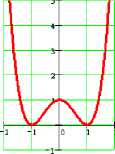
График четной функции симметричен относительно оси ординат.

График нечетной функции симметричен относительно начала координат.

График периодической функции состоит из повторяющихся фрагментов, длина которых равна периоду функции.

Свойства функции /(х)

Ограниченность функции

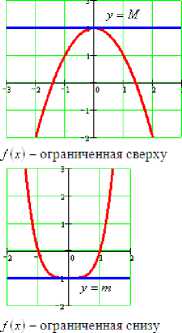
Функция /(х) называется ограниченной сверху, если Vx е D*/ • 3 М такое что /(х-< М.

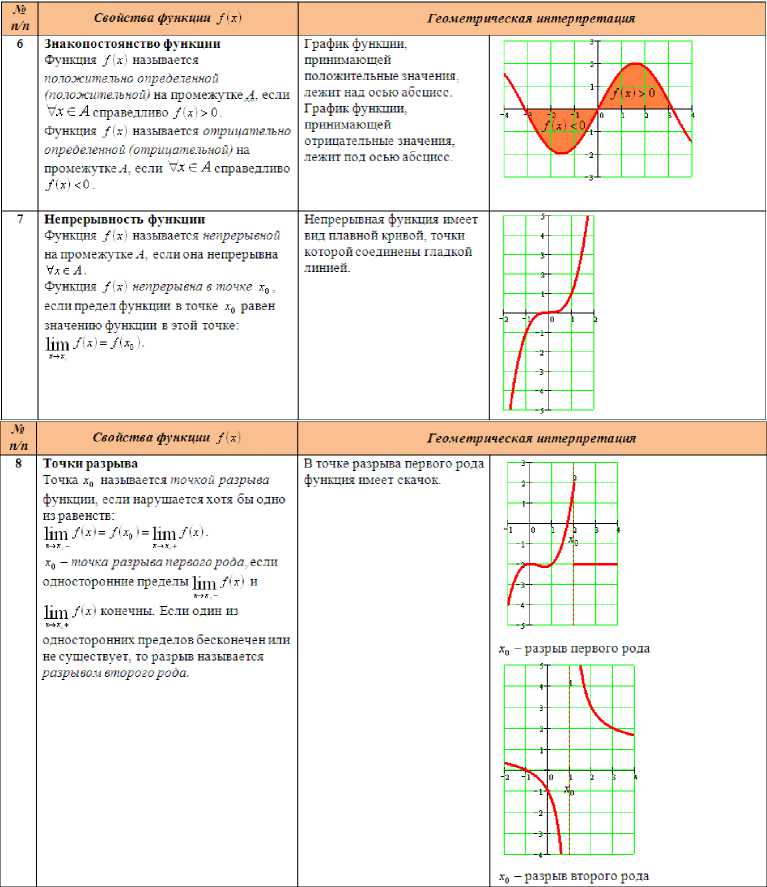
Функция /'xi называется ограниченной снизу, если VxeDi/ ¹ 3 т такое что /(х'> т.

Геометрическая интерпретация

График ограниченной сверху функции «не поднимается» выше прямой у = М.

График ограниченной снизу функции «не опускается» ниже прямой у = т.

Свойства функции JW*

Геометрическая интер пр стация

Свойства функции /(х)

Геометрическая интерпретация lint /• х। конечны. Если один из х0 - разрыв первого рода х0 - разрыв второго рода

В точке разрыва первого рода функция имеет скачок.

Непрерывная функция имеет вид плавной кривой, точки которой соединены гладкой линией.

односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода.

График функции, принимающей положительные значения, лежит над осью абсцисс. График функции, пр иним аю ще й отрицательные значения, лежит под осью абсцисс.

х₀ - точка разрыва первого рода, если односторонние пределы фц^ /• х • и

Непрерывность функции

Функция /(х) называется непрерывной на промежутке J. если она непрерывна Vxe^.                     " *

Функция /(х) непрерывна в точке х₀. если предел функции в точке х₀ равен значению функции в этой точке: 1ппУ ^ =У'^о

Точки разрыва

Точка х₀ называется точкой разрыва функции, если нарушается хотя бы одно из равенств: hm/'^'=/'^ ' = lim/w'-

Знакопостоянство функции

Функция /(х) называется положительно определенной (положительной) на промежутке^, если Vx € Л справедливо /-х- > 0.

Функция /'xi называется отрицательно определенной (отрицательной) на промежутке^. если Vx € Л справедливо

Свойства функции /(х)

Геометрическая интерпретация

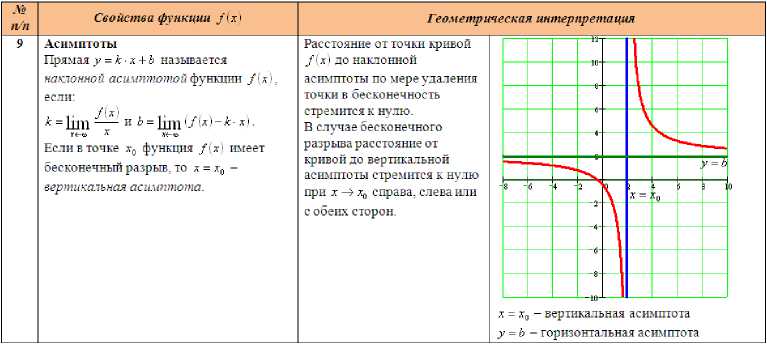
Асимптоты

Прямая у = к - х + b называется наклонной асимптотой функции /(х¹.

Расстояние от точки кривой /U¹ до наклонной асимптоты по мере удаления точки в бесконечность стремится к нулю.

В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты стремится к нулю при х -^ х₀ справа, слева или с обеих сторон.

х = х₀ - вертикальная асимптота у = Ь - горизонтальная асимптота

Если в точке х₀ функция /'х'\ имеет бесконечный разрыв, то х = х_п - вертикальная асимптота.

"= 11111 "-- 11 ^ = linr/'^'-£ л

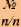
Свойства функции /М

С воиства функции j i х ■

Геометрическая интерпретация

Геометрииеская интерпретация

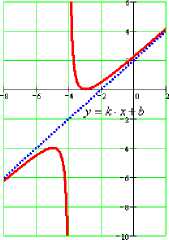
Монотонность функции

Функция /¹ х) возрастает на промежутке Л, если V х_рх₂ е Л таких что Xj < х₂ выполняется /’^'ъ’.

Функция /1 х) убывает на промежутке выполняется /■ ^ 1 > / (х21.

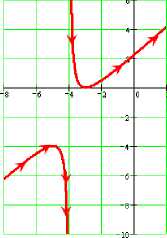
Признак монотонности функции

Функция /'xi возрастает (убывает) на промежутке Л. если УхеЛ справедливо

С увеличением значений аргумента график возрастающей функции «поднимается» вверх, убывающей - «опускается»

Л»

Свойства функции /(х)

Гео.м етрич е с кая интерпретация

Точки экстремума

Точки экстремума функции /(х i - это корни уравнения/'■ х • = 0. Точка, в которой функция меняется с возрастающей на убывающую называется точкой максимума, с убывающей на возрастающую - точкой минимума.

В точке максимума график функции имеет вид «горы», в точке минимума -«впадины».

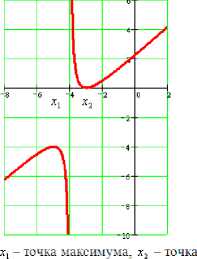
минимума

Свойства функции /(xi

Выпуклость функции

Функция /(х) выпукла на промежутке А.

Признак выпуклости функции

Если /"(х) > 0. то функция /(х i выпукла вниз. При   х¹< 0 функция /и¹

выпукла вверх.

Геометрическая интерпретация

График выпуклой вверх функции лежит не выше касательной, выпуклой вниз - не ниже касательной, проведенной к нему в любой его точке.

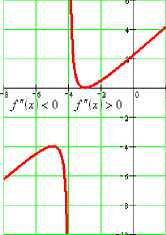
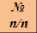
Свойства функция JU^

Точки перегиба

Точка х₀ называется /почкой перегиба функции /'ху если при переходе через неё функция меняет направление выпуклости. Точки перегиба функции / (х¹ - это корни уравнения /"' х¹ = 0 .

График функции переходит одной стороны касательной, проведенной в точке ■х0, /■ х0 н, на другую сторону.

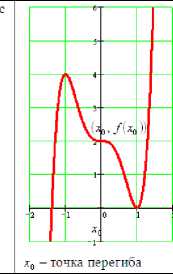
Свойства функции /(х)

Геом етрнческая интерпретация

Экстремальное значение функции Наибольшее значение функции /иг) на промежутке J - максимальное значение, принимаемое функцией на этом промежутке.

Наименьшее значение функции J-x- на промежутке Л - минимальное значение, принимаемое функцией на этом промежутке.

Наибольшее значение -ордината самой высокой точки графика, наименьшее -самой низкой точки.

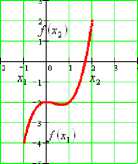
наибольшее значение

1Пш/(^,= /’Ч.) - наименьшее значение

Область значений функции

Область значений функции, обозначаемая Si/у-это множество всех значений, принимаемых функцией.

Проекция точек графика на ось ординат.

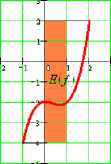
Свойства функции /(х)

Геом етрическая интерпретация

График функции

Графиком функции /'х' в выбранной системе координат называется множество всех точек и,^у для которых выполняется равенство у = /»хк

Чтобы кривая на декартовой координатной плоскости быта графиком функции, необходимо и достаточно, чтобы всякая прямая, параллельная оси ординат, пересекала её не более чем в од ной точке.

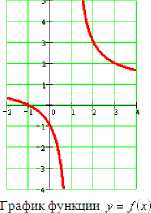
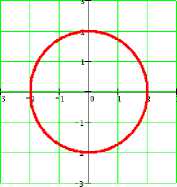
Не является графиком никакой функции, так как некоторым значениям аргумента л соответствуют два значения у.

II этап. Входной контроль – проверка базовых знаний за школьный курс

Входной контроль осуществляется в начале августа с целью проверки знаний по математике в объеме программы средней школы. Контрольное мероприятие проводится в тестовой форме и содержит задания среднего уровня сложности и позволяет преподавателю оценить полноту и устойчивость имеющихся математических знаний, выявить пробелы и актуализировать математические знания. Анализ полученных данных позволяет корректировать структуру и содержание нулевого семестра, тем самым устранять выявленные пробелы.

• III    этап. Нулевой семестр

Двухнедельный нулевой семестр организуется с середины августа для студентов, желающих улучшить качество знаний по математике. Содержание занятий в нулевом семестре формируется по данным первичного входного контроля, что позволяет оперативно устранить пробелы и подготовить студентов к аудиторной работе.

• IV    этап. Интегрированная лекция

Содержание общих курсов лекций определяет основное содержание и характер практических занятий и внеаудиторной работы. Наряду с систематическим курсом в преподавательской практике используются различные формы лекций: вводная (установочная) лекция, проблемная лекция, обобщающая (обзорная) лекция, лекция-конференция.

На вводных лекциях раскрываются основные возможности информационных систем MathCAD и Excel, не требующие наличия у студентов первоначальных знаний о технических возможностях и способах работы в системах. Дальнейшая самостоятельная работа студентов с информационными системами осуществляется на практических занятиях под руководством преподавателя-практика.

На классических (традиционных) лекциях возможности применения информационных систем демонстрируются при подкреплении теоретического материала решением задач. В качестве наглядного материала используются плакаты, иллюстрирующие теоретические сведения по теме.

Особое внимание применению информационных технологий уделено при проведении обобщающих (обзорных) лекций и лекций-конференций .

Обобщающие лекции систематизируют широкий круг знаний, полученных студентами в процессе изучения раздела, и являются основным методом изучения нескольких тем. На таких лекциях нами практикуется использование аудио- и видеоматериалов с лекциями профессоров МГУ (г.Москва) и СПГУ (г.Санкт-Петербург).

Лекции-конференции отводятся на проведение студенческих конференций, имеющих научно-практическое значение. Роль преподавателя состоит в том, чтобы корректировать подготовительную работу студентов, акцентировать внимание на главном в содержании, при необходимости выдвигать проблемные вопросы.

• V    этап. Комбинированное практическое занятие

В соответствии с календарным планом, лекции перемежаются с практическими занятиями (аудиторными, комбинированными, бинарными и лабораторными практикумами).

Аудиторное практическое занятие как самая распространенная разновидность практических занятий предполагает совместную работу преподавателя и студентов в оборудованной аудитории. Как правило, решение задач проводится «вручную» на доске с возможным применением наглядных пособий без привлечения информационных систем и программных средств.

Комбинированные практические занятия выполняют важную роль в повышении эффективности математической подготовки. В качестве оборудования аудитории для проведения комбинированного практического занятия используется ноутбук, проектор, экран или интерактивная мультимедийная доска. В отдельных случаях, соответствуя определенной дидактической цели, может быть задействован мобильный или компьютерный класс. На комбинированных практических занятиях помимо решения задач традиционным способом преподавателем раскрываются основные возможности программных средств в решении прикладных задач. Например, при полном исследовании функции средствами дифференциального исчисления можно не только осуществить контроль полученных аналитически результатов расчета, но и построить график функции, отличающийся высоким качеством изображения (рис. 1, 2).

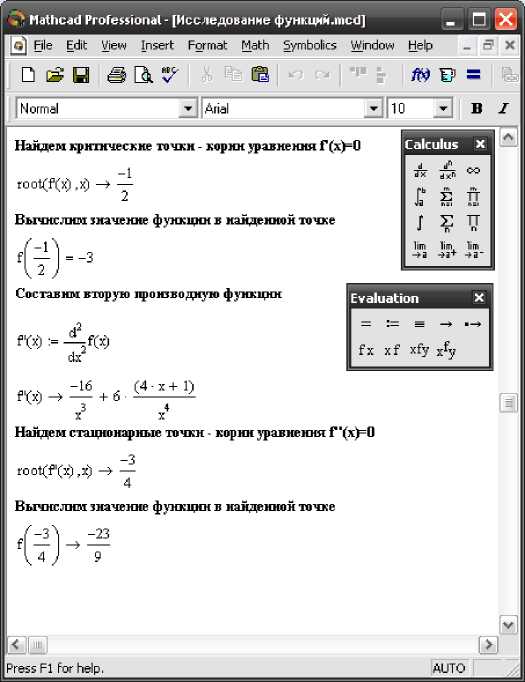
Рис. 1. Исследование функции с помощью MathCAD

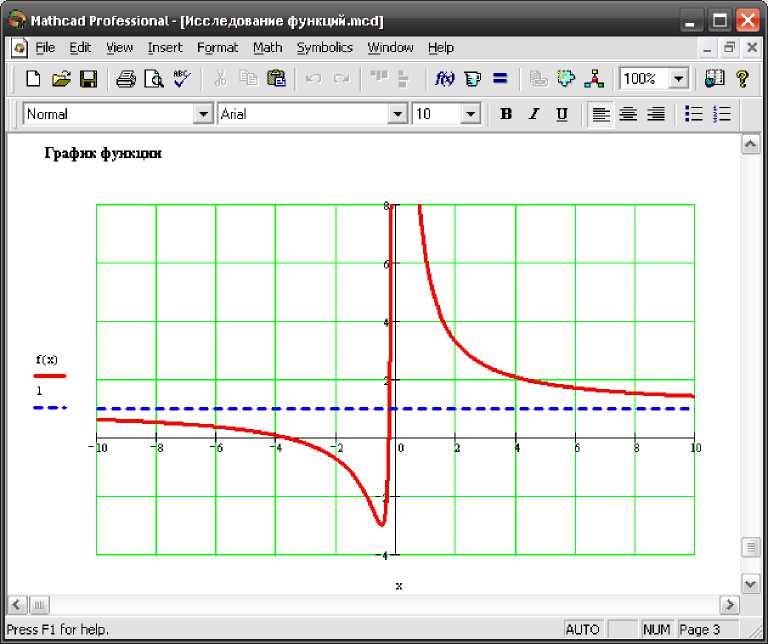
Рис. 2. Построение графика функции с помощью MathCAD

Лабораторный практикум – более высокая ступень лабораторных занятий. Лабораторные практикумы проводятся в мобильных и компьютерных классах, оборудованных современной техникой и соответствующим программным обеспечением. На таких занятиях студенты имеют дополнительную возможность экспериментировать с первоначальными данными, исследовать устойчивость полученных решений, оценивать результаты экспериментов. Во время выполнения лабораторного задания преподаватель выступает как консультант.

Бинарные практические занятия – новшество в преподавании дисциплины. Занятия проводятся на английском языке совместно с преподавателем иностранного языка. Подготовка к таким занятиям занимает довольно много времени не только у студентов, но и ведущих преподавателей, что вызывает значительные трудности. В качестве оборудования аудитории используется ноутбук, проектор, экран или интерактивная мультимедийная доска. Например, обзорная лекции по матричной алгебре была проведена нами в виде лекции-номинации «Matrix» . Ведущими конкурса выступали студенты, которые номинировали участников – различные виды матриц.

• VI    этап. СРС с помощью информационно-компьютерных технологий

Самостоятельной работе студентов (СРС), предусмотренной учебной программой, отведено особое место в структуре математической подготовки. Для обеспечения эффективности СРС обязательно должна осуществляться под руководством преподавателей и ими контролироваться. Для самостоятельной подготовки рекомендуются учебники, учебно-методическая и справочная литература.

• VII    этап. Контрольная работа с использованием тестовых технологий

Письменная аудиторная контрольная работа проводится по индивидуальным вариантам по завершении изучения каждого раздела. Вследствие недостатка времени, большинство контрольных работ предусмотрено в виде двухуровневых тестов закрытой формы (с выбором правильного ответа) и открытой формы (с записью ответа на бланке), включающих задания и знание теоретического материала.

Лабораторный (компьютерный) контроль знаний студентов по математике с использованием программных средств существенно меняет позицию преподавателя в учебном процессе. Лабораторный контроль носит массовый характер, поскольку его можно проводить на больших группах студентов. К тому же обработка результатов для получения окончательных оценок проводится легче и быстрее, чем проверка контрольных работ.

В качестве дополнительного средства контроля нами периодически проводится тестирование студентов в режиме off-line по контрольно-измерительным материалам, представленным в рамках федерального интернет-тестирования (, .

• VIII    этап. Экзамен с интеграцией теоретической и практической частей

В состав экзамена входят практическая и теоретическая части. Началом экзамена является предварительная проверка качества знаний в форме математического диктанта, состоящего из 10-15 вопросов теоретического и практического характера. Во время проведения диктанта преподавателем четко формулируется вопрос (задание), на обдумывание и запись ответа к которому отводится не более 1-3 мин. Прохождение проверки (выполнение не менее 50%) гарантирует допуск студента к основной части экзамена, в противном случае попытка сдать экзамен повторно откладывается на период дополнительной сессии.

Как правило, теоретическая часть включает в себя раскрытие основных положений одной из рассмотренных тем, практическая часть предусматривает решение двух-трех задач, степень выполнения которых дифференцирует оценку на экзамене. Итоговый результат по курсу математики (экзаменационная оценка) учитывает не только результаты входного, текущего контроля и самостоятельной работы, но также активность участия и регулярность посещения занятий.

Прикладная математическая подготовка была эффективно обоснована в ходе педагогического эксперимента на базе Волжского филиала Казанского государственного технологического университета и Волжского городского лицея (СОШ №7).