Динамические модели природно-техногенных рисков

Сложное сочетание факторов природного и техногенного характера, вследствие которых возникает угроза здоровью и жизни населения, проживающего на определенных территориях, а также материальным ценностям и объектам, в том числе критически важным, определяет исследования природно-техногенных рисков, которым посвящен целый ряд современных работ [8; 9; 10; 14], включая научные работы по математическому моделированию рисков [5; 11; 13].

Для обеспечения безопасности населения и территорий от проявления опасных природно-техногенных процессов в России ориентируются на стратегии, указанные в государственной научно-технической программе «Безопасность населения и народнохозяйственных объектов с учетом риска возникновения природных и техногенных катастроф» [4]:

• 1)    предотвращение причин природно-техногенных аварий и катастроф и обеспечение регламентного функционирования объектов, отличающихся техногенно опасными факторами;

• 2)    предотвращение и локализация опасной обстановки, из-за которой начинается цепная реакция событий, ведущих к природно-техногенной аварии или катастрофе;

• 3)    максимально возможная нейтрализация и оперативная ликвидация воздействий опасных природно-техногенных факторов на людей и окружающую среду.

Необходимо при этом учитывать, что экстремальные события, реализация которых маловероятна с точки зрения статистики, отражают «хвостовые» значения генеральной совокупности и, как правило, недооцениваются исследователями. Однако последствия таких событий весьма грандиозны и опасны (землетрясения, сильные наводнения, суперпожары, селевые катастрофы и др.) [2].

Одним из важнейших методов оценки природных и техногенных рисков в природно-технических системах (ПТС) является метод математического моделирования [12].

В настоящей статье представлены динамические модели природно-техногенного риска.

Результаты моделирования рисков при функционально подобных природных и техногенных воздействиях

Предположим, что риск представляет собой двумерную вектор-функцию, где r ₁( t ) – функция изменения природного риска, r ₂( t ) – функция изменения техногенного риска. Представим риск-функцию в виде системы дифференциальных уравнений [3]:

r'(t ) = a i r i ( t ) + b i r 2 ( t ) + L i (t), rl ⁽ t) = a 2 r i⁽ t ) + b 2 r 2 ⁽ t ) + L 2 ⁽ t ),

где a ₁, a ₂, b ₁, b ₂ – постоянные коэффициенты, отражающие реакцию ПТС на воздействия опасных природных и техногенных факторов; L ₁( t ), L ₂( t ) – функции, описывающие со-

Минаев В.А. и др. Динамические модели природно-техногенных рисков 5

ответственно интенсивность воздействия на ПТС внешних природных и техногенных факторов.

Общее решение системы (1) при нулевых функциях L1(t), L2(t) для случая положитель- ного дискриминанта ее характеристического уравнения записывается в виде ' r1( t) = C 1 e X1 t + C 2 e x2 t,

• r, ( t ) , ( ^ 1 2 ^ 1 ) c x . ■ + 1 ^ 1 2 2 1 1 c X 2 ■ . ^{2 b} 1 ^{1 b} 1 ²

Рассмотрим пример применения модели (1) для оценки природно-техногенного риска в случае, когда на ПТС оказываются функционально подобные внешние природные и техногенные воздействия. Под функционально подобным внешним воздействием понимается такой его вид, при котором влияния как со стороны природных, так и со стороны техногенных факторов описываются одинаковыми функциональными зависимостями.

Для начала используем функциональные зависимости линейного вида:

L⁰⁾( t ) = ^ 1 -П 1 1,

L^( t) = ^2 -П1, где ξ1, ξ2, η1, η2 – некоторые постоянные коэффициенты.

Найдем общий вид частного решения для неоднородной системы уравнений вида (1).

Представим систему (2) в следующем виде [1]:

' r . ( t ) = C 1 F_u( t ) + C 2 F j t ),

\ri( t) = C1 Fi.( t) + C 2 Fn( t), полагая при этом

' F _n( t ) = e ^Л1 t ;                 F .i ( t ) = e ^{X 1} t ;

' f „( t ) - ⁽ ^ ¹^ ^{; i i} e ¹¹ ' ; F 11 ( t ) "■■J" e ¹² ' .

[                  ^ 1                                 b 1

Запишем (4) в матричной форме:

< Г 1 ( t ) AJ F 11 ( t )   F 11 ( t )V C 1 )

Iri(t)J "IF11(t)  Fii(t)ЛC2J, или более компактно:

R0(t) = F(t)C0, где R0(t) – матрица функций изменения компонент природно-техногенного риска без учета внешних воздействий системы (4); F(t) – матрица системы (5); C0 – матрица коэффициентов системы (4).

В этом случае частное решение системы (1), соответствующее нахождению матрицы R ( t ) функций изменения природно-техногенного риска вследствие влияния на ПТС внешних воздействий со стороны природной среды и техносферы, будем искать на основании следующего соотношения [6; 7]:

R i ( t ) = F ( t ) J F ^{- 1}( t ) L( t )dt,                                (7)

где F ^–1( t ) – матрица, обратная матрице F ( t ); L ( t ) – матрица изменений внешних природно-техногенных воздействий на ПТС.

6   в ыпуск 2/2020

Построим матрицу F ^–1( t ), для этого найдем определитель матрицы F ( t ):

F 11 ( t )

F 21 ( t )

F 12 ( t )

F 22 ( t )

= Fn( t) F22 (t) - F21 (t) F12 (t) = (X 2  X1) e (^2))

b1

Матрица алгебраических дополнений F(t) для матрицы F(t) будет иметь следующий вид:

F ( t ) =

(^ 2 ai)

bi xtt

< ^- e 2

e

. ^2 1

-

e

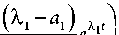
b ₁

. ^1

.

Тогда матрица, транспонированная по отношению к матрице (9), записывается как

F^T ( t )

4^X 2 ^- a i ) e ,2 t b i

(X1 — ai ).Xit e

(      bi

-e

, ^X 2 1

e "ⁱ t

Определим с учетом (10) подынтегральную функциональную матрицу U ( t ):

U ( t ) = F "4 1 ) L ( t ) = 4 A

'(X 2- ai) e ^21 bi

(^i- ai )^i t --e

V      bi

-e

, ^X 2 1

X] t e1t

< L i ( t ) ) V L 2 ( t ) J .

Рассмотрим функционально подобное воздействие на ПТС вида (3). На рисунке 1 показаны величины подобного воздействия на ПТС со стороны природной среды и техносферы в условных единицах, по оси абсцисс указано характеристическое время. Такие виды воздействий описывают проявления подвижек, возникающих в геологической среде и приводящих к возникновению катастрофических сейсмических событий, наблюдаемых на территориях районного, локального и точечного масштабного уровней. Они характеризуются внезапными аварийными ситуациями на объектах техносферы, например, взрывами оборудования, обрушениями зданий, сооружений, конструкций различного вида.

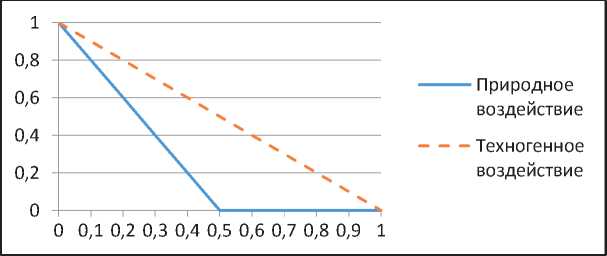
Рис. 1. Природно-техногенное подобное воздействие на ПТС вида (3)

Минаев В.А. и др. Динамические модели природно-техногенных рисков

В этом случае матрица изменений внешних природно-техногенных воздействий на

ПТС имеет вид

L (t) = ( L(0)( t)) =

[ L-( t ч [ L*( t ))

‘

-K* Tt)^2-n2 tJ

■ П1n

.

Определим компоненты матрицы U ( t ):

b1

u ^{1 (} t) ( X ₂ -X1 ) e ^(x^^x2^ t

(^X 2 ^- a l )

b ₁

e ^X 2 tL( t ) - e ^X 2 t L ₂( t ) =

_[ ( X 2 - a i ) L 1 ( t ) - b l L 2 ( t ) ] e "^1 t

X 2-X1

По аналогии получим выражение для u ₂( t ):

.

u 2⁽ t ) =

[b1 L2(t) -(X1 -

^ 2 -

al) L1(t)]e ■ ^1

,^-^ 2 t

.

Проинтегрировав выражения (13)–(14), получим следующие функции:

X 1^{( 1} ) = J u i ^{( 1 ) d1} =

[—Ь1П2 +(X 2— a 1 )П1 ] e—

S

% 2^{( 1} ) = J u 2^{( 1} ) ^dt =

^1 (^ 2 —^1)

• X1 1

^

—+ c_p

-

ai )П1 + И,- ] e

—

X2 (X2-^1)

■ ^2 1

^

—+ ( 2 2 ,

где C ₁, C ₂ – постоянные коэффициенты, учитывающие изменения природных и техногенных воздействий на ПТС в начальный момент времени.

Учитывая (15), раскроем соотношение (7):

j ^ ( t ) = F ( t ) x (t ) =

' F i ( t ) F j t ) )f X i ( t ) ' F 21⁽ t ) F 22⁽ t ) % 2^{( t} ) "

7

\     7

После ряда преобразований в итоге получим выражения для функций изменения природного и техногенного риска в ПТС:

r 1⁽ t ) = D i e ^X 1 t + D 2 e ^X 2 t + T¹- [ ( ^ 1 +^ 2 ^- a 1 ) П 1 ^{- Ь}1 П 2 ] , Л 1 Л 2

r,( t) .f^L-all D1 e >- + b1

(X 2 - a

b1

)                1

—D^e +--1 a.b,П1+(^ — a^ )(^2 -a

2                      11  2       1     1     2

^b 1 X 1 X 2

~

~

где D1 = C 1 + C 1; D2 = C2 + C2.

Рассмотрим на рисунке 2) подобное воздействие со стороны природных и техногенных факторов вида

L(i0)( t) = ^i -4it 2, L(20)(t) = ^2 -П2t2.

8   в ыпуск 2/2020

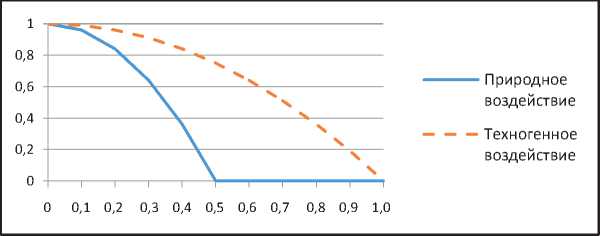
Рис. 2. Природно-техногенное подобное воздействие на ПТС вида (18)

Воздействия такого вида (параболического), например со стороны геологической среды, характеризуют воздействия геодинамических опасностей, интенсивность которых плавно уменьшается с расстоянием от эпицентра их проявления. К таким опасностям относятся криповые, карстово-деформационные, просадочные, оползневые процессы, охватывающие территории локального, районного и регионального масштабного уровней. В отношении техносферы в качестве примеров можно привести пожары, выброс химических веществ, выпадение радиоактивных осадков.

Найдем матрицу изменений внешних природно-техногенных воздействий на ПТС:

L (t) = ( L(0)( t))

[ L-( t >1 t L?( t )J

‘ p 1 -n1t21 (5.-n. t2)

—2n1 t

-2n2 t

или

L 1 ( t ) = — 2 ^ 1, L 2 ( t ) = —2 П 2 1 •

Будем искать частное решение системы (1) для случая (18) методом вариации произвольной постоянной. Для этой цели представим систему (2) следующим образом:

' r ( t ) = C i ( t )e ^{X l} t + C 2 ( t )e ^X 2 t ,

,         , (X. — a,) ,           (X2 — a.) ) ,

Г 2 ( t ) = C 1 ( t Г 1, ^U e ^{X l} t + C 2 ( t Г 2, ^U e ^X 2 t .

[                       bi

Продифференцируем уравнения системы (20):

• dr ^ ^t) = C ‘ ( t )e ^^l t + C j ( t ) X e . ^^l t + C ‘ ( t )e ^x 2 t + C ₂ ( t ) X ee ^x 2 t ,              (20.l)

dt 1       11     2        22

zJ^,"a,)        zx^(^i-a,)

r 2 (t)2 = C ‘( t )LJ---^l . "^l t + C ( t )^^---^l e "^l t +

dt 1b11b1

+ C‘ (t)(X2 " al) e"2t + C2 (t)X2 (X2" al) e"2t.                    (20.2)

2 _{b 1} 2 _{b 1}

	Минаев В.А. и др. Динамические модели природно-техногенных рисков 9
С друго	й стороны, согласно системе (20) имеем dr^t) = a^ ( t ) e X 1 t + a C ( t ) e '2 t + b I^ lZ a ) q ( t ) e X 1 t + 1 1                  1 2                   1                      1 dt                                            b 1 +    b 1 ( ,     ) c 2( t ) e 2 + L1 ( t ),                            (21.1) b 1 dr2^ = a 2 C i ( t ) e X i t + a 2 C 2 (t ) e t + b 2 ( ^l^ a i ) C i (t ) e ^ + dt                                             b 1 +    ь ( ^ 2 - a i ) C ( t)emt + l ( t ).                          (21.2) 2       b i          2                2
Прирав соответств	нивая правые части выражений (20.1) и (21.1), выполняя группировку и делая ующие преобразования, получим C ‘ ( t ) e " 1 t + C 2 ( t ) e " 2 t = L 1 ( t ).                             (22)
Продел	вая схожие действия с выражениями (20.2) и (21.2), запишем C ‘ ( t ) ^ - a 1 ^ e "1 t + C 2 ( t ) ( X2" a 1 ^ e X 2 t = L 2 (t ).                  (23) b 1 b 1
В итоге	получаем следующую систему: ' C ‘ ( t ) e X 1 t + C 2 ( t ) e ^2 t = L 1 ( t ), * />.(^1— a i )          /Л^г— a i )                                (24) C 1 ( t Г 1, U e X l t + C 2 ( t Г 2, U e ^2 t = L 2 ( t ). [              b 1                           b 1
Произв	дя интегрирование (24), получим окончательные выражения для функций
C 1( t ) и C 2(	t ): c ( t ) = г [ b 1 L 2( t ) - ( ^ 2 - a 1 ) L 1( t ) ] e "1 tdt , < 1     J               Х 1 -X 2                                    (25) C 2 ( t ) = J [ L 1 ( t ) e -X 2 t - C ‘ ( t ) e (X 1 -X 2 ) t ] dt .
Подстав	ляя в (25) выражения (19) и осуществляя интегрирование, найдем 2 [^ 2 b1 —п 1 ( ^ 2 — a 1      + ^ 1 t ) -XYt C 1( t ) =         X 2 ( X , -X 2 )          e    + C 1’                 (26) cm- ZDl iI ^ iZ a il zn i b iJ Ii+^l t l „-^ 2 t +c C 2( t ) =          x 2 ( x 1 -x 2 )          e    + C 2,                 (27)
где C 1 и C генных воз	2 – постоянные коэффициенты, учитывающие изменения природных и технодействий на ПТС в начальный момент времени.

Выпуск 2/2020

Окончательно получаем

2     Г ( п b i -П 1 ( X ₂ - a 1 ) ) ( 1 + X 1 t ) [n , ( ^ - a 1 ) -q ₂ b ] ( 1 +X 2 t )

r t ) = ( X 1 -x 2 ) [             X 2              +             X 2

+ D 1 e X 1 tt + D 2 e X 2 ,
r ( -1 - ж-4	( X 1 - a 1 ) [ n 2 b 1 — n 1 ( X 2 - a 1 ) ]( 1 + X 1 t ) + (X 1 - a 1 ) [Л 1 ( X 1 - a 1 ) -n 2 b 1 ]( 1 + X 2 t ) .                  X 2                                         X 2	(2 8) + 1

J^X a ^{! X} 1 _e + (X2 a ¹ ) ^X 2

.        b 1          ¹                b 1          ²

_ — ~ ~

где D1 = C 1 + C 1; D2 = C2 + C 2.

Итак, выше обоснованы и реализованы две новые математические модели оценки природно-техногенного риска, возникающего в природно-технических системах под влиянием функционально подобных воздействий, то есть воздействий со стороны природных и техногенных факторов, описываемых функциональными зависимостями одного вида. Первая модель характеризуется линейным видом воздействий и описывает проявления подвижек, возникающих в геологической среде и приводящих к возникновению катастрофических сейсмических событий. Подобные виды воздействий характеризуются внезапными аварийными ситуациями на объектах техносферы, например, взрывами оборудования, обрушениями зданий, сооружений, различных конструкций. Вторая модель описывает воздействия параболического вида, интенсивность которых плавно уменьшается с расстоянием от эпицентра их проявления. Они описывают криповые, карстово-деформационные, просадочные, оползневые процессы.

Развивая динамическую модель природных и техногенных рисков, описываемую дифференциальными уравнениями (1), далее разрешим их для случаев, когда на природно-техническую систему оказываются функционально различные природные и техногенные воздействия.

Результаты моделирования рисков при функционально различных природных и техногенных воздействиях

Случай 1. Пусть техногенные воздействия отражают проявления подвижек, возникающих в геологической среде и приводящих к возникновению катастрофических сейсмических событий на территориях. Подобные виды воздействий показаны на рисунке 3 в виде второго уравнения (29) для L 20 ⁰ ( t ) .

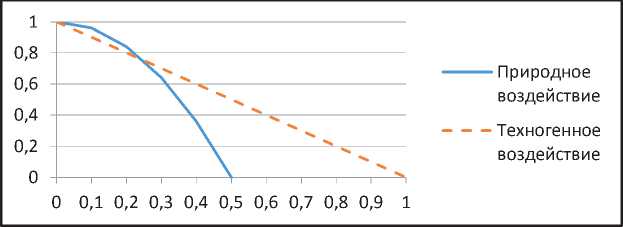
Рис. 3. Природно-техногенное функционально различающееся воздействие вида (29) на ПТС

Минаев В.А. и др. Динамические модели природно-техногенных рисков 11

В то же время природные воздействия описываются уравнением параболического вида (первое уравнение в (29) для Д ⁰ ) ( t ) ), интенсивность которых плавно уменьшается с расстоянием от эпицентра их проявления, отражая так называемые медленные катастрофы – криповые, карстово-деформационные, просадочные, оползневые процессы:

L^LyX t ) = ^ 1 -П 1 12,

Lnt) = ^2 -П2t, где ξ1 , ξ2 , η1 , η2 – некоторые постоянные коэффициенты.

Матрица изменений внешних природно-техногенных воздействий на ПТС для (29)

имеет вид

L ( t ) = ( L ^(o)( t ) ) =

f Ln t ) ) [ L⁽?( t ) J

‘- pil -Я1 t) [52 -n, t J

^{- 2 n} 1 t

П , J ,

или

L 1 ( t ) = - 2 ^ t, ^L 2⁽ t ) = -^П 2 -

Применяя процедуру, описанную выше, определим C ₁( t ) и C ₂( t ) как частные решения системы (30) для случая внешних природно-техногенных воздействий на ПТС вида (29) (см. рис. 3).

Для C ₁( t ) и C ₂( t ) имеем

C 1⁽ t ) - ^-

Х2 (х -X 2)

[ ² П 1 (^X 2 ^- a 1 )( ^{1 + X} 1 t ) - ^Ь 1 П 2 ^Х 1 ] ^e

^^^^в

■^X1 t + C 1 ,

C 2 ( t ) =

[ 2 П 1 ( Х 1 ^- a 1 )( ¹ + ^ 2 t )^- b ^2 X 2 ] e

^^^^в

^X 2 ^(X 1 -^Х 2 )

• ^X2 t

---⁺ C 2 ,

где C ₁ , C ₂ – произвольные постоянные интегрирования; λ ₁, λ ₂ – корни однородного характеристического уравнения для (1).

Тогда соотношения для функций изменения природно-техногенного риска для ПТС, в случае совместного функционально различающегося воздействия вида (29) со стороны природной среды и техносферы, в итоге примут следующий вид:

' r( t ) = D₁ e ^¹ t + D 2 e '² t + V^ t ),

у ( t ) = ^{( X 1}   a ¹ ) De ^¹ t + ^{( X 2}   a ¹ ) De ^2 t + v ( ⁽³⁾( t ),

2      1      22

b ₁ b ₁

где D ₁, D ₂ – постоянные коэффициенты, учитывающие изменения природных и техногенных воздействий на ПТС в начальный момент времени, а функции V ₁⁽³⁾( t ) и V ₂⁽³⁾( t ) определяются уравнениями

<

_{v (}3) , t ) = b i H 2 ^ i ^— 2 ^ 1 ( X 2 ^— a i )( ¹ + X i t ) + 2 П 1 ( Х ₁- й 1 )( 1 + Х 2 е ) - Ь 1 П 2 Х ₁

1                X2 (Х1—X2)                    x 2 (X1—x 2)         ,                  (35)

_V (3) ( t ) = (^X 1 ^{— a} 1 ) [ b 1 H 2 ^X 1 ^{— 2} П 1 (^X 2 ^{— a} 1 )( ^{1 + X} 1 t ) ] + (^X 2 ^— a 1 ) [ ² П 1 (^X 1 ^— a 1 )( ^{1 + X} 2 t ) ^{— Ь} 1 П 2 ^Х 2 ] 2^U                b 1 X 2 ( X 1 —x 2 )             ⁺              b 1 X 2 ( X 1 —X 2 )

—

—

—

—

.

12 в ыпуск 2/2020

Случай 2. Рассмотрим на рисунке 4 функционально различающиеся воздействия вида.

L(i0)( t) = ^i -П12,

L^( t ) =

^2 + Пt "

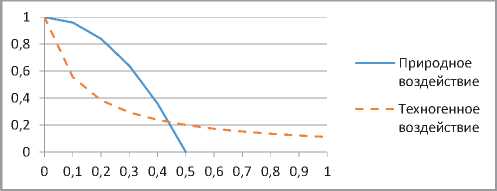
Рис. 4. Природно-техногенное функционально различающееся воздействие вида (36) на ПТС

Из рисунка 4 следует, что природное воздействие описывается уравнением параболического вида. Первое уравнение в (36), интенсивность которого плавно уменьшается с расстоянием от эпицентра его проявления, в то время как интенсивность техногенного воздействия (второе уравнение в (36)), снижается с течением времени. Матрица изменений внешних природно-техногенных воздействий на ПТС имеет вид

L (t) = ( L(0)( t))

f ^L-⁽ t > 1

V L0( t )j

P‘-n, t2)V ?2 +П2t >

f -2П, t )

П2

V (?2 +П2t)2 ,

или

L( t) = ^

L 2 ( t ) =

П 2

(^2 +П2 t )2

Найдем частные решения C ₁( t ) и C ₂( t ) системы (2) для случая внешних природно-техногенных воздействий на ПТС вида (36), также используя вышеприведенные результаты:

1                                                                      Л 1 1

C 1 ( t ) =

^--^- 12ч, (X,— a 1 )f te -l1 dt— k.42 J(^+nt)2 dt'.

Анализируя (39), видим, что взятие первого интеграла не составляет особого труда, однако второй относится к классу «неберущихся».

Для его приближенного нахождения разложим подынтегральную функцию

f (t)=

—Xit e 1t

(^2 +П2 t )2

в степенной ряд в окрестности точки t = t ₀.

Минаев В.А. и др. Динамические модели природно-техногенных рисков 13

Для этой цели найдем последовательно производные от функции (40). Производная первого порядка от функции (40) имеет следующий вид:

₍    _ [^1 ( ^ 2 ⁺ⁿ 2 1 ^{) + 2 n} 2 ) e ¹

f ^{( 1} )                           \3

(^2 +П21)

Найдем производную от функции (40) второго порядка:

f4t ) =

[ ^X2 ( ^ 2 +n t ) 2 + 4 X 1 ^ 2 ( ^ 2 +П 2 1 ) + 6П 2 ) e ""1 ¹

(^2 + П1 )4

.

Тогда производная третьего порядка будет определяться соотношением f'"(1)=-

[X3 (^2 + П1)3 + 6X2n (^2 + П1)2 + 18X^2 (^2 +П21)+ 24n2)e X11

(^2 + П1 )5

Выполняя дальнейшее дифференцирование функции (40) по переменной t , придем к следующему рекуррентному соотношению:

( - 1)

f ⁽ n ) ( t ) =

xn (^ + П21) n + fm xn - m+1nm—1 (^ + П21) n - m+1 n (n - k)+(n + 1)!n 2

.                        m = 2                                           k = 0

(^ 2 +П21) n+2

—Xi 1

e ^{1 t}

. (44)

Учитывая (44), функцию (40) представим в окрестности точки t ₀ в виде ряда, разложенного по степеням ( t - t ₀):

f ⁽ t ) = f ^{( t} o ) ⁺ f'^{( t} oXt ^{- t} o ) ⁺    2^ ⁽ t ^{- t o ) 2 +}

'"((

+ fTT02 (t-to)3 + - + ^Ч"02 (t-to) n + -

3!

Степенной ряд (45) сходится как в окрестности точки t ₀, так и во всех точках интервала [0; 1], являющегося модельным интервалом изменения переменной t .

Численные оценки, выполненные авторами, показали, что необходимая точность расчетов 0,001% достигается при учете первых семи членов ряда (45). Вводя обозначения W o = f ^{( 1} o ); W 1 = f ^{, ( 1} o^)/1! ; W 2 = f "^{( 1} o^)/2! ; -; W 6 = f ^{(6) ( 1} o^)/6! , запишем функцию (40) в следующем виде:

—^11

f (1) = 4    2 = Z Wn (1 — 1 o) n / n!.(46)

(^2 +П21)

Тогда второй интеграл выражения (39) представляется в виде

, e 1^d1_v = f]L W n ( 1 - 1 o ) n / n ! d1 = J[ W ) + W 1 ( 1 - 1 o )/1! + W 2 ( 1 - 1 o ) 2 /2! + W _; ( 1 - 1 o )³/3! +

(^2 +П21)    Jn=o

+ W 4 ( 1 - 1 o )⁴ /4! + W 5 ( 1 - 1 o ) 5 /5! + W 6 ( 1 - 1 o )⁶ /6!] d1 = W o 1 + W ¹⁽^ - ^{1 o)} + W 2 ⁽ - - ^{1 o)} +

+ W 3 ( 1 - 1 o )⁴ + W 4 ( 1 - 1 o )⁵ + W 5 ( 1 - 1 o )⁶ + W 6 ( 1 - 1 o ) 7

6, W„ ( 1 - 1 ₀) p ^{+ 1}

+ C o = ^W o 1 + E p   o— + C o .

p = 1    ⁽ p ^{+ 1)!}

14 в ыпуск 2/2020

Итак,

e ’"1 t dt         4   V W p ( t - 1 0 ) p ⁺1    c

— Wot +                 + Co.

J(^2 +П21 )2          ^^1   (P + 1)!

Находя первый интеграл из выражения (39) и последовательно преобразовывая это выражение, получим окончательное соотношение для функции C ( t ):

c 1⁽ t ) -^—

1 Г 2 П 1 ( х 2

—

X1 —X 2

- a1 )(1 + X1 t) —х11

X 2            ^e

^

+ ^2 ^{Х (} t ) ^{+ C} 1 ,

где C i - произвольная постоянная интегрирования, а функция Х ( t ) определяется выражением

6 W ( t - 1 ) p ^{+ 1} X ( t ) = W_ot +    4 —0—

.

⁰     ^^ 1 ( p + 1)!

Найдем производную от функции C ₁( t ):

C ‘(t) = — V

Xi

^^^^^^в

— [2 ni (X 2 — ai) te "^ t

Л 2

—

^2^Ф ( t ) ] ,

где функция Φ ( t ) определяется выражением

Ф( t) = E Wq (t - 10) q , q=0

а коэффициенты W_q имеют тот же смысл, что и коэффициенты разложения в (45). Определим, как показано выше, функцию C ₂( t ):

C 2( t) = J1-2n1te-

,—X 2 1 _— [2 ^ 1 ( X 2 — ^a 1 ) te ^{—X 1} t —

-

X1 —X2

b , П,ф ( t )] e ^{( X 1 —X 2 ) t} ,

^{1 12 v 7J} ----------^ dt =

-

2nA

-

X1—X 2

a¹) J te ^—X 2 t dt +

Ml

X1 —X 2

J ф ( t ) e^{( X}1 ""^‘ dt =

2n1(X1— a1) I , , 1=             t + e

X 2(X1 —X 2) ( X 2 >

—

X 2 1 + ^Ь 1 П 2

X1—X

- Ф( t )

" 2 _

e ^{( X} i ^—X 2 ) t

-

X1 —X 2  X1 —X 2

J ф‘ ( t)e ^(X1-M t dt . (52)

Вычислим ненайденный интеграл в последнем выражении. Для этой цели введем обо- 6

значение Ф‘ ( t ) = У a W _a ( t — t ₀) ^{a 1} =^ ( t ), в итоге получаем

a= i

j T ( t )e^{(X 1} ' t dt =

e

, ^{( X} 1 ^-X 2 ) t 5

X1 -X 2

S G e ( t - t o ) ^e + C 0 , e= o

где <

G 0 = Wi —

G 1

G 3 = 4 W 4

X 1 —X 2’ 4 G 4

G1 = 2 W2 —

2G2

—

X1 —X 2;

G 4 = 5 W 5 —

X1 —X2 ;

30 W 6

X1—X 2;

G 2 = 3 W3

—

3G3

X1—X 2,

G 5 = 6 W 6 .

Минаев В.А. и др. Динамические модели природно-техногенных рисков

Окончательно функция C ( t ) записывается в виде

C (t) = 2П1(Х1 - a 1)(1 + X 21) _X21 +   b 2^2

ф ( t ) ¹— ^w X 1 -X ₂

A        X1X 2(X1 -X 2)   e      (X1 -X 2)2

где функции Φ ( t ) и Θ ( t ) определяются соотношениями

^{ф (} t) = 2 W q ⁽ t — t 0 ) q ;

q = o

5

0(t) = 2G.(t -1c)'- e=0

В конечном итоге функции изменения природно-техногенного риска в ПТС для случая совместного функционально различающегося воздействия вида (36) со стороны природной среды и техносферы представляются в виде

?( t) = D1 e X1 t + D 2 e 4 t + Q1( t )e X1 t + V^C t),

r ( t ) = ( Xr- a ¹) D X , t + ⁽ X ^{2 -} a , ) D X 2 t + _Q ( t ) e X _{l t} + V ⁽⁴⁾( t) 2                            1                              2              2                 2

bl                       bl где D1, D2 – постоянные коэффициенты; функции V1(4)(t) и V2(4)(t)определяются из уравнений

V⁽^(t t ) =

2 П 1

XA -x ₂)

(X1 - Й1)(1 + X 21)   (X 2 - a 1)(1 + X11)

x:                X,

V(4)( t ) =

2 П 1 b i X i ( X i -X 2 )

(X 2 - a1)(X1 - a 1)(1 + X 21) (X1 - a1)(X 2 - a 1)(1 + X11) —

X2                           X1

а функции Ω ₁( t ) и Ω 2 ( t ) – из уравнений

Qt( t) =

^Ь1 П 2

X , -X ₂

X1 -X 2

ф(t )-

X1 -X 2

0 ( t )

-X (t ) ^ ,

^ 2 ( t ) =

П2

X1 -X 2

^{( X} 2 ^- a l )

X1 -X 2

ф ( t )-r^ ⁰ ( t )

X1 - X 2

- ( X 1 - a 1 ) X ( t ) > .

Таким образом, неоднородная система уравнений (1), описывающая взаимосвязанную систему рисков природного и техногенного характера, на которую дополнительно накладываются влияния опасных функционально различающихся воздействий внешних природных и техногенных факторов, имеет понятные, хорошо интерпретируемые аналитические решения для ряда случаев. Представленные решения отличаются друга от друга видами воздействий: в первой модели рассматривается сочетание параболического (отражающего угрозы, интенсивность которых плавно уменьшается с расстоянием от эпицентра) и линейного (отражающего внезапно возникающие угрозы) воздействий; во второй модели – сочетание параболического и гиперболического (отражающего угрозы, интенсивность которых резко уменьшается с течением времени) видов воздействия.

16 в ыпуск 2/2020

Выводы

• 1.    В статье обоснованы и реализованы две новые математические модели динамики природно-техногенного риска, возникающего в природно-технических системах под влиянием функционально подобных воздействий, влияние которых на ПТС со стороны природных и техногенных факторов описывается функциональными зависимостями одного вида; а также две новые модели динамики природно-техногенного риска, возникающего в ПТС под влиянием функционально различающихся воздействий, влияние которых со стороны природных и техногенных факторов описываются разными функциональными зависимостями.

• 2.    Применительно к первому (подобному) типу воздействия относится первая модель, характеризующаяся линейным видом воздействий и описывающая проявления подвижек, возникающих в геологической среде и приводящих к возникновению катастрофических сейсмических событий. Подобные типы воздействий характеризуются внезапными аварийными ситуациями на объектах техносферы, например, взрывами оборудования, обрушениями зданий, сооружений, различных конструкций. Вторая модель подобного типа описывает воздействия параболического вида, интенсивность которых плавно уменьшается с расстоянием от эпицентра их проявления. Они описывают криповые, карстово-деформационные, просадочные, оползневые процессы.

• 3.    Представленные модели второго типа отличаются друга от друга видами воздействий. В третьей модели рассматриваются совместно параболический (отражающий угрозы, интенсивность которых плавно уменьшается с расстоянием от эпицентра) и линейный (отражающий внезапно возникающие угрозы) виды воздействий. В четвертой модели рассматривается параболический и гиперболический (отражающий угрозы, интенсивность которых резко уменьшается с течением времени) виды воздействий.

• 4.    Общий подход к моделированию природных и техногенных рисков, а также представленные решения направлены на использование в аналитической деятельности служб, осуществляющих предупредительную работу в связи с угрозами природного и техногенного характера, реагирующих на последствия реализовавшихся угроз. В основном это подразделения МЧС России, производящие анализ возникновения рисковых ситуаций и прогнозирование их развития. Рассмотренные модели легко адаптируемы к учету внешних природных и техногенных воздействий иного вида, например, экспоненциального или колебательного, нередко случающихся в реальной действительности. Кроме того, описанный теоретический подход к построению динамической модели может быть распространен на другие классы (типы) рисков, например антропогенных.

• 5.    На конкретном примере показано, что в случае сложных видов воздействий на ПТС, описываемых функционально «трудными» математическими соотношениями, можно применять их упрощенное представление в виде разложения в ряды и ограничиваться, в зависимости от требуемой точности расчетов, несколькими начальными членами ряда.

• 6.    Опыт моделирования показал, что математически можно достаточно точно описать практически любые виды сочетанного природно-техногенного воздействия на природно-технические системы. По результатам такого описания необходимо, на наш взгляд, составить специальный атлас комплексных воздействий на ПТС с целью превентивного

Минаев В.А. и др. Динамические модели природно-техногенных рисков 17 «проигрывания» различных ситуаций и выработки наиболее эффективного противодействия возникающим опасностям со стороны подразделений МЧС и других заинтересованных структур.