Длина волны электромагнитного поля в линиях электропередачи

Электроэнергетические системы представляют собой совокупность устройств для производства, преобразования, транспортировки и потребления электрической энергии.

Производство электрической энергии происходит на электростанциях различных типов. Преобразование электрической энергии обычно выполняется на трансформаторных подстанциях. Это преобразование чаще всего заключается в изменении класса напряжения с целью уменьшения потерь электрической энергии при ее передаче потребителю, который может находиться на значительном расстоянии от электростанции. Для передачи электрической энергии используют воздушные или кабельные линии электропередачи (ЛЭП).

Методика передачи электрической энергии на небольшие расстояния (до 200-300 км) достаточно хорошо разработана и изучена [1]. В ее основе лежит допущение о линейности распределения электрической энергии по токоведущим частям ЛЭП, а сама линия электропередачи принимается за линию с сосредоточенными параметрами. В принципе, это справедливо при передаче электрической энергии хорошего качества на небольшие расстояния.

Процесс передачи электрической энергии даже хорошего качества на большие расстояния (более 200-300 км) нельзя назвать линейным. Поэтому ЛЭП, участвующую в такой передаче, следует считать линией с распределенными параметрами [2]. При наличии в спектральном составе основных характеристиках передаваемой электрической энергии высших гармонических составляющих за линии с распределенными параметрами следует принимать и ЛЭП меньшей протяженности [3].

Качество электрической энергии в системах электроснабжения общего назначения в России регламентируется ГОСТ 32144-2013 [4], который допускает в определенных границах несимметрию, несинусоидальность, напряжение. Но эти границы нередко нарушаются, особенно в промышленных регионах страны. Поэтому современные ЛЭП даже небольшой протяженности во избежание погрешностей анализа результатов передачи электрической энергии следует принимать за линии с распределенными параметрами.

Электричество вполне можно считать одной из форм отражения действия электромагнитного поля на материальные объекты. В связи с этим передачу электрической энергии по токоведущим частям ЛЭП можно считать направленным распространением по ним электромагнитного поля.

При изготовлении токоведущих частей ЛЭП используют чаще всего алюминий, сталь, медь. Известно, что при малых значениях тока эти материалы обладают слабо выраженной нелинейностью, которая начинает заметно проявляться при перегрузках. Границы линейности установлены значениями допустимых токов, указанных в справочных материалах [1, 5]. Токоведущие части ЛЭП рекомендуется эксплуатировать в линейной области вольтампер-ных характеристик. Следовательно, неперегруженные ЛЭП линейны, а значит, при анализе результатов передачи по ним электрической энергии можно использовать принцип суперпозиций (анализ распространения каждой п -й гармонической составляющей, а также постоянной составляющей ( n = 0) напряжения и тока можно выполнять отдельно с последующим при необходимости обобщением результатов) [3].

Распространение электромагнитного поля в линейной среде происходит, как известно, по гармоническому закону [6]. Это означает, что передача электрической энергии по токоведущим частям ЛЭП тоже происходит по этому же закону. Это значит, что каждая частотная составляющая электрической энергии вдоль неперегруженной линии электропередачи распространяется по гармоническому закону. По гармоническому же закону распределяются по ЛЭП частотные составляющие напряжения и тока.

Целью работы является определение длины волны электромагнитного поля, распространяемого по токоведущим частям линии электропередачи.

Математическая модель

Традиционно длина волны электромагнитного поля определяется по формуле:

Л =

c f ■ n ’

где c = 300000 км/с - скорость распространения электромагнитного поля в вакууме; n - порядковый номер высших гармонических составляющих; f – частота изменения электромагнитного поля во времени, в России и в странах СНГ принята частота, равная 50 Гц. При такой частоте получается, что длина волны электромагнитного поля равна

Л =

= 6000 км.

Но это в вакууме или разряженной газовой среде. Хотя нередко такая скорость распространения волны электромагнитного поля, а следовательно, и такая длина его волны принимаются справедливым и для иной среды, в том числе и в токоведущих частях ЛЭП.

Но материальная среда, которой обладают токоведущие части линий электропередачи, существенно замедляет скорость распространения электромагнитного поля и сокращает длину его волны.

Из теоретической электротехники известно, что носителями электрической энергии в линиях с распределенными параметрами являются падающие и отраженные волны электромагнитного поля. А скорость передачи каждой волны электромагнитного поля по токоведущим частям ЛЭП определяется фазовой скоростью [7].

Фазовой скоростью v называют скорость, с которой надо перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания. Это скорость перемещения по линии постоянного фазового состояния, каковой может быть только однородная линия электропередачи.

Фазовая скорость волны электромагнитного поля определяется по формуле:

nω ν =     ,

αn где n – номер гармонической составляющей напряжения и тока; ω = 2πf – циклическая частота основной гармонической составляющей; αn – коэффициент фазы n -гармонической составляющей.

Коэффициентом фазы называют мнимую составляющую постоянной распространения электромагнитного поля вдоль однородного участка ЛЭП:

γn = βn + jαn , где γn – постоянная распространения n - гармонической составляющей электромагнитного поля вдоль однородного участка ЛЭП: βn – коэффициент затухания п-й гармонической составляющей волны электромагнитного поля, αn – коэффициент фазы п-й гармонической составляющей волны электромагнитного поля.

Коэффициент затухания β_n несет ответственность за изменение амплитуды волны напряжения и тока при передаче электрической энергии по линейному проводу ЛЭП.

Коэффициент фазы α_n несет ответственность за изменение углов сдвига фаз напряжения и тока, за величины фазовой скорости и длины волны электромагнитного поля [8].

Величина постоянной распространения гармонической составляющей вдоль однородного участка ЛЭП зависит только от ее параметров и не зависит от напряжения и тока. Она может быть рассчитана по известной методике [3, 7, 8].

Получается, что электромагнитное поле по токоведущим частям ЛЭП распространяется с фазовой со скоростью, которая заметно меньше, чем скорость распространения этого поля в вакууме.

В таком случае величину длины волны электромагнитного поля, распространяющегося по токоведущим частям ЛЭП, перефразируя формулу (1), определяют следующим образом:

λ = ^v f

.

Результаты моделирования

Расчеты показали, что постоянная распространения электромагнитного поля вдоль однородного участка ЛЭП однопроводного исполнения с глухозаземленной нейтралью, которая обычно используется для передачи электрической энергии напряжением ниже 1000 В, на частоте основной гармонической составляющей может быть равна γ = (0,0008 + j0,0013) км-1. Это означает, что коэффициент затухания волн напряжения и тока в рассматриваемом случае оказывается равным в = 0,0008 км-1, а коэффициент фазы -а1 = 0,0013 км-1.

Исследуемый однородный участок ЛЭП характеризуется следующими параметрами: погонным активным сопротивлением R 0 = 0,74 Ом/км, собственной индуктивностью

L 0 = 1,28 мГн/км, активной проводимостью G 0 = 10 ¹⁶ См/км и емкостью C 0 = 9 • 10 ⁹ Ф/км.

И тогда фазовая скорость равна (1):

1 • 2п • 50               4     .

v =---------= 24,15 • 10⁴ км/с.

0,0013

В таком случае длина волны электромагнитного поля в ЛЭП определится так (2):

24,15 •Ю4

= 4831 км.

Это длина одной волны электромагнитного поля. Ее отличие от длины волны электромагнитного поля в вакууме составило 1170 км, или 19,5 % (рис. 1).

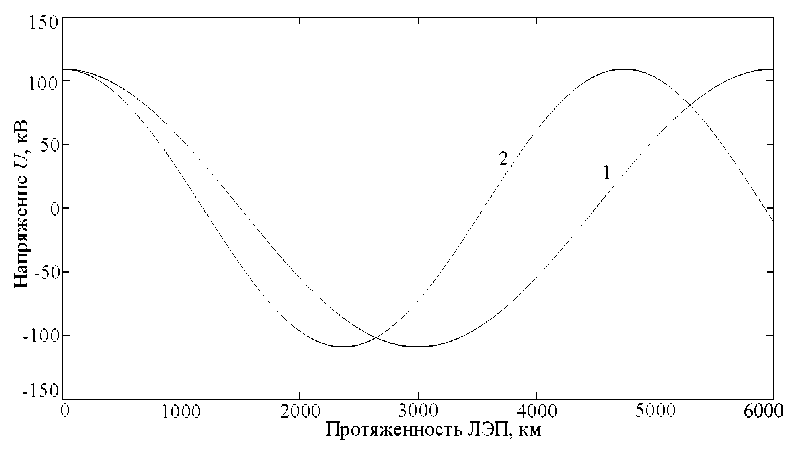
Рисунок 1 - Волны электромагнитного поля: 1 - волна электромагнитного поля в вакууме;

2 - волна электромагнитного поля в ЛЭП

При длине волны 6000 км граница линейности распределения электрической энергии, в пределах которой ЛЭП может приниматься за линию с сосредоточенными параметрами, определяется величиной 240-300 км, а при длине волны 4831 км ЛЭП определяется величиной 193,2-241,5 км.

Передача электрической энергии по ЛЭП однопроводного исполнения обеспечивается одной парой волн электромагнитного поля, двухпроводного исполнения - двумя парами, трехпроводного - тремя, четырехпроводного - четырьмя и т.д. [9, 10]. Электрическая энергия от генерирующих устройств (начало анализируемого участка ЛЭП), которая доставляется электрической нагрузке (конец анализируемого участка ЛЭП), называется падающей волной электромагнитного поля.

Но вся электрическая энергия, доставляемая к концу однородного участка ЛЭП, электрической нагрузкой не потребляется, а в виде отраженной волны электромагнитного поля возвращается обратно к началу участка линии электропередачи.

Напряжение и ток в любой точке линии можно рассматривать как результат наложения двух волн, движущихся в противоположные стороны, - падающей и отраженной. Падающая волна - волна, движущаяся от начала линии к концу. Отраженная - волна, движущаяся от 8

конца линии к началу. Обе они перемещаются во времени вдоль однородного участка ЛЭП с фазовой скоростью v .

Таким образом, в токоведущей части ЛЭП однопроводного исполнения передача электрической обеспечивается результирующей волной электромагнитного поля, получившейся в результате наложения падающей и отраженной волн с одинаковыми фазовыми скоростями, но с разными амплитудами: амплитуда падающей волны электромагнитного поля несомненно больше амплитуды отраженной волны этого же поля. Длина результирующей волны электромагнитного поля может быть сокращена почти в два раза:

a = V, af где а - число волн электромагнитного поля, распространяемого по линейному проводу ЛЭП.

В рассматриваемом случае а= 2. Тогда минимально возможная длина результирующей волны электромагнитного поля, судя по формуле (3), оказывается равной A = 2415,5 км. Хотя теоретически длина результирующей волны электромагнитного поля может изменяться от 2415,5 до 4831 км. Это зависит от фазовых соотношений падающей и отраженной волн. Точную величину результирующей волны электромагнитного поля в многопроводной ЛЭП можно определить в результате анализа результатов передачи электрической энергии по проводам исследуемой линии электропередачи [8].

Передача электрической энергии на десятки и сотни километров обычно выполняется при посредстве высоковольтных ЛЭП трехпроводного исполнения . Передача электрической энергии по таким линиям электропередачи обеспечивается тремя парами волн электромагнитного поля, каждая из которых характеризуется своей постоянной распространения.

При исследовании результатов передачи электрической энергии по ЛЭП-220 кВ трехпроводного исполнения были получены следующие численные значения постоянных распространения для каждой пары волн электромагнитного поля:

Y 1n = ^{(0 -} У Ю) км^-1;

• 7 -    n = ⁽⁰ + ^j ) км^-1;

Y 3 n = ⁽⁰ + j "¹⁰ ) км^-1.

Фазовая скорость тока падающей (отраженной) результирующей волны электромаг- нитного поля даже на частоте основной гармонической составляющей оказывается сравнительно мала (3):

_ 2nnf _ 2 п • 1 • 50

= 67,71 км/с,

= а "  4,64

где а = 3jIm(Y„) • ImY«)' ImY«) = 3/10-1-10 = 4,64 км-1 - усредненный коэффициент фазы, кото- рый можно принять за коэффициент фазы результирующей волны электромагнитного поля.

Результирующая волна результирующего поля есть результат наложения шести волн. Поэтому длина результирующей волны зависит от фазового сдвига этих волн между собой. Формула (4) позволяет определить минимально возможную длину волны:

A nin

v af

67,71 = 0,23

6 • 50

км.

Максимально возможная длина результирующей волны электромагнитного поля определяется по формуле (3):

v    67,71

A™, =— = ---- = 1,35 км.

max    _{f     50}

Длина результирующей волны электромагнитного поля оказалась очень мала. Для ее достоверного выяснения необходимо выполнить анализ результатов передачи по исследуемому однородному участку ЛЭП небольшой протяженности [3, 8]. Например, 10 км. На ос- нове проведенного анализа (рис. 2) построена графическая интерпретация распределения фазного напряжения на частоте основной гармонической составляющей вдоль анализируемой трехфазной линии электропередачи.

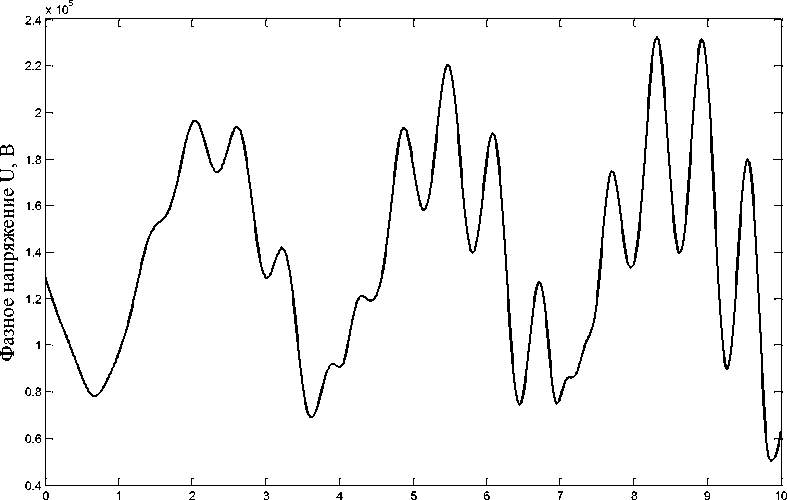
Протяженность от конца ЛЭП, км

Рисунок 2 – Графическая интерпретация распределения фазного напряжения от конца однородного участка ЛЭП трехпроводного исполнения на частоте основной гармонической составляющей

Из рисунка 2 видно, что распределение фазного напряжения вдоль анализируемого участка ЛЭП представляет собой сложный колебательный процесс. Это совокупность колебаний различных амплитуд с вполне стабильным периодом порядка 0,6 км, что означает длину результирующей волны электромагнитного поля, равную 0,6 км. Это вполне соответствует неравенству:

X  = 1,35 км >  A = 0,6 км >  A m = 0,23 км.

max                                      min

Подобный результат визуального определения длины результирующей волны электромагнитного поля может быть получен и из графической интерпретации распределения линейного тока по тому же участку ЛЭП. Численное значение этого результата может отличаться от 0,6 км, но, тем не менее, оно будет удовлетворять неравенству

A x >  A >  A min .

Подобный анализ можно выполнить и для неоднородного участка ЛЭП или даже для всей линии электропередачи [11].

Заключение

Предлагаемая методика определения длины волны электромагнитного поля в материальной среде, которой являются токоведущие части линий электропередачи, внесет существенную коррекцию в волновую теорию распределения электрической энергии и повысит достоверность анализа ее передачи потребителю.