Двумерное математическое моделирование диаграмм электрокаротажа на основе вычислений на графических процессорах

тивных высокопроизводительных программ численного моделирования.

Существующая интерпретационная база электрокаротажа основывается на решениях прямых и обратных задач в рамках одномерных слоистых моделей сред. Однако при интерпретации на интервалах пластов сравнительно небольшой мощности возникает неоднозначность в определении удельной электропроводности. Электрокаротажные сигналы в маломощных пластах с неравномерным пространственным распределением удельной электропроводности могут быть адекватно проинтерпретированы только в рамках многомерных моделей. Использование решений двух- и трехмерных задач в полной постановке оказывается малоэффективным по причине их высокой ресурсоемкости. Для сокращения времени вычислений прибегают к параллельным исполнениям алгоритмов на кластерах и многопроцессорных вычислительных системах. Данный подход эффективен, но он не может быть использован для интерпретации в производственных условиях, а также для создания автоматизированных интерпретационных систем.

Современные графические процессоры, созданные для быстрой обработки большого объема графических данных, эффективно используются для ускорения вычислений при решении задач каротажа. Одной из технологий, позволяющих производить неграфические вычисления на GPU, является NVidia CUDA (Compute Unified Device Architecture). В данной технологии используется блочносеточное представление потоков исполнения, что способствует упрощению реализации алгоритмов, ориентированных на работу с многомерными данными. Технология CUDA предоставляет возможность работы с различными типами памяти, имеющими существенные различия в латентности, доступности, объемах и прочих характеристиках. Эффективное использование возможностей данной технологии позволяет достичь существенного ускорения вычислений.

Целью данной работы является развитие математического моделирования данных электрокаротажа нефтегазовых скважин с использованием высокопроизводительных параллельных вычислений на графических процессорах. Для достижения поставленной цели необходимо выполнить следующие задачи:

• 1)    реализовать эффективные параллельные алгоритмы численного решения двумерной прямой задачи электрокаротажа с использованием метода конечных разностей;

• 2)    провести математическое моделирование диаграмм электрокаротажа и сравнительный анализ производительности вычислений на графических процессорах.

Основные особенности решения поставленных задач состоят в следующем. Численное решение двумерной прямой задачи электрокаротажа на основе метода конечных разностей сводится к системе линейных алгебраических уравнений с пятидиагональной матрицей. Для ее решения применяются прямой метод квадратного корня и итерационный метод сопряженных градиентов. Для преодо- ления слабой обусловленности матрицы используется предобуславливание. Разработка параллельных алгоритмов сопровождается оценкой быстродействий и математическим моделированием в типичных геоэлектриче-ских моделях нефтегазовых пластов.

Рассматривается двумерная осесимметричная геоэлектрическая модель, представленная пластами с горизонтальными границами, в каждом из которых при вскрытии скважиной образуется зона, обусловленная проникновением фильтрата бурового раствора.

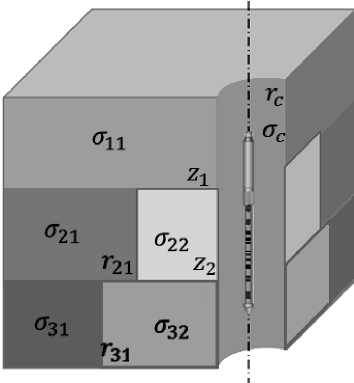
Рис. 1 . Двумерная осесимметричная геоэлектрическая модель

Геоэлектрическая модель в цилиндрической системе координат {r, <р, z} имеет следующее описание. Ось z совпадает с осью симметрии (центр скважины). Горизонтальные границы пластов описываются уравнениями вида z = zk, к = 1,...,n-1, где n - число пластов. Уравнение l -й цилиндрической границы к -го пласта: r = rk z. При пересечении горизонтальных и вертикальных границ образуются тороиды с прямоугольным сечением, которые характеризуются своим значением удельной электропроводности ак. . Будем полагать, что удельная электропроводность бурового раствора в скважине постоянна и равна (аг 0 = стс). В остальной части среды электропроводность является функцией двух переменных а(r, z). Двумерная модель представлена на рис. 1.

При решении прямой задачи электрокаротажа исходным является уравнение Пуассона. Граничные условия включают равенство потенциалов и непрерывность нормальной компоненты плотности тока на границах раздела областей.

В среде с распределением проводимости о ( r , z ) значение потенциала в точке может быть представлено в виде суммы

U = U^a + U ⁰, где U ^a отвечает за аномальную составляющую, а U⁰ - за первичную, зависящую от источника поля, расположенного в однородной среде с проводимостью а ₀.

Вычисление значения первичного потенциала в точке на оси скважины производится аналитически, так как скважина заполнена буровым раствором с известной проводимостью, а источник может быть представлен в виде точечного

виду. Подробное описание данного подхода дано в работе [1].

В итоге получаем СЛАУ большой размерности с матрицей в представленном на рис. 2 виде.

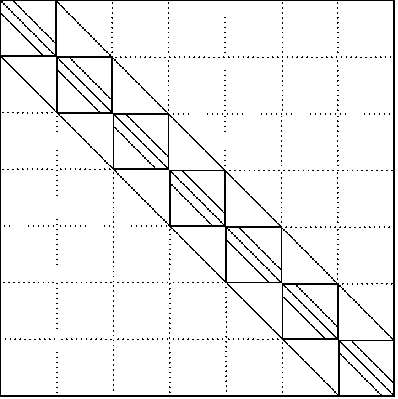
Рис. 2. Итоговый вид матрицы

U0

I

4па 0 R ’

где I - сила тока, R = rr ² + z ² .

Для поиска аномальной составляющей поля необходимо записать разность уравнений непрерывности плотности токов, соответствующих полному и первичному потенциалам [1 ],

div ( oV U^a ) = - div (( а - a ₀) V U ⁰) .   (2.1)

В цилиндрической системе координат уравнение (2.1) сводится к следующему:

1 д

r д r

\

дUa} or--- д r J

д

+ — а

д z

1F (aо r д r

—

a) r

\

( дUa ^

I   дz J

U^

д r

⁺F ^{( a} о д z

\

^a )

д U ⁰ ^

д z

(2.2)

После чего к уравнению (2.2) применяется конечно-разностная схема. В результате задача поиска потенциала в точке сводится к решению системы линейных алгебраических уравнений (СЛАУ) с пятидиагональной положительно определенной матрицей, которая в последующем приводится к симметричному

Поставленная задача выполняется в два этапа: создание СЛАУ по известной модели среды и ее решение. Вычисление удельных сопротивлений на данной глубине производится по полученным значениям потенциалов в точках и не является ресурсоемкой операцией.

Для вычисления матрицы и правой части СЛАУ используется преимущественно графическое устройство. В рамках данного этапа существуют узкие для параллелизма места, которые не могут быть вычислены параллельным алгоритмом. По этой причине их вычисление производится на ЦПУ. Так как все данные изначально считываются в память ЦПУ, а вычисление узких мест требует только начальные данные, то шина используется для передачи результата на графическое устройство.

Наиболее ресурсоемким является решение СЛАУ. Были рассмотрены прямой и итерационный методы. В качестве итерационного был рассмотрен метод сопряженных градиентов с предобуславливателем, который хорошо подходит для исполнения на графических устройствах, так как все используемые операции (умножение вектора на матрицу, сложение и скалярное умножение векторов) хорошо параллелятся. Итерационный метод рассматривается с различными предобуслав-

ливателями, в том числе полученными с использованием алгоритма Хотеллинга [2]. Прямой метод квадратного корня хорошо зарекомендовал себя при последовательных исполнениях, но имеет много узких мест при параллельной реализации.

• 3.1.    Метод квадратного корня

• 3.2.    Метод сопряженных градиентов с предобуславливателем

Решение СЛАУ прямым методом квадратного корня заключается в вычислении треугольной матрицы с последующим решением двух систем на ее основе.

При нахождении верхней треугольной матрицы S вычисление элементов каждой строки может производиться параллельно при известном диагональном элементе, который вычисляется при известной верхней строке. В результате возникают зависимости на порядок исполнения среди строк и элементов строки (диагональный элемент должен быть вычислен первым в строке). По этим причинам появляются ограничения, не позволяющие использовать графическое устройство эффективно.

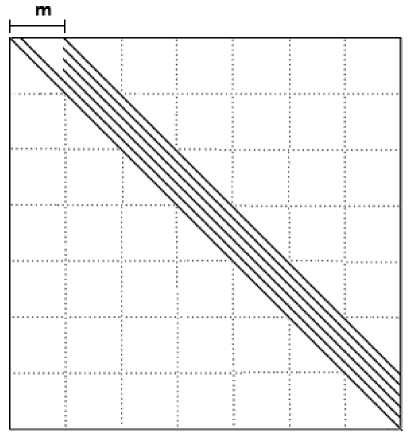
Рис. 3. Верхняя треугольная матрица при решении СЛАУ методом квадратного корня

Из рекуррентных соотношений вычисления верхней диагональной матрицы S [3] следует, что она будет иметь вид, представленный на рис. 3. Если использовать это при вычислении первых m строк, то нулевые элементы не будут участвовать в расчете неизвестных. Знание вида искомой матрицы устраняет необходимость вычисления элементов, находящихся на m+1 диагонали и далее от главной (рис. 3). В процессе решения методом квадратного корня неоднократно необходимо суммировать массивы чисел, что может быть параллельно исполнено использованием редукции относительно операции суммирования.

С помощью технологии NVidia CUDA на графических процессорах могут быть эффективно выполнены операции взятия нормы, сложения и скалярного произведения векторов, умножения матрицы на вектор. Данные операции реализованы в библиотеки CUBLAS и были использованы при применении данного метода. По причине специфического вида матрицы СЛАУ использование предложенного в CUBLAS алгоритма умножения матрицы на вектор было неэффективным.

Данная операция была реализована с учетом ее особенностей: в вычислении участвуют только ненулевые диагонали, обращения к нулевым диагоналям не происходит.

При решении СЛАУ методом сопряженных градиентов с предобуславливателем необходимо некоторое начальное приближение, в качестве которого изначально выступает нулевой вектор, а в дальнейшем это результирующий вектор для предыдущего положения каротажного зонда в скважине. Данный подход позволяет существенно уменьшить число итераций метода при движении в пределах одного пласта.

Изначально на каждой итерации вычисляется произведение предобуславливателя на правую часть системы, что позволяет избавиться от хранения предобуслвливающей матрицы. После чего исполняются операции метода, в результате которых получаем вектор решения.

• 4.    Численные результаты

Применительно к решению двумерной прямой задачи электрокаротажа получены оценки производительности при последовательных вычислениях на CPU и параллельных на GPU с использованием описанных алгоритмов.

method

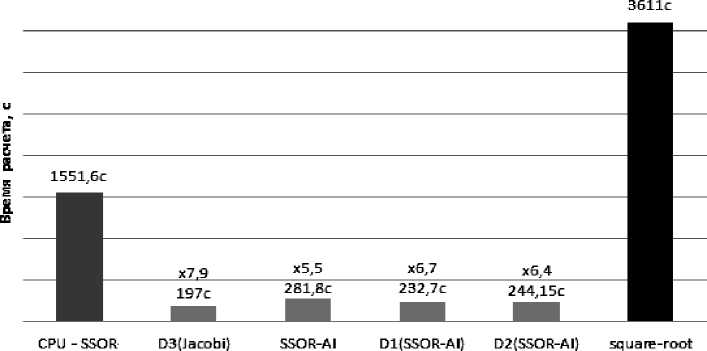
Рис. 4. Производительность алгоритмов решения прямой задачи электрокаротажа при вычислениях по профилю скважины с использованием Quad Q9300 и GTX 480

На рис. 4 представлены времена расчета диаграмм электрокаротажа по профилю скважины. В качестве времени исполнения на ЦПУ было взято время исполнения алгоритма, в основе которого лежит метод сопряженных градиентов с предобуславливателем SSOR. Лучшее время показал параллельный алгоритм, также основанный на методе сопряженных градиентов с предобуславливате-лем. В качестве предобуславливателя использовался третий элемент последовательности, полученной по алгоритму Хотеллинга с начальным приближением в виде Якоби [2]. Время исполнения алгоритма, основанного на методе квадратного корня, представлено правым столбцом, и его неэффективность оче- видна. В данном случае диаграммы состоят из 300 точек положений источников и приемников. Как видно, параллельные алгоритмы на основе метода сопряженных градиентов с предобуславливателем дают существенный прирост производительности (~8 раз).

На рис. 5 представлено сравнение быстродействий различных видеокарт при расчете диаграммы электрокаротажа в двумерной модели. Видно, что времена расчета сигналов электрокаротажа при движении по профилю достаточно сильно зависят от типа используемого устройства. Отличия быстродействий заключаются в различном количестве и тактовой частоте мультипроцессоров. Численные результаты указывают, что реализованные ал-

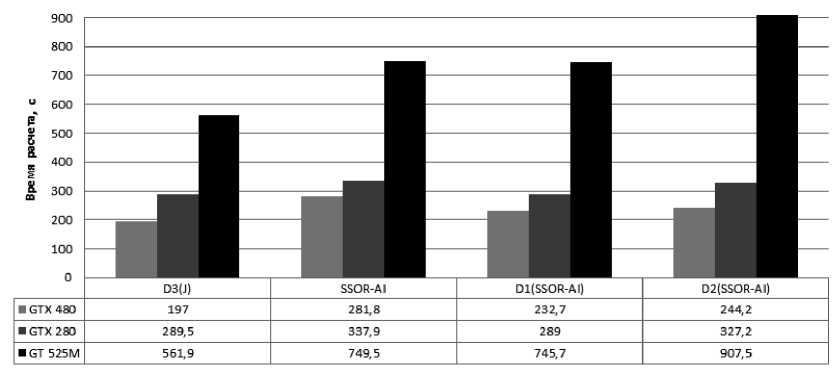
Рис. 5 . Производительность алгоритмов при исполнении на различных видеокартах

горитмы являются хорошей альтернативой существующим на данный момент последовательным алгоритмам решения двумерной прямой задачи электрокаротажа.

Все вышеприведенные результирующие времена расчетов получены при работе на подробной сетке, необходимой для детальных исследований. Данная сетка содержит 249 точек по ^r , расстояние между которыми растет с нелинейным шагом в направлении от оси симметрии. По оси ^z сетка включает 308 точек с увеличением нелинейного шага от источника в положительном и отрицательном направлениях. При этом в верхней полуплоскости данная сетка содержит 56 точек с быстро растущим шагом, в другом случае – 251 точку с медленно растущим шагом. Выбор нелинейного шага определяется затуханием электрического поля при удалении от источника со скоростью 1 / r ² .

• 5.    Моделирование диаграмм

С использованием разработанных параллельных алгоритмов на GPU проведено математическое моделирование диаграмм электрокаротажа в двумерных средах.

Как уже указывалось, двумерное моделирование необходимо для изучения маломощных пластов (меньше длины зонда). Проанализируем геоэлектрические модели и диаграммы электрокаротажа, характерные для разрезов нефтегазовых месторождений. Рассматривается двумерная модель нефтенасыщенного пласта, перекрытого глинистыми и подстилаемого водонасыщенными отложениями. Горные породы вскрыты скважиной с пресным буровым раствором (2 Ом∙м). Нефтенасыщенный пласт мощностью 5 м имеет удельное сопротивление 25 Ом∙м и включает зону проникновения (15 Ом∙м), образованную проникновением фильтрата бурового раствора в пласт глубиной 0.4 м. Подстилающий водонасыщенный пласт имеет удельное сопротивление 5 Ом∙м и характеризуется повышающей зоной проникновения (20 Ом∙м) глубиной 0.5 м. Перекрывающие глинистые отложения имеют удельное сопротивление 3.5 Ом∙м.

На рис. 6 представлены диаграммы трансформации сигналов электрокаротажа, полученные в модели нефтенасыщенного пласта. Трансформация сигналов осуществляется в рамках однородной среды в соответствии с (2.2). Как уже указывалось, зонды электрокаротажа характеризуются различной длиной и расстоянием между источником и приемником. Рассмотрим зонд A2.0M0.5N со следующими параметрами: расстояние между источником и первым (ближним к источнику) приемником равно 2.0 м, а расстояние между приемниками – 0.5 м. Исследуя диаграммы нескольких зондов электрокаротажа, можно строить более точные и обоснованные суждения о пространственном распределении удельной электропроводности горных пород, окружающих скважину, чем при использовании одного зонда.

В глинистых отложениях значение кажущегося сопротивления зонда A2.0M0.5N составляет около 4 Ом∙м, на интервалах неф-

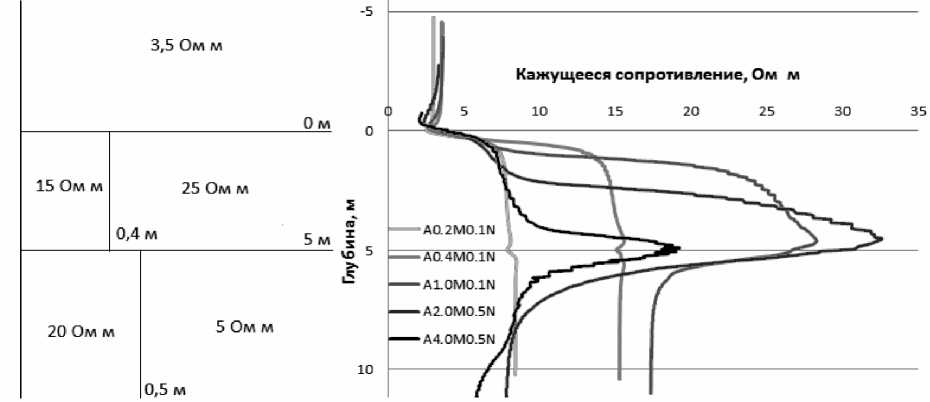
Рис. 6. Типичная двумерная модель и диаграммы электрокаротажа, полученные на основе параллельных вычислений на GPU

те- и водонасыщенных пластов – порядка 15 Ом∙м, в то время как сопротивление нефтенасыщенного пласта 25 Ом∙м, водонасыщенного – 5 Ом∙м. Это указывает на то, что на показания зонда существенное влияние оказывают скважина и промытая прискваженная зона. Низкие значения сопротивления в кровле нефтенасыщенного пласта связаны с влиянием на сигналы глинистых отложений.

Реализованные параллельные алгоритмы являются эффективным инструментом для интерпретации данных электрокаротажа в сложных геологических моделях нефтегазовых скважин.

Основным научным результатом работы является реализация параллельных алгоритмов математического моделирования данных электрокаротажа в нефтегазовых скважинах для высокопроизводительных вычислений на графических процессорах. Проведенные научные исследования позволили сделать следующие основные выводы.

Двумерная прямая задача электрокаротажа на основе метода конечных разностей сводится к системе линейных алгебраических уравнений с пятидиагональной матрицей, для решения которой применены прямой и итерационный методы. Метод квадратного корня, успешно применяемый для последовательно решаемой задачи, оказывается слабоэффективным при параллельном решении на GPU. Однако диагональный вид матрицы позволяет существенно сократить количество операций и применить метод сопряженных градиентов с предобуславливателем, где основные операции умножения матрицы на вектор и скалярного произведения векторов хорошо распараллеливается. Реализованы алгоритмы с использованием предобуславливателей Jacobi, SSOR-AI и их модификации, вычисленные с помощью алгоритма Хотеллинга.

Получены оценки быстродействий при расчетах диаграмм электрокаротажа в дву- мерных геоэлектрических моделях при вычислениях на CPU и GPU. Показано, что при использовании GPU для вычислений удается увеличить производительность примерно в 8 раз по сравнению с идентичными расчетами на CPU. При этом лучшие результаты при решении СЛАУ методом сопряженных градиентов с предобуславливателем получены при использовании в качестве предобуславлива-теля третьего элемента из последовательности предобуславливателей Хотеллинга с начальным приближением в виде Jacobi. Отмечено, что увеличение производительности реализованных алгоритмов существенно зависит от сложности исходной модели и размеров выбранной расчетной области.

Проведено математическое моделирование и сравнительный анализ диаграмм электрокаротажа и изучены основные особенности их поведения в типичных разрезах нефтегазовых скважин. Выполненный объем численного моделирования показал высокую эффективность разработанных алгоритмов, что указывает на возможности создания автоматизированных систем интерпретации нового поколения, использующих ресурсы GPU.