Dynamic selection approach to overcome the demotivation of learners in a community learning system

In the field of learning, collaborative approaches aim at promoting collaboration between peers allowing them to exchange and share skills for achieving a common project. We then talk about collaborative learning, collaborative work, collaborative training and collaborative culture [1]. Considering, in addition, community management of knowledge, the collaboration can have a common learning objective: each community member performs a part of the overall task using his individual resources or those of the group. This is referred to as learning communities or Communities of Practice (CoPs).

The current advancement of Information and Communication Technologies (ICT) provides many opportunities for the design and development of computer systems that support Communities of Practice [2][3]. In this case, they are called virtual communities. *Communities of Practice refer to groups of professionals gathered to share and exchange explicit and tacit knowledge related to their field of intervention.

In this context, the communication plays an important role in the learning process since the interaction among the CoP members is the primary mean through which learning takes place. In particular, in a virtual CoP, members may not physically know each other but just through their interactions. Therefore, a CoP member, considered as a learner, expresses ideas to share with other members, establishes links between the expressed ideas (his own ideas and those of the others), structures them in order to bring out new ones and, finally, build knowledge.

The community aspect of learning through a virtual CoP generates a big number of aid requests and exchanges between members. All of these data streams are visible to all of the CoP members while these latters may not be able to answer most of the posted requests. This lead, in some cases, to the demotivation of members to participate to the interactions and sometimes to the disengagement towards the CoP.

On the other hand, the constitution of groups plays an important role in the success of collaborative learning. Indeed, in the case of a formal learning, learners are usually subdivided into a set of small workgroups. The teacher plays the role of a facilitator (tutor) who guides the learners to the appropriate resources supporting the collaboration, but also the role of an animator who makes decisions about the interaction strategies inside and between the groups.

In this context, we propose a dynamic approach to forming homogeneous groups within a CoP dedicated to community problem solving. Specifically, groups are formed through a dynamic selection of a set of CoP members that we consider the most likely to contribute to the resolution of a specific problem. Dynamicity of the selection is based on the degree of activity of these members in solving similar problems in the past.

Section 2 of this paper presents a state of the art on communities of practice and on group formation. Section 3 introduces the problem. In Section 4, we present the principle of our members’ selection approach and the related context modelling. Section 5 describes in detail the proposed filtering and traces analysis algorithms. Finally, we present in section 6, the conducted experiments to validate our approach.

II.    Related Works

• A.    Communities of Practice

CoPs are defined by E. Wenger [4][5] as “a group of people who share a concern or a passion for something they do and learn how to do it better as they interact regularly”. In [5], E. Wenger defines a model of a CoP structured around three main components: the domain (members of a CoP have a shared domain of interest that distinguish them from other people), the community (the members should help each other and engage in activities, discussions, etc.) and the practice, which represents the memory of the community (experiences, tools, stories, techniques to solve problems, etc.).

A CoP is a social structure of knowledge that fosters the sharing of this knowledge between members and allowing the emergence of a collective intelligence. Learning is the first mission of a CoP and this latter is considered as the perfect place to do it. Indeed, learning is taking place socially through exchanges of ideas between members allowing them to build the community identity. The social learning is ensured by the balance between the participation process (exchange, sharing and confrontation of ideas inducing the generation of knowledge) and the reification (formalization of the CoP built knowledge in concrete artifacts as texts or other types of productions).

The communication and exchanges in the frame of a CoP have always been realized through direct person-to-person interactions in a close environment [6]. With the current advent and progress of Information and Communication Technologies (ICTs) and their use to support interactions, virtual CoPs appeared. A CoP is called virtual when its members use ICT as the main mode of interaction [7]. Virtualization does not exclude the use of face-to-face meetings, however, several factors, including the geographical dispersion and busy schedules encouraged the virtualization and made communication through ICTs very effective [7].

• B.    Group formation in collaborative learning systems

According to Lipponen [8], collaborative learning supported by ICT is focused on the way collaboration and technology can, on one hand, improve interactions and group work, on the other hand, facilitate the sharing and distribution of knowledge and expertise among community members. In this context, the contribution of ICT is seen as the integration of adaptive and intelligent functionalities on collaborative learning systems. Indeed, an adaptive learning system is a system that aims to adapt some of its functionalities, such as the presentation of content or the support to navigation, to the needs and preferences of the learner. An intelligent learning system aims to provide the learner with a support during the problem-solving process, as a human tutor would do [9].

However, there are collaborative learning systems that combine both adaptive and intelligent functionalities. These latter can be used for the group formation, to provide domain-specific support or to provide peer interaction support [10]. The group formation in a collaborative learning system is important to make learning more effective, foster the collaboration and increase productivity of the exchanges. Indeed, Chen considers the group formation as crucial for triggering productive peer interactions [11].

The state of the art related to group formation shows that most of the systems propose to form heterogeneous groups based on the learning styles of learners [12]. The idea behind this is that the heterogeneity of the group promotes efficient interactions among peers [13][14].

Generally, the data of a learner are represented according to a set of attributes and are retrieved using his profile and/or questionnaires. There are three strategies to form groups according to the values of these attributes: 1) homogeneous grouping where the attributes’ values for learners of the same group must be homogeneous, 2) heterogeneous grouping where these values must be heterogeneous, 3) mixed grouping where the values must be homogeneous for some attributes and heterogeneous for others.

The homogeneous grouping is performed using classification techniques or methods specific to the learning context based on similarity calculation. These same techniques can be adopted in the context of heterogeneous grouping by creating first homogeneous groups, and then taking a learner from each group to form a heterogeneous group. Generally, the heterogeneous and mixed groupings are considered as optimization problems and therefore optimization methods, such as genetic algorithms, are used to find the best possible combinations [15][16].

• C.    Research works on group formation

We provide in this paragraph a list of works from the literature that addressed the group formation problem in collaborative learning systems.

TANGOW [14] is a web-based learning system that proposes to learners, individual and collaborative activities. The objective of forming groups in this work is to increase the group productivity bringing closer learners with reflective learning style and learners with active learning style.

NUCLEO [17] is a system that simulates a virtual world in the form of a role-based game in which learners are grouped into teams to perform missions. This system is based on the Vermunt learning style model [18] to form the groups. The aim is to bring together, in the same group, learners with complementary learning styles.

AUTO-COLLEAGUE [19] is a system that supports learning of UML course. To form groups, it uses a model of the user that consists of: 1) The level of expertise that describes the knowledge on UML, 2) The Performances of the user behavior and 3) the personality, which is related to the characteristics that influence the behavior of the learner. The trainer defines the constraints guiding the formation of groups. Thus, the system is based on a genetic algorithm called "simulated annealing" to find the best groups compositions according to the defined constraints.

WikiClassroom [20] is a collaborative wiki that provides learners with an interface to write and revise pages and a forum to discuss their ideas during the collaboration. The system traces the learner's activities in order to build a model representing his contributions to the group. In order to form heterogeneous groups, the system assigns to each learner an intelligent agent that uses a Bayesian Network to probabilistically estimate the contribution of a learner towards his group’s Wiki.

MATHEMA [21] is an adaptive hypermedia system that aims to support the learning of electromagnetism individually and/or in collaboration. To form the groups, this system is based on a predefined learning style in combination with the level of knowledge related to the objective of learning. It presents then to the learner a list of candidate collaborators (the most recommended), sorted according to the learning style. The learners having the same learning style are sorted according to the level of knowledge related to the objective of learning. The groups are formed manually by the learner who chooses with whom to collaborate.

The works of Brauer and Schmidt [22] focus on an online social network of learning in which the user decides to initiate a collaborative work. The system then searches for candidates and proposes groups. The group formation is based on: 1) the availability, 2) the learning style and 3) the knowledge model represented by weighted tags. The aim is to select the members having a common learning style, a high score in the knowledge related to the proposed subject, and a low distance in the social network regarding the initiator. To find the best possible solutions, a genetic algorithm is used.

In the works of Jagadish [23], a K-NN classification algorithm was used to subdivide learners into groups, based on the personalities traits and their learning styles. The formed groups of learners can discuss via the chat module of Moodle about a course and/or specific activities. The data on which the algorithm is based are derived from the learners’ profiles and questionnaires completed by the learners.

Finally, Duque and Gómez-Pérez [24] offer to the teacher a method that allows him to form groups of learners, homogeneous or heterogeneous, according to his own criteria based on the way in which these learners solve academic tasks. This method uses a set of indicators on how learners solve academic tasks. The system analyses their collaboration and interactions and uses the concept of "Data depth" to measure the similarity between the values of these indicators in order to form groups. The teacher should have specified heterogeneous and/or homogeneous indicators before using the method. The values of the used indicators can be built from actions performed by learners or derived from questionnaires they completed and entered manually.

III.    What is the Problem?

• A.    A problem of demotivation

ICT environments supporting CoPs aim at helping learners to improve their interactions in order to make learning more effective. In the case of a CoP dedicated to community problem solving, when a member encounters a problem, the others offer him this help in order to achieve a solution that he judges acceptable to his problem. Learning is then mainly an increase of knowhow through exchanges and interactions between the CoP members until the problem is solved.

However, the social nature of learning through a CoP requires the community to be active and its members’ interactions to be maintained as long as possible. In other words, if the CoP has been abandoned by its members, no more learning is possible. According to Wenger et al., only 25% of members represent the hard core of a CoP, 30% are considered as active members who participate less regularly, while 45% are considered as peripheral members who typically learn by observing the interactions between the core and the active members [25]. In our previous works, we have identified the main demotivating factors that can lead to a lack of participation of members to the community interactions [15][26][27]. We summarize them in the following points:

• •    Receiving, by a member, repeated aid requests related to similar problems or to problems already solved in the past,

• •    The response time to an aid request, when it is long, isolate the requesting member and demotivate him to continue his interactions within the CoP,

• •    The preference of members to use standard tools of interaction instead of investing to become familiar with a new interface of the CoP interaction tool (as simple as it could be).

• B.    A partial solution through NICOLAT

To this end, we designed and implemented a Community Mobile and Adaptive System (NICOLAT: French Acronym of "système iNformatIque COmmunautaire mobiLe et AdapTatif"), a generic tool supporting the interactions of a CoP adapted to the domain and the practice of any target learning community. We offer through this system features allowing to minimize  the demotivating  factors cited  above.

NICOLAT system is composed of 4 layers: the

“Community” layer, the “Problem Resolution” (PR) layer, the “Adaptation of Interactions” (AI) layer and the “Interface” layer (Fig. 1).

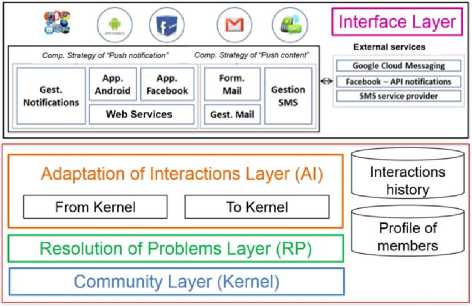
Fig.1. The 4 layers of NICOLAT System

The “Community” layer constitutes the kernel of the system. It corresponds to a web 2.0 environment in the form of a social network. The interactions take place through threads supporting the discussions around problems faced by community members [28].

The aim of the “Problem Resolution” layer is to exploit the history of solved problems in order to automatically propose to the CoP members solutions from similar problems that were solved in the past based on the CBR (Case Based Reasoning) cycle. When the member is not satisfied with any of these solutions, the problem is posted to the other members through the community layer [29][30].

The “Adaptation of Interactions” layer is designed to overcome two demotivating factors: i) minimize the response time after posting an aid request requiring a rapid response and ii) overcome the problems of handling new interaction tools [31]. Indeed, this layer supports access to the community core of NICOLAT through several standard social and mobile interaction tools frequently used by the CoP members. For example, a member participating in a discussion thread may publish his contribution and consult the publications of other members by sending messages directly from his usual email box, his Facebook account or through the available NICOLAT Android and iOS apps. When there is no connectivity to Internet, the member can also interact with the NICOLAT kernel through SMS. The AI layer implements technological bridges which transform the exchanged content between the considered interaction tools formats and the internal format of NICOLAT kernel (features "From Kernel" and "To Kernel" in the figure 1).

The “Interface” layer ensures communication between the AI layer and a CoP member. It provides to the AI layer, software components able to transmit and retrieve data from and to the system. These components are grouped into: i) community components (Facebook application and component dedicated to interaction with email clients); and ii) mobile components (Android app, iOS app and a software component able to send and receive SMSs).

• C.    A problem of orchestration

Minimization of the response time and improvement of accessibility to the community environment through the adaptation of interactions are the two main strengths of NICOLAT. They allow to encourage the collaboration and to increase the motivation for mutual aid and then to enhance the learning among the CoP members.

However, after conducting an experiment of NICOLAT system within real CoP members, two other demotivating factors appeared. We summarize them in the following two points:

• •    First, adapting the interactions according to the AI layer vision, results in flooding the workspace of a CoP member with new data over time. Indeed, a single publication in a thread generates a large number of notifications to all members of the CoP, in every interaction tool they use. Therefore, a member who is in permanent contact with the CoP activities will receive notifications via Facebook, via the mobile app on his smartphone and/or tablet and will also receive notifications via SMS and email. These notifications are considered as unnecessary in most of the cases.

• •    Furthermore, all members of the CoP may not be able to solve every type of problems. In particular, when posted by more experienced members. A member is then demotivated if he is called to solve problems while he is not able to do it. Vice versa, a member asking help and hoping to receive a response as soon as possible may be involved in solving other problems for which, he might not be able to give a positive contribution.

To overcome these inconveniences, we propose to add to NICOLAT architecture a “selection of members’ layer” having the aim to select a minimum group of members to whom send a problem notification when it is posted. This layer implements our selection approach and is based on a static and dynamic selection that we will explain in the following paragraphs (Fig. 2).

Interface Layer

Selection of Members Layer Context management |1 Staticselection

Dynamic selection

Filtering Traces analysis

Adaptation of Interactions Layer (Al)

Resolution of Problems Layer (RP)

Community Layer (Kernel)

Fig.2. Components of the AI layer.

IV.    Our Approach for Selecting Members

• A.    Principle

In order to avoid involving all of the CoP members in each discussion, we propose hereafter, an approach for selecting members to whom send an aid request, that we consider as the most likely to contribute positively to solve the corresponding problem. The other members, supposed to be not able to contribute to the resolution of this problem, will benefit from this experience when they face a similar problem in the future or just by consulting the in-progress discussions.

To do this, we first use a set of static rules, modelling the domain knowledge of the CoP. Indeed, depending on the members’ levels of expertise, these rules define who is able to solve which type of problem. However, they do not take into consideration the new skills acquired by a member during his previous interactions and his learning from the CoP. Indeed, according to the principle of community learning, more a member is active, more he acquires new skills to solve new kinds of problems. Therefore, in addition to the static rules, we propose to analyze, dynamically, the previous contributions of members in order to select those who were the most active in a context similar to the context of the target problem.

Our group formation is then based on two complementary selections: static and dynamic (Fig. 3).

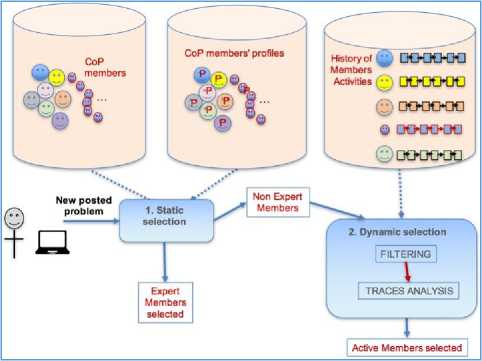
Fig.3. Static and dynamic selections.

When a problem is published, the static selection allows defining a set of members to be solicited based on their profiles, while the dynamic selection evaluates the past activities of statically not selected members in order to complement this list by other members with relevant contributions and active profiles.

Our dynamic selection of members is a problem of forming homogeneous groups around the posted problem. In the related works presented in the state of the art, members data are represented as vectors. The groups are formed synchronously using clustering algorithms for the homogeneous groups and genetic algorithms for example for inhomogeneous groups. In our case, we are interested to form a single group at a time. Our groups are then formed asynchronously while a CoP member can belong to several groups simultaneously.

• B.    Context modeling

In our CoP learning situation, we consider two dimensions of the context: the problem context and the member context. The member may be the one who posted the problem or the member candidate to be selected to solve it. We represent the member context by his two profiles:

• 1)    Domain-related profile, is a set of key-value attributes representing the specialty and expertise of a member in relation with the domain of the CoP.

• 2)    Technological profile, specifies the member interaction tools, his availability related to each tool as well as technical information to contact him using these tools (login for mail, the server number to which to send the SMS, etc.). Once the member is selected, this profile is used to decide which interaction tool is to be used to solicit him.

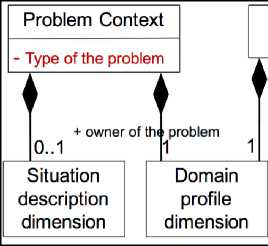
In order to support the genericity with regard to the domain of a CoP, we represent a problem according to four dimensions:

• 1)    Type of problem, serving to classify the problems according to the CoP Domain.

• 2)    Description of the situation where the problem has occurred. It consists of a set of key-value attributes related to the domain of the CoP.

• 3)    Textual description of the problem, as it was written by the CoP member when he submitted his aid request. This dimension is exploited by the problem resolution layer to look for similar problems already solved in the past.

• 4)    Domain profile of the requester member, in particular, his specialty and his level of expertise

In summary, Fig. 4 below, represent a class diagram that shows all of the considered dimensions of the learning context in a CoP supported by NICOLAT.

Member

Context

___________1^__________

Technological profile dimension

Fig.4. Learning context model in a CoP supported by NICOLAT.

We note that the data of the member-related context are stored in the system and the data related to the problem are collected from the requesting member when he published his problem through an online form.

• C.    Static selection

The static selection consists of matching the profiles of all members with the target problem context and the profile of the requesting member, in order to select only the members who are able to solve the problem. To this end, we apply rules whose generic structure is composed of two parts:

• •    IN part, which includes a set of conditions on the problem and the requester. If the target problem and its requester’s profile meet the criteria of one "IN" element, the rule is applicable.

• •    OUT part, which includes conditions on the profiles of the members to be selected. If the profile of a CoP member meets the condition of one "OUT" element, he will be selected.

• D.    Dynamic selection

Contributions of the members represent the comments posted in the corresponding problem thread. At the end of discussion and after solving the problem, the system asks the requesting member to specify the relevance of the different comments that helped him to solve his problem in order to form traces. These contributions’ traces are stored in traces files and concern only the comments considered relevant.

Furthermore, we assign a weight to each context attribute, for each type of problem. A weight is a binary number that characterizes the degree of importance of an attribute with regard to a problem of a given type: “0” means that the attribute is not relevant while “1” means that it is relevant. The allocation of weights is performed by the CoP expert members.

Therefore, after traces analysis, a member is selected if he has a sufficient number of contributions related to problems whose context is similar to the target problem. This number must be greater than or equal to a minimum that we call contributions threshold (ConThreshold) defined, for each type of problem, by the CoP experts. For example, if ConThreshold(X) = 6, the member to be selected to participate in the resolution of a problem of type 'X' must have had in the past, at least, 6 contributions in solving similar problems to the target problem.

The dynamic selection consists then in searching, for each member of the CoP, for the problems similar to the target problem, to which he has given relevant contributions. If the number of these contributions is greater than or equal to the contribution threshold of the target problem type, the member is selected.

A simple solution would be to browse linearly the contribution traces of all members in order to detect those having a context similar to the target problem, and to calculate their number. This solution arises a problem related to the execution time. Indeed, in an environment dedicated to community problem solving, the number of comments and therefore the number of traces to be analysed, increase over time. Therefore, the execution time of the algorithms analyzing these contributions linearly will dramatically increase.

• 1)    To remedy this, we propose to do a preliminary treatment for limiting the number of traces to be analyzed before performing the traces analysis algorithm itself. Thus, we use two complementary algorithms: A filtering algorithm, which aims to eliminate some members from the list of the potential candidates to be selected, that we believe as not able to participate in solving the problem based on their previous contributions. We perform this analysis without browsing the traces files but based on indices that we call “indices of contribution” (section V.B.). This algorithm uses operations of search in a tree representing the indices of contribution, the number of contributions in this case does not affect the number of search operations.

• 2)    A traces analysis algorithm which consists in an optimal analysis of traces after filtering, based on the digital representation of these traces (section V.E.).

V.    Filtering and Traces Analysis

• A.    Context representation

We consider:

• •    C = {C1, C2, ..., Ci, ..., Cn}, the set of the context attributes of a problem, n is the total number of these attributes. This context represents both, the problem dimension and the domain profile dimension of the requesting member, as explained in section 4.2.

• •    Vi = {V i,1 ,V i,2 ,…,V i,mi }, the set of possible values for attribute Ci, mi is the total number of these values. For example, if we consider that the attribute Cx is representing the competence level of a member in a programming language, and that this attribute has 3 possible values (novice, intermediate and expert), the set Vx is as follows:

Vx = {1 (novice), 2 (intermediate), 3 (expert)}, with mx = 3

• •    Cxt(P) = {V 1,k1 ,V 2,k2 ,…,V i,ki ,…,V n,kn }, the context of the problem P represented by the values of the n attributes characterizing the context in which the problem P has been encountered, with V i,ki ∊  V i =

{V i,1 ,V i,2 ,…,V i,mi } and 1 ≤ ki ≤ mi.

• •    VR T = {R T,1 , R T,2 , …,R T,i ,…,R T,n }, the vector of

relevance of the type of problem T where R_T,i is the binary weight associated with the context attribute Ci for the type of problem T. R T,i =1 or R T,i =0 depending on the pertinence or not pertinence of Ci respectively.

• •    R_Cxt(P) = {V i,ki } / weight(Ci) = 1}, the relevant

context of the problem P which is a subset of the Cxt(P) represented only by the values of the relevant attributes for the type of P according to the relevance vector.

• •    R_Num_Cxt(P), a numerical representation of the relevant context of the problem P that will facilitate the processing of data by the selection algorithms. Indeed, when a non-numeric attribute Ci takes a value V_i, j , this value is replaced by the index j. The indices are then concatenated to represent the context as a number.

• B.    Contributions representation

As stated in section IV.D., we use contributions indices to enable the filtering algorithm to take decisions about eliminating some members from the list of potential candidates without having to browse their traces. The index of contribution is a value that characterizes the number of relevant past contributions of a member to solve problems of a given type in a given context.

Thus, we define for each member M, for each type of problem T: Ic M (T), as the total number of past relevant contributions of the member M to solve difficulties of type T.

We consider the contexts of two problems P1 and P2 as similar if they are of the same type and if the values of the relevant attributes that constitute the relevant contexts of the two problems R_Cxt(P1) and R_Cxt(P2) are similar.

We propose then, two similarity measures for the values of the context attributes:

• •    Absolute similarity: Two values are similar if they are identical.

• •    Relative similarity: A semantic similarity that characterizes the ability of solving problems according to the values of context attributes. We consider that a member having a high competence level can help a member with a lower level, while the reverse case is not true. To represent this, and considering the numerical representation of the context announced above, we consider two values as similar if the value of the target problem context is less than or equal to the value of the context of the past problem.

Consequently, for each value Vi,j of a context attribute Ci, we note IcM,T(Vi,j) the contribution indice of the member M, for the type of difficulties T, in a context where the value of the attribute Ci is similar to Vi,j. Here, the similarity depends on the attribute and may be absolute or relative.

Finally, we define for each member, for each type of difficulty and for each attribute of the context, the vector of contributions characterizing the number of relevant contributions of the member M for difficulties of type T in relation to all possible values of the attribute of context Ci:

Vc M,T (Ci)=(Ic M,T (Vi,1),..,Ic M,T (Vi,j),..,Ic M,T (Vi,m)).

Fig. 5 below shows graphically, an example of contributions tree of a member M.

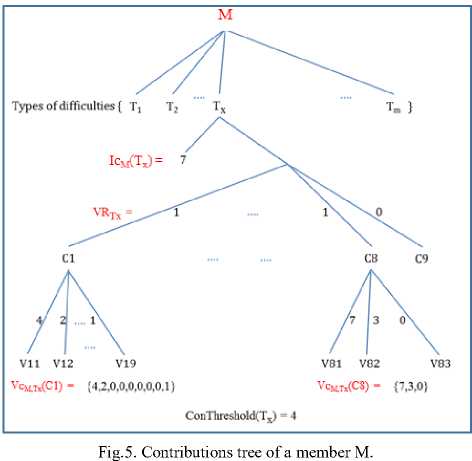
The member M has contributed in a relevant way, to solve 7 problems of type Tx (Ic M (Tx)=7). We also see that the member M has helped 3 other members having for the attribute C8, a value similar to V 8,2 =2 (intermediate) noted IcM,T(V_8,2)=3. The same member M has also helped 4 members having for the attribute C8, a similar value to V_8,1=1(novice), noted IcM,T(V_8,1)=7.

Finally, the vector of contributions characterizing the number of relevant contributions of the member M for the difficulties of type Tx related to all of the possible values of the attribute C8 is noted Vc M,T (C8 )= (7,3,0).

For proactivity and optimization of the response time, updating of the contribution indices of a member is performed implicitly at the time of declaration of a comment as relevant. Contribution indices of the member’s sub-tree related to the corresponding type of difficulty are updated then.

• C.    Traces representation

For a type of difficulty T, for a member M, we represent the traces of his contributions by a set of pairs: Trace=(R_Num_Cxt(P), Cont_Nb), where Cont_Nb is the number of times that this member has contributed pertinently to solve difficulties of type T in contexts identical or similar to R_Num_Cxt (P).

If we suppose that a member M has provided 3 pertinent contributions in resolving problems of the same type and in contexts identical to the context of the problem P: R_Num_Cxt(P) = 1322 , this trace is represented by the pair: Trace = (1322, 3) and numerically by the number 13223 .

• D.    Filtering algorithm

The filtering algorithm aims to identify, among the CoP members not selected by the static rules, a set of members judged not able to participate to the difficulty solving in order to remove them and therefore reduce the complexity of the traces analysis algorithm.

When a problem P of type T is published, characterized by a context R_Cxt(P), the filtering algorithm considers that a member M is not able to participate in solving P when:

• 1)    The number of his past contributions related to difficulties of type T is less than the contribution threshold of the type T. This is verified if Ic_M(T)

• 2)    The index of contributions of type T is higher than the contribution threshold but the number of contributions related to contexts similar to the context of the target difficulty is less than the contribution threshold of T. This is verified

if IcM(T) > ConThreshold(T) and if IcM(T) > ConThreshold(T) and if IcM,T(Vi,j) < ConThreshold(T) / Vi,j ∈ R_Cxt(D)

If we consider the contributions tree of the member M (Figure 5 above), and if we suppose that the aid requester is expert on the competence that attribute C8 represents (C8 = 3), then member M cannot help him since his index of contributions related to the value V8,3 is less than Contributions Threshold of T (IcM,T(V8,3)=0 < ConThreshold(T)=4).

As summary, at this stage of our members’ selection approach:

• •    A set of members are selected using a static selection.

• •    Among the not selected ones, a set of members are filtered by the filtering algorithm.

• •    The remaining members are subject to a traces analysis process that will be described in the following paragraph.

• E.    Traces analysis algorithm

The objective of traces analysis is to find, among the members not yet selected, who can help pertinently to solve the target difficulty.

Given the context of a target problem P of type T : R_Num_Ctxt(P), the traces analysis algorithm browses the traces of all non-selected members for the type of problem T. The algorithm decides then to select a member when the number of his contributions in similar contexts to R_Num_Cxt(P) is greater than or equal to ConThreshold(T).

Thus, given the R_Num_Cxt(P) of a target problem P, the traces analysis algorithm browses the traces file of a member using the dichotomic search (since the lines are sorted) in order to identify the position where there is a trace having the same or the closest representation to R_Num_Cxt (P) of the target problem.

At the end, the traces analysis algorithm calculates the sum of contributions in contexts similar to the context of the target problem in order to decide (or not) to select the member, depending on the contribution threshold of the target type of problem.

VI.    Experiments

• A.    Objective

First of all, we have tested NICOLAT system within a real CoP of members interacting about a specific domain. The CoP members are professors from the Faculty of Sciences and Technology of Fez in Morocco: 30 professors using a pedagogical method called MAETIC (French acronym: Méthode pedAgogique instrumEntee par les Technologies de l'information et de la Communication) [32]. The domain of the CoP here is the problems encountered by the users of the method while implementing their pedagogical devices. Indeed, while the teachers are using MAETIC in classroom they may experience problems. They then interact through NICOLAT system to try to solve them.

With the objective to validate our selection approach, we propose to evaluate its advantages according to several aspects:

• •    The gain in using filtering before the analysis of traces.

• •    The gain related to the proposed organization of the traces files (numerical representations of the relevant contexts and sorting of the representations in traces files).

• •    The gain in terms of execution time of the filtering and trace-analysis algorithms for different types of problems, and different sizes of the CoP.

The experiment on the real CoP cited above is not able to validate the three aspects of the selection approach. Indeed, the CoP members had very close specialties and are considered, in 90%, as novice in MAETIC (domain of the CoP). So, they are not representative for validating our selection approach. We then simulated a CoP of 30 teachers, with diverse profiles in terms of specialization, expertise in MAETIC and level of activity in the CoP. We have 45% of novices, 30% of intermediate and 25% of expert members in MAETIC. The percentage values in the distribution of simulated members on these three categories is based on the work of Wenger [25]. A novice, in our simulated CoP, has a number of relevant contributions between 6 and 20, an intermediate between 21 and 40, an expert from 41 to 60.

• B.    Gain in terms of quality of selection

We followed the process of selecting members, step by step, in order to analyze the gain of each stage of the static and dynamic selection. A classification of major MAETIC difficulties encountered by the users has been elaborated [30]. We simulated 8 types of these problems encountered in real environment, each one with its own relevance vector VR(T).

The table 1 below, shows the following collected values:

• •    A: The number of members selected by the static selection.

• •    B: The number of members eliminated by the filtering algorithm.

• •    C: The number of members whose traces will be analyzed by the traces analysis algorithm, with C=30 (size of the CoP) – 1 (the aid requester) – A – B.

• •   D: The number of members selected by the

dynamic selection (after the traces analysis).

• •    E: The total number of selected members, with

E=A + D.

• •    F: The total number of eliminated members, with

F= 30 – 1 – E.

The last column represents the gain related to the filtering algorithm that we define as the number of members who have been eliminated by the filtering algorithm divided by the total number of eliminated members (Gain = B/F). Indeed, this number shows the performance of the filtering algorithm and its ability to minimize the processing of traces analysis algorithm (the next stage of dynamic selection). We represent the gain also in terms of percentage.

Table 1. Percentage gain

	VR(T)	A	B	C	D	E	F	Filtering gain
T1	101001100	4	17	8	5	9	20	17/20	85,00%
T2	000111110	2	13	14	3	5	24	13/24	54,17%
T3	100001110	7	9	13	7	14	15	13/15	86,67%
T4	000001110	2	9	18	15	17	12	9/12	75,00%
T5	100001100	0	15	14	5	5	24	15/24	62,50%
T6	001001100	0	14	15	3	3	26	14/26	53,85%
T7	100101110	2	13	14	2	4	25	13/25	52,00%
T8	000001101	6	11	12	7	13	16	11/16	68,75%

In all of these cases, we find first, that E is always greater than A for all types of problems. That is to say that the total number of the selected members is always greater than the number of those selected statically. This shows the relevance of our dynamic selection that completes the list of selected members theoretically based on their profiles, by really active members in the CoP based on their relevant contributions in the past. On the other hand, we find that the gain of the filtering algorithm varies between 52% and 85%. That is to say, it allows to filter between 52% and 85% of the members that should not be selected and thus minimizes the processing of the traces analysis algorithm by the same percentage.

• C.    Gain in terms of execution time

In order to demonstrate the added value of each step of our approach, we measured the execution time of the filtering and the traces analysis algorithms in different cases:

• •    Case 1: Dynamic selection without prior filtering and sorting of numerical representations of the traces. The execution time is denoted in this case: T(-F-S).

• •    Case 2: Dynamic selection with filtering but without sorting the traces files. The corresponding execution time is denoted in this case: T(+F-S).

• •    Case 3: Dynamic selection with filtering and sorting the traces files. The corresponding execution time is denoted: T(+F+S).

We made the calculations for the 8 types of problems considered in the first experiment. In addition, and in order to check the scaling properties, we conducted the experiment for different sizes of the CoP ranging from 30 to 5000 members. We have run our tests on a Windows 7 64-bit desktop computer, with an Intel (R) Core (TM) i7-3770 @ 3.40 GHz CPU and 32 Gb of RAM.

Table 2 below presents, for the type of problem T1, the considered CoP sizes, the execution time corresponding to the three above cases as well as the obtained gains.

Table 2. Results related to a problem of type T1

CoP Dimension	30	50	100	500	1000	5000
	Execution time in ms
T(-F-S)	27	42	61	127	223	5376
T(+F-S)	15	22	40	92	137	588
T(+F+S)	8	11	22	68	86	228
	Gain in %
Filtering Gain	44,44 %	47,62 %	34,43 %	27,56 %	38,57 %	89,06 %
Sorting Gain	46,67 %	50,00 %	45,00 %	26,09 %	37,23 %	61,22 %
Global Gain	70,37 %	73,81 %	63,93 %	46,46 %	61,43 %	95,76 %

Considering only the first column of the table, representing the initial CoP size of 30 members, we observe many successive minimizations of the execution time while integrating the different algorithms:

• 1)    The execution time corresponding to the dynamic selection without filtering and with unsorted traces files is T(-F-S) = 27ms.

• 2)    Adding the filtering step, the execution time

passes to T(+F-S) = 15ms, which corresponds to an improvement of 44.44%.

• 3)    Adding the traces sorting, the execution time passes to T(+F+S) = 8ms, corresponding to an additional improvement of 46.67%.

• 4)    A total improvement of 70.37% compared with dynamic selection without filtering and sorting.

Considering the variation of the CoP number of members, and for the 8 types of problems (Fig. 6), we notice that the obtained gain does not depend on the types of problems since it converges to values between 70% and 95% for the largest CoPs.

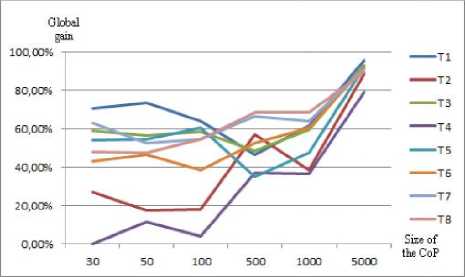
Fig.6. Global gain in function of the types of problems and CoP sizes

VII. Conclusion

In this paper, we focused on a dynamic members selection approach proposed in the frame of a system support of CoPs, called NICOLAT. Learning through CoPs is mainly a problem-based learning, where members interact between them to help each other resolve the problems they may encounter relatively to the shared practice of the CoP.

In our approach, we took into consideration the dynamicity of the members’ level of expertise in the domain of the CoP. This latter is considered in growth when the number of past contributions of a member increases over time. Given a new problem, our selection approach tries to select a set of the most active members in the past to resolve similar problems in similar contexts. They are considered as the most appropriate to provide a positive contribution to the target problem at a given time.

Our NICOLAT system is currently in use by a CoP of teachers. Before integrating the dynamic selection functionality in the real environment, we proceeded to its validation by simulation. The preliminary results seem to be satisfactory. Our perspective is to experiment the dynamic selection approach in a real environment and for a large CoP.