Fast x-ray sum calculation algorithm for computed tomography problem

Computed tomography (CT) is a measuring and computing method to estimate the internal structure of a three-dimensional object according to the results of X-ray penetration through the object. Today, CT is one of the most powerful methods of nondestructive testing. CT is most commonly used in medical diagnostics [1–3]; however, CT is also used in industry to detect hidden defects and to control the quality of assembly [4], in geology to study rock characteristics [5, 6], in archeology and paleontology to study the internal structure of petrified objects [7], etc.

The core of the CT method is to estimate a spatial distribution of an X-ray attenuation coefficient in the object according to the set of projections measured at successive X-ray probing at various angles. In this case, probing can be made with parallel or cone X-ray beans; using either monochromatic or polychromatic radiation. According to the abovementioned factors, CT data pre-processing methods are changed, as well as numerical methods of the reconstruction itself. The most popular group of reconstruction methods includes integral approaches, the mathematical tools of which are based on the property of invertibility of Radon transformation. The classical methods of this group include the filtered back projection method and the Fourier synthesis method [8–10]. The methods of the second group are based on the application of algebraic approaches. In this case, the CT problem is reduced to the iterative solution of the given algebraic equation [11–14], where each voxel of the reconstructed image is considered as an independent variable. Probabilistic and statistical approaches are included into a separate group of methods.

An important feature of algebraic methods is a possibility to work particularly with a highly noisy and/or fragmentary data, e.g., received during scanning an object at a small number of angles [15–17]. Development of algorithms working under such conditions is especially urgent due to the necessity to decrease scanning time. Decrease in registration time leads to decrease in the radiation dose received by the patient during a medical examination, as well as increase in the reconstruction accuracy with time resolution (the so-called “4D tomography” [18]).

However, algebraic methods of reconstruction are weaker than integral methods with regards to the speed of image reconstruction, their asymptotical complexity worsens as the reconstructed image resolution increases. The latter fact becomes more important due to the fast growth of resolution enhancement of measuring equipment. Nowadays, the efforts to improve the operation time of algebraic methods are developed in two different directions. First, expand simultaneously used computation capacities with features for parallelism (e.g. [19]). Second develop new reconstruction algorithms having a lower computation complexity (e.g. [20]).

In iterative methods of computed tomography, each iteration requires to calculate the so-called ray sums, which are the sums of values of the current reconstruction approximation for a set of lines, corresponding to a measurement scheme in use. In cone-beam tomography in order to reconstruct an image of the linear size n, a total of 0(n3) ray sums is calculated at each iteration. Note that a set of lines for which the calculation is performed can be changed depending on the operation mode of the device, but asymptotics of the power of the set is not changed. The direct calculation of such ray sums requires 0(n4) summations. This fact limits the performance of the iterative methods and prevents their wide propagation. A novel algorithm proposed in this paper performs calculation of these sums using only 0(n3 л/n) summations. The algorithm is based on the following two ideas. First, we replace of discrete lines with dyadic patterns. Second, we use Method of Four Russians to balance precalculation and direct recalculation. The Ershov algorithm for dyadic patterns [21] allows to simultaneously sum the values along 0(n4) dyadic patterns in a three-dimensional image with a n side using 0(n4) summations. The algorithm [21] is a generalization of the fast Hough transform algorithm, which is used in various computer vision problems [22]. Some mentions on the existence of such computational scheme were made in the earlier work by Donoho and Levi [23]. However, the algorithm itself was presented and described for the first time in [21]. This work also shows that dyadic patterns are deviated from a geometric prototype for not more than -^62 log2 n in the worst case, which is quite acceptable for tomographic images, where n rarely surpasses 4096. But, unfortunately, the Ershov algorithm does not allow to get a faster response if the number of the required sums decreases. Therefore, the application of the Ershov algorithm gives the same asymptotic complexity as direct calculation. In this paper, we propose an algorithm, which is the result of applying the so-called Method of Four Russians to the Ershov algorithm. The Method of Four Russians [24] was introduced in 1970 by V.L. Arlazarov, E.A. Dinic, M.A. Kronrod, and I.A. Faradjev for the problem of multiplication of boolean matrices, and for its equivalent problem of finding the transitive closure of a graph. The main idea of the method is to split the matrices into strips for which the multiplication is performed using consructed lookup tables, and the width of the strips is determined by adjusting the lookup table construction complexity with the complexity of calculating the final multiplication result. The same idea of separation and adjustment of the precalculation and the inference parts of the algorithm will be used in this paper. We show that if the Ershov algorithm is stopped at the k-th iteration, where k = log2 s/n, then such precalculation requires 0(n3 л/n) summations whereupon every line can be summed using the sums already calculated for sections by n operations. Therefore the total complexity is 0(n3л/n) for 0(n3) straight lines.

The paper is organized as follows. Section 1 describes mathematical background of the computer tomography problem. We give series of steps, which, in case of a monochromatic probing, linearizes the problem, i.e. allows a transition from the measured values to the ray sums. Next, for a polychromatic probing, the notion of an average X-ray attenuation coefficient is introduced; the paper shows that in the case of a definite approximation of tomographic projection formation model the reconstruction problem can also be made linear. Section 2 presents a fast X-ray sum calculation algorithm when discrete lines are replaced with dyadic patterns. We describe the Ershov algorithm, which does not allow to decrease the computational complexity of direct calculation of 0(n ⁴ ), if 0(n ³ ) ray sums are calculated. Next,we propose a new algorithm, which allows to decrease the total complexity from 0(n ⁴ ) to 0(n ³ л/n) when calculating 0(n ³ ) ray sums.

1.    Mathematical Background of the Computer Tomography Problem

If a parallel scheme (Fig. 1) is implemented to collect tomographic projections, then reconstruction can be performed layerwise. Let us focus on the parallel scheme and define the problem of tomography on a plane. Consider a fine X-ray beam of the photon energy E passing through the section of a generally non-homogeneous object and attenuated in this path (Fig. 1). Suppose that the X-ray beam is registered by the ideal detector, i.e., the value of the registered signal is exactly equal to the number of photons reaching the detector. In this case we ignore the scattering process and the secondary re-radiation processes. The structure of the object is given by a spatial distribution of the linear attenuation coefficient ^(x, y), which describes the object capability to attenuate the X-ray energy radiation E . If I 0 is the intensity of the induced beam, then the value of the registered signal I is calculated according to the Bouguer–Lambert–Beer law:

∞

I(p, ф) = I 0 exp — / д (p cos ф — l sin ф, p sin ф + l cos ф) dl

-∞ where (p, ф) are normal coordinates of the registered beam, and the absorption outside the object is considered to be zero.

The problem of computer tomography is to reconstruct the spatial distribution of the linear X-ray attenuation coefficient based on a set of projections registered with certain resolution and at various angles. By the ray sum S we mean an integral of the attenuation coefficient for the probing direction. Write the expression that connects the value of the ray sums and the value of the signal I :

S ⁽p,^ф) = In I ⁰

I (p,ф)

∞

J ц (p cos ф — l sin ф, p sin ф + l cos ф) dl.

-∞

The further situation is complicated if polychromatic radiation is used for probing. In commercial medical and industrial tomographic scanners, a broadband spectrum is used. The linear X-ray attenuation coefficient depends on energy. It means that if radiation is polychromatic, then various components of radiation are not similarly attenuated by the object. Besides, the detectors of most tomographic scanners are not energy-dispersive, i.e., the detectors register an integral signal, and the distribution of radiation in quantum energy seems to be lost. In this model, the expression,

X-ray

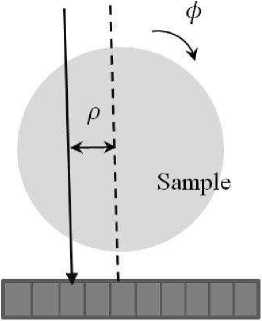
Position sensitive detector

^whi^ch i^nterco^{nnects t}h^{e va}l^ue of ^th^e Fig. 1 . Schematic diagram of formation of ^regi^stered ^sig^nal ^and ^th^e di^strib^utioⁿ of tomographic projection in a parallel circuit the attenuation coefficient, is changed as follows:

∞

I W) = I

I o (E ) exp

∞ ц (p cos ф — l sin ф, p sin ф + l cos ф, E) dl x(E)dE,

-∞

where x(E) is the detector sensitivity to quanta with the energy E .

If the dependence of absorption on the quantum energy during reconstruction is ignored, then cupping artifacts appear in the reconstructed image [25]. There exist several approaches to solve this problem, including processing of the reconstructed images [26]. Attempts to create mathematically correct reconstruction methods for the polychromatic mode seem to be more interesting. Therefore, the paper [27] shows that, in approximation of the only material of the object, there is measured data mapping, which allows to use linear reconstruction methods and to obtain the results which are not corrupted by artifacts. Efforts were taken to create methods of multicomponent reconstruction [28], which can be used when the object contains two types of areas differing in composition. In this case, the reconstruction problem is solved in relation to weight fractions of chemical elements comprising the sample while the main model still remains linear.

If the function S(p, ф) is known in all points, then the tomography problem is solely reduced to the problem of conversion of Radon transformation. The filtered back projection method implements the operation of conversion of Radon transformation for the finite number of measurements S and gives good results if the number of projection angles coincides with the order number of linear dimension of the restored image, and the measurements are equally spaced for both ρ, and φ, with the projection angles covering the whole circumference. There is no such simple and accurate integral method for a cone-beam scheme; instead, approximation integral methods, such as the Feldkamp method, are used. In medical applications, the case of a small number of angles is of special interest due to a limited radiation burden. It is turn while in non-destructive examinations of long length objects. The case of a limited angular range is of interest. In all the above-mentioned cases, an algebraic approach does not require any modification, since the approach reduces the tomography problem (in the two-dimensional case) to the solution of the following linear equation system:

{ Е

( x,y ) ^L ( P i ,Ф i )

Ц ^{( х,}У) = S ⁽P i ,M

where L(p, ф) is a set of pixels of the reconstructed image, which approximates the straight line with the normal coordinates (p, ф). In a cone-beam scheme, the system is written in a similar way. In the algebraic approach, the function µ is defined iteratively; i.e., multiple calculation of ray sums with reference to the current approximation of µ is required. Next, we show how this operation can be speeded up by an algorithm in a general case.

2.    Fast Algorithm of Simultaneous Calculation of a Large Number of Ray Sums in the Three-Dimensional Case

Discrete straight line approximation on a plane can be performed by several methods. Let us refer to the | t | <  1 lines as of the type y = ntx y + s preferentially horizontal, and refer to the other lines as preferentially vertical. If discretization for the first type is implemented, then discretization for the second type can be obtained by conjugation. The most popular way is the method when every column of the image of a preferentially horizontal line includes the matching pixel which is the nearest one from this column (considering a roundoff). Such discrete lines are often erroneously called Bresenham’s lines after the author of the famous computer graphics algorithm that does not use multiplication. In 1992, P. Brady introduces another recursive discretization method for n = 2 ^p , where p is an integer. The method is sometimes called approximation with a dyadic pattern [21].

Patterns of this type are characterized by a large number of form coincident line segments having different slope angles. For example, patterns beginning in the same point and having the slope t, which differs by one, coincide at the half-length (see Fig. 2). The use of memorization of general sub-sums and elimination of doubling calculations allow summing up the image along all possible preferentially horizontal dyadic patterns from t >  0 for n ² log ₂ n summations. In general, for all dyadic lines, the number of operations is 4 times larger.

Among other things, the paper [21] proposes a similar algorithm for lines in the threedimensional space. In order to construct the algorithm, the lines are divided into three types. Each type is attributed to one of the rectangular coordinate system axes with which the line has the smallest angle (Fig. 3). Let us consider the lines which are preferentially directed along the vertical axis z3. Such a line can be uniquely given by the points (s1, s2, 0) and (s1 + ti,s2 + t2,n — 1) that belong to the opposite sides of the cube. Depending on the signs of the parameters t1 and t2 determined with reference to the axes of the horizontal plane, the lines of the same type are divided into four subtypes. Fig. 3 shows the example, when both signs are positive, i.e. the line belongs to the III-th subtype. Note that dyadic patterns approximate the lines with an error increasing with n. In [21], it is shown that for the value -^2 log2 n, the upper limit belong to the maximum deviation of a three-dimensional dyadic pattern from the geometrically exact line. For n = 4096, it makes only 2^/2 of the voxel. Moreover, though the worst absolute coordinate error of such approximation increases with n, the worst relative coordinate error quickly decreases.

For the lines of the same type, the Ershov algorithm requires less than 2n 4 summations, therefore the total number of the lines with integral values of the parameters (s 1 ,s ₂ ,t 1 , t ₂ ) is estimated as 24n ⁴ summations. It is unexpectedly good result, since each of the lines effectively requires only 2 summations irrespective of the length though such result fails to speed up ray sum computation because the naive algorithm has the same complexity. This is because the Ershov algorithm basically calculates sums along all the lines rather the required lines only. We show how the Ershov algorithm may be modified considering the fact that algebraic reconstruction algorithms require calculation of 0(n ³ ) rather than 0(n ⁴ ) sums.

Consider separate iterations of the algorithm described in [21]. Initially, the original three-dimensional image having the size n x n x n includes sums for all possible dyadic patterns having the length 1 (i.e., all separate voxels of the three-dimensional image). Next, at every i-th step of the algorithm, where i E { 1,2,...,k } , we calculate the sums considering the dyadic patterns of the length L = 2 i , with the complexity of the i-th step equal to 0(n ³ • 2 i ). After the k-th step, where k = log ₂ n, we calculate the

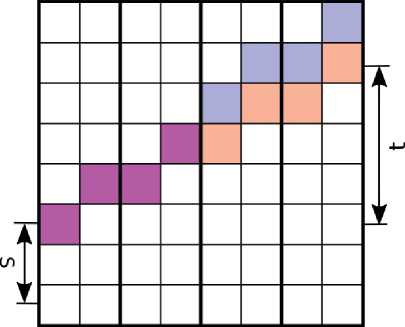
Fig. 2 . Two dyadic patterns in a twodimensional space with slopes differing by one

t2

s2

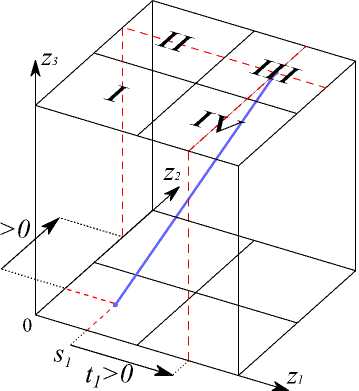
Fig. 3 . Parameterization and typification of dyadic lines in the three-dimensional space

sums for all the dyadic patterns of the length n, and the algorithm stops (see. Fig. 4).

The complexity of all the steps of the algorithm is as follows:

0(n3 • 20) + 0(n3 • 21) + 0(n3 • 22) + ... + 0(n3 • 2log2n) = 0(n3 • 2log2n) = 0(n4), which is not better than the direct calculation of the required 0(n3) X-ray sums.

Nevertheless, let us consider the modification of the algorithm which stops calculation at the x-th step, where x < log ₂ n whereupon the required 0(n ³ ) ray sums are additionally

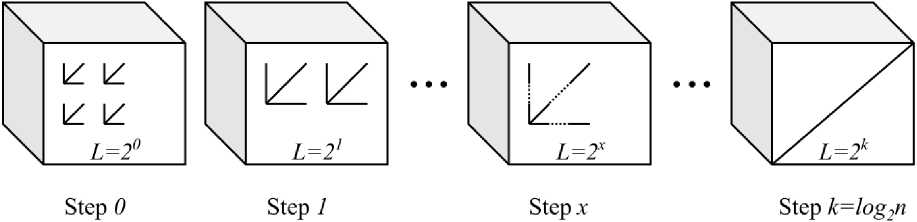
Fig. 4. Logical representation of steps to expand the Ershov algorithm calculated using the obtained sums against the dyadic patterns having the length 2x. In this case, the complexity of the calculation of every sum is 0(n) = 0(2log2n-x). Now, we apply the complexity precalculation and recalculation adjustment principle which is similar to that implemented in the algorithm of Four Russians to search for optimal division of the matrix, i.e., we find step index x at which the total complexity of calculation for steps 0,1,..., x of the algorithm [21] and the complexity of calculation of the required ray sums coincide:

0(n 3 • 2 0 ) + 0(n 3 • 2 1 ) + ... + 0(n 3 • 2 x ) = 0(n 3 • 2 ^log 2 n-x ),

0(n 3 • 2 x ) = 0(n 3 • 2 ^log 2 ^{n - x} ) ^ x = 2 log ₂ n = log ₂ V n.

For the optimal x = log ₂ Vn, the total complexity of calculation 0(n 3 ) of the required ray sums is as follows:

0(n 3 • 2 ^log 2 V n ) = 0(n 3 V n).

Conclusion

The important advantage of algebraic methods of tomographic reconstruction is their ability to work with very noisy and/or incomplete data, which is important when radiation dose limitations are imposed. In this case a disadvantage of the algebraic methods is their high calculational complexity. The novel ray sum calculation algorithm presented in this paper allows to decrease the time for one iteration of an algebraic method to 0(n 3 Vn), where n is a linear size of the reconstructed image. This result was achieved owing to application of the Method of Four Russians developed by V.L. Arlazarov, E.A. Dinic, M.A. Kronrod and I.A. Faradjev to the Ershov algorithm. Taking into account that the constant associated with the complexity of the described algorithm is close to one, and considering a reconstructed image of size n = 4096, we can obtain roughly 64 iterations of an algebraic method for the same time as the most popular integral reconstruction method, Feldkamp algorithm, which has a complexity of 0(n ⁴ ). Thus, it can be considered a breakthrough in the performance of algebraic tomography methods. Note that this advantage is accompanied by the increase in the requirements to RAM from 0(n ³ ) to 0(n 3 Vn) to store the precalculated sums. Decreasing these requirements could significantly expand the applicability of the new algorithm in practice; it is an apparent direction for further studies.

Acknowledgment. This work was partially financially supported by the Russian Foundation for Basic Research, projects 18-29-26020 and 18-29-26027.