Флуктуации интенсивности сигнала в атмосферных оптических системах передачи информации

Развитие лазерных систем передачи информации потребовало изучения различных аспектов влияния турбулентной атмосферы на характеристики распространяющегося оптического излучения. Подробный обзор теоретических и экспериментальных исследований по этому вопросу приведен в [1], причем особое внимание обращено на установление статистических характеристик флуктуаций интенсивности принимаемого сигнала.

Знание вида функции распределения плотности вероятностей флуктуаций (ФРПВФ), являющейся наиболее полной статистической характеристикой случайного процесса, необходимо при определении вероятности ошибки и надежности работы оптических линий связи, расчете уровня помех в лидарных системах и т. п. [2].

К настоящему времени установлено, что вид ФРПВФ зависит от величины универсального безразмерного параметра в 2 , представляющего собой дисперсию логарифма флуктуаций амплитуды плоской оптической волны, вычисленную в приближении метода плавных возмущений:

Р 0 = 1,23 С П к ^7/6 L ^11/6, (1) где C ² _n – структурная характеристика показателя преломления воздуха, отражающая степень турбулентных возмущений; k = 2п / X — волновое число; X — длина волны; L — длина трассы в турбулентной атмосфере.

Условно все встречающиеся на практике ситуации при любой комбинации величин, входя-

щих в соотношение (1), подразделяются на три случая флуктуаций интенсивности: Р 0 ^ 1 — слабые, Р 0 = 1 - насыщенные, Р 2 » 1 — сильные флуктуации.

В области слабых флуктуаций теоретические работы, подкрепленные экспериментальными данными, однозначно указывают на логарифмически нормальную ФРПВФ интенсивности сигнала:

^рл . н ( I c ) =     ',, exp

I c а с V2n

I_c >  0

где а с и т с - соответственно дисперсия среднего значения и среднее значение интенсивности, связь между а с и дисперсией интенсивности следующая:

а2 = ln (а2 + 1), где а2 = (IIc - mc)^2 / m2, « (...) » означает статистическое усреднение по ансамблю событий.

Для технических приложений (связь, локация и т. п.) область насыщенных и сильных флуктуаций представляют значительный интерес, поскольку длина трассы обычно велика и поле в месте приема – суперпозиция многих рассеянных полей. В этих областях вопрос определения вида ФРПВФ достаточно сложен.

Логарифмически нормальная ФРПВФ предсказывает неограниченный рост флуктуаций интенсивности с ростом в 2 , но этого, как показывают эксперименты, не происходит. В области

-

( ln ¹с

-

2а

тс )

с

,

слабых флуктуаций для плоской волны ст2 = Р2 по мере увеличения в2 вначале наступает явление насыщения флуктуаций, при котором ст2 * Р2, а далее последующий рост в0 приводит к плавному уменьшению ст2. Если считать, что в области сильных флуктуаций поля рассеянных волн статистически независимы, то использование центральной предельной теоремы приводит к односторонней экспоненциальной ФРПВФ суммарной интенсивности

Рэ ( I c ) = —exp |-- I c - |, I c > 0. (3) m c I m c J

Для области же насыщенных флуктуаций те- оретическим путем получено несколько видов ФРПВФ [1]. Одним из главных условий применимости подобных распределений является их переход в случае увеличения параметра Р2 в экспоненциальное распределение. Этому условию отвечает широко используемое K-распределение

Световой фон для оптических систем является аддитивной помехой [4]. Обычно для учета влияния фоновых помех используют модель равномерно излучающих (ламбертовских) источников, подразделяемых на диффузно распределенные и дискретные. К первому типу относятся небесные источники фонового излучения, занимающие полностью полусферу небесного свода. Их излучение постоянно поступает в приемную оптическую антенну, тогда как более сильное излучение дискретных источников (Солнце, звезды и т. п.) попадает в антенну в зависимости от ее ориентации и может быть до некоторой степени или полностью устранено. Таким образом, основной вклад в помехи вносят диффузное излучение, в котором наиболее значительны рассеянное солнечное излучение (РСИ), тепловое излучение, а также свечение атмосферы, причем для волн с X < 3 мкм преобладает РСИ, для волн с X > 4 мкм — тепловое излучение, флук-

2 а ^{а 1}         / /----\

P K ( I c ) =        ( ^а I c ) 2 K а-1 ( ² Ja I c ) ,

1 (а)

туации интенсивности которого распределены

нормально:

Ic > 0, где Kа—1(-) — функция Макдональда; а — число рассеивателей; Г (а) — гамма-функция.

Распределение (4) нормировано относительно среднего значения флуктуаций интенсивности,

P (IФ )=

G ф д/2Л

exp

( ^IФ ^{- т}Ф ) 2 2ст ф

^Iф > ⁰,

принятого за единицу.

Хотя при I c ^м Pk ( I c ) ^ exp ( - I c ) , но для в о < 1 Pk ( I c ) не переходит в логарифмически нормальное распределение и, следовательно, имеет ограниченный диапазон применения. Подобные недостатки присущи и другим распределениям, применяемым в области насыщения.

Неоднозначность теоретических ФРПВФ потребовала проведения экспериментальных исследований, которые также приводят к противоречивым результатам. На наш взгляд, есть ряд причин для объяснения этого факта, и, в частности, одной из основных является практически постоянное наличие в атмосфере флуктуаций интенсивности светового фона, которые при значительной длине трассы могут быть сопоставимы с флуктуациями интенсивности слабого

где т ф и ст ф — среднее значение и дисперсия интенсивности фона соответственно.

Для РСИ можно выделить два случая:

а) если рассеяние солнечного излучения осуществляется облаками, то для флуктуации интенсивности РСИ справедливо экспоненциальное распределение:

P ( 1 ф ) -

exp m ф

'— ф - 1

I ^тф J

^IФ > 0;

б) если в атмосфере преобладают молекулярное и аэрозольное рассеяния, то флуктуации РСИ подчиняются релеевскому распределению:

P ^{( I}Ф ^{) = ф} exp ^ст ф

2 I ф ^{2 ст} ф

^IФ >^0.

сигнала.

В связи с этим в настоящей работе исследуется влияние флуктуаций интенсивности естественного светового фона на ФРПВФ сигнала. Детальный обзор фоновых помех в окнах прозрачности атмосферы содержится в [3].

Кроме излучения небосвода имеется и разнообразное фоновое излучение от различных земных поверхностей и объектов, которое здесь не рассматривается.

Получим для наиболее распространенных ситуаций ФПРВФ суммы принимаемого сигнала и помехи, учитывая их независимость. В общем виде свертка или композиция двух функций распределения для случайных величин x и y будет

го

P i ( z ) = J P ( x ) P ( z - x ) dx ,                    (8)

-® где z = x + y.

Рассмотрим вначале область насыщенных флуктуаций, конкретизируя в распределении (4) параметр а. В [5] на основе экспериментальных данных показано, что в этой области зна- 22

чения о i лежат в диапазоне 2 <  g i < 3, и, так как связь между g | и а определяется соотношением

° I = 1 + а ’ то 1 < а < 2 , поэтому выбираем а = 1,5.

Используя для флуктуации фона наиболее часто встречающееся распределение (6) и нормируя его так же, как (4), получим для композиции флуктуаций сигнала и фона:

^< z ) = Т(Г5)(1'5Г X z                                                       (9)

X J 7_; ² K 0,5 ( 2715 7 ) exp [- ( z - 1 ф ) ] Д1 ф , 0

где z = 7 с + 7 ф .

Функция Макдональда при а = 0,5 сводится к элементарным функциям [6]:

K 0,5 ( Cx ) =

• 1      /   z ) _

=----exp I--I exp

• ²    m c    V m c J

x exp

где

Выполнив в (9) преобразование и интегрирова-

ние, получим:

P i ( z ) = 0,24п exp ( - z )

Г 6 z + 3 )       Г 3 I erfi I —=— I - erfi I I

V V6 J       V2J

где erfi – функция, связанная с интегралом ошибок.

Более актуальным является случай в 0 » 1, например, на протяженной трассе, когда флуктуации интенсивности фона могут даже превосходить флуктуации сигнала.

Для этого случая рассмотрим два варианта флуктуаций интенсивности фона – распределения (5) и (6), тогда как флуктуации интенсивности сигнала в обоих случаях положим подчиняющимися распределению (3).

Соответственно получим композиции сумм интенсивностей:

P ⁱ⁽ z )   о _ф 727 mc ^Х

z x J exp

( ⁷Ф ^{- т}Ф ) 2 ^{2 о} Ф

exp

(z - 7ф ) mc

dI ф =

U

Й7

( 2° Ф ) 2

U = ^тФ ⁺ mr

erf

² тф_ V 2° Ф J

I

z + U

V^{2 0} Ф J

erf ( x ) =

Ф ( x ) — интеграл ошибок и

P i ( z ) =

1                 I I= I exp I — | exp тстФ 0   V me J

( A

erf

U

V ²° Ф J

n

-у ^{ф ( x} ) ,

^{( z -} I c ) m ф

dI_c =

mс

^{- т}Ф

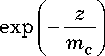
1-

exp exp

Полученные распределения отличаются от теоретических; в частности, распределение (10) представляет известный обобщенный закон Эрланга второго порядка, которое, если положить т Ф = 0, вновь переходит в экспоненциальное распределение.

Рассмотрим на примере распределения (10) влияние интенсивности фона на вид распределения. Для этого пронормируем это распределение на экспоненциальное ( т Ф = 0). Расчетные данные представлены в таблице.

Из данных таблицы следует, что форма кривой распределения остается постоянной при т Ф = 0,1 т с для любого отношения z / т с , меняется только среднее значение интенсивности. Отклонения от вида распределения начинают возникать при т Ф > 0,3 т с .

В экспериментальной работе [7] учет флуктуаций фона был выполнен аппаратурными методами. В результате при Р 0 = 9 была получена логарифмически нормальная ФРПВФ, что отличается от предполагавшейся теоретически функции.

Таблица

	1	2	3	5	10
0,1	1,1	1,1	1,1	1,1	1,1
0,3	1,14	1,41	1,41	1,41	1,41
0,5	1,28	1,74	2	2	2

Таким образом, полученные в работе результаты указывают на необходимость учета флуктуаций фона при проведении экспериментальных исследований.