Графы работ для представления некоторых задач математической физики

В связи с нарастающим многообразием и сложностью знаний становится актуальным создание сетевых библиотек моделей. В [1–4] изложены концепция и архитектура сетевой библиотеки Нива вычислимых математических моделей, результаты которых получают вычислениями на удаленном компьютере. К таким моделям можно отнести, например, имитационные модели.

В сетевой библиотеке модель представляется набором сценариев ее расчета. Сценарий для расчета модели на удаленном компьютере сетевой пользователь самостоятельно конструирует на своем компьютере в виде графа работ модельных компонент. Важно отметить, что сетевой пользователь оперирует здесь не отдельными математическими соотношениями модели, которые он зачастую недостаточно хорошо понимает, а оперирует заранее проверенными модельными компонентами. Таким образом, сетевая библиотека ориентирована на сетевого пользователя, а не на традиционную разработку моделей.

Библиотека не передает пользователю код модели. С согласия автора библиотека может предоставлять пользователю текстовое описание модели. Это позволяет сохранять авторские права.

Удаленный компьютер называется сервером. Сервер рассчитывает сценарий и результаты пересылает пользователю.

Представление задач графами работ хорошо известно и используется в программировании [5]. Представляет интерес исследование вида графов работ, которые могут быть использованы для представления характерных вычислительных задач моделирования.

1.    Графы работ и компоненты

Компонентой M={F,D} вычислимой модели называется исполняемый компьютером программный код, который реализует некоторую функцию F без параметров и исполняет ее над набором D специфических данных, называемых далее слотами. Компоненты, имеющие одни и те же F и D, но отличающиеся значениями данных из D, назовем МодОбъектами. Композицию МодОбъектов, представленных узлами в графе работ, назовем сценарием использования модели. Совокупность сценариев использования одной модели будем называть ГиперМоделью.

Каждому МодОбъекту приписывается содержательное имя вида [m][d], где m - имя для обозначения функциональности F компоненты M={F,D}, а d - имя набора значений слотов D этой компоненты. Мо-дОбъекты вместе с данными их слотов сохраняются в базе данных сервера. Имена [m][d] используются для поиска МодОбъектов в базе данных и в графе работ. На графе можно не указывать [d], если компонента имеет только один МодОбъект. МодОбъекты изображаются пиктограммами, размещенными в узлах графа. Если МодОбъект реализует элементарную операцию, например «+» или «-», в его изображение включен треугольник, а [m] совпадает с именем операции.

Сценарий визуально (мышкой) конструируется пользователем в виде графа работ. Сценарий рассчитывается удаленным сервером после ввода пользователем своих данных в компоненты и проверки сервером правильности графа. Результаты расчета сервер посылает пользователю на его компьютер.

Таким образом, модели в сетевой библиотеке представляются семействами допустимых сценариев - графов работ модельных компонент. Каждое семейство допустимых графов имеет формальное описание, хранимое в библиотеке, в котором допустимые компоненты указываются именами вида [m][d].

Под работой понимается исполнение компонентой {F,D} своей функции F. Работы выполняются в последовательности, указанной стрелками графа работ.

Декомпозиция модели в граф работ поддерживается механизмом обмена данными между модельными компонентами с помощью слотов. Слотом здесь называется специальная переменная компоненты, имеющая следующие свойства. Как переменная слот имеет тип и значение. Слот может представлять массив чисел, строку символов и т.д. Перед началом вычислений слоты инициализируются начальными значениями. Эти значения либо встроены в код компоненты, либо задаются пользователем. Рабочая функция F компоненты M={F,D} может использовать значение своего слота M.X как обычное данное и может изменять его значение. Функция F не может непосредственно изменять слоты других компонент.

Суть в том, что слоты различных компонент могут обмениваться значениями, если они связаны. Таким обменом поддерживается равенство значений связанных слотов. Так, если слот M1.X компоненты M1 связан со слотом M2.Y (это обозначается как M1.X = @M2.Y), тогда изменение компонентой M1 слота M1.X немедленно вызывает такое же изменение значения слота M2.Y другой компоненты. Таким образом, выполняя вычислительную работу, компонента может использовать результаты вычислительной работы других компонент, переданные ей через связанные с ними слоты.

Описания допустимых конфигураций графов работ и связей между слотами компонент помещаются в библиотеку вместе с компонентами модели. Используя такие описания, исполняющая подсистема библиотеки устанавливает связи между слотами перед началом вычисления заданного сценария. При этом если связанная слотами с компонентой M1 компонента M2 не будет найдена, значение слота M1.X не будет изменяться окружением компоненты M1.

Для иллюстрации связи слотов могут изображаться на графе работ пунктирными стрелками.

2.    Представление дерева рекурсии

Рассмотрим представление рекурсий графами работ на примере простейшей рекуррентной последовательности Y n = 0.5* ( Y n 1 + A/Y n 1 ) , Y = 1.5, n >  1, сходящейся к AA . Выражение Y n является арифметическим выражением, и для него можно построить очевидное дерево выражения (дерево рекурсии), которое преобразуется в граф работ, показанный на рис. 1.1. Здесь ромб изображает условную операцию if. Граф 1.2 отличается тем, что дерево выражения Y n 1 + A / Y n 1 представлено кольцевым подграфом, а компонента if агрегирована с компонентой рекурсии [Recur][n]. Пунктирные стрелки изображают передачу результатов вычислений связанными слотами компонент. Чтобы избежать дублирующих вычислений, используются ссылочные компоненты, которые только копируют результат связанной компоненты. Их имена на графах не указываются.

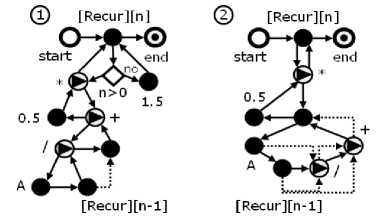
Рис. 1. Граф работ, представляющий рекуррентную последовательность Y _n

Чтобы пояснить работу графа, рассмотрим рекурсивную функцию Func:

double Func(double A, int n)

{ return if n=1 then 1.5 else 0.5*(Func(A,n-1) + A/Func(A,n-1)); } , вычисляющую Yn для действительного числа A и целого n. Напомним, как вычисляется Func. Чтобы вычислить Func(A,n), программа должна сначала вычислить Func(A,n-1). Если она не может этого сделать, например для n>2, она создает в памяти копию Func с параметрами (A,n-1), из которой затем вызывается Func(A,n-2). Если, вызвав Func(A,n-2), программа не может ее вычислить, опять создается ее копия, из которой вызывается Func(A,n-3). И так продолжается до тех пор, пока значение аргумента n в копии Func не окажется равным 1, и программа сможет вычислить Func(A,1). Теперь программа возвращается обратно к предыдущей копии и вычисляет предыдущую копию Func(A,2). Последовательно возвращаясь к предыдущей копии, она вычисляет результат Func(A,n).

Как и функция Func, компонента Recur создает копии подчиненного ей подграфа работ до тех пор, пока не сможет его вычислить. После этого вычисляются предыдущие копии подграфа в последовательности, обратной к последовательности их создания копированием.

3.    Метод прогонки

Решение системы уравнений c 0 u 0 - b0 u1

• -    aiui-1 + ciui - biui+1 = f,    i = 1,2,...,N — 1;(1)

• -    a N u N — i + c N u N =

при условиях

Ic# Ы+|bi|, i =1,2,...,N- 1; |co| ^ |bo| , |Cn| ^ |aN| находится методом правой прогонки как рекуррентная последовательность ui :

ui= ai+1 u+1 + Pi+V; i = N-1,N-2,...0; uN = fN + aNPN ,(3)

cN aNaN где

ai+1 =

bi ci - aiai

P i + 1 = ^{fi + a}i ^e i ; i = 1,2,..., N - 1; c i - a i a i

^a i = ^c о¹ b о , P i = ^c о¹ f >.

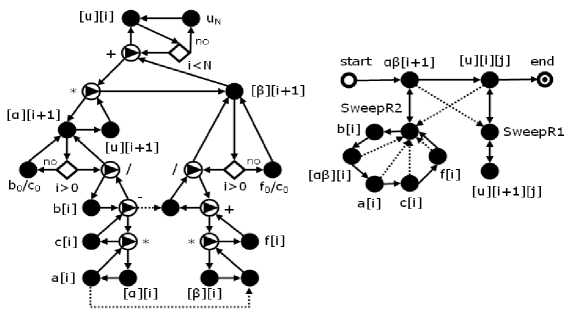
Рис. 2. Граф работ метода правой прогонки

Эти вычисления выполняет граф на рис. 2.1 или его агрегированный аналог на рис. 2.2. Нетрудно построить графы работ для левой и других прогонок.

Компоненты a [ i ], b [ i ], c [ i ], f [ i ] вычисляют одноименные в (1)-(4) параметры a i , b i , c i , f , i = 0,1,..., N . Разнообразие задач, решаемых методами конечных разностей и прогонки, например, задач теплопроводности, диффузии, порождает большое разнообразие зависимостей этих параметров от i. Поскольку концепция сетевой библиотеки не предусматривает для сетевого пользователя неконтролируемую возможность самому программировать формулы, разнообразие таких зависимостей в системе определяется набором дополнительных компонент, с помощью которых можно изменить собственную функциональность компонентов-параметров a [ i ], b [ i ], c [ i ], f [ i ]. Для этого сетевой пользователь подчиняет дополнительные компоненты компонентам-параметрам, включая их в граф, например, так, как показано на рис. 3. Теперь работа, например компоненты b [ i ] , заключается в исполнении работ подчиненными дополнительными компонентами a w [ i ], A_{a 2} [ i ], a a [ i ], A w ₂ [ i ] и в получении значения коэффициента b _v , i уравнения (12).

Компонента аД [ i + 1] помещает в массивы a [] и Д [] значения a [ i + 1] и Д [ i + 1], рассчитываемые компонентой SweepR2 согласно (4). Если компоненты a [ i ], b [ i ], c [ i ], f [ i ] уточняются подчиненными компонентами, как, например, на рис. 3, их значения вычисляются согласно методу уточнения; в противном случае a [ i ] ^ f [ i ] равны постоянным, заданным пользователем при инициализации компонент.

Если неизвестно значение ар\I ], необходимое для вычисления а(3\i + 1], компонента а(3\i ] замещается копией подграфа, подчиненного а(3\i + 1], с параметром i вместо i+1 до тех пор, пока i не окажется равным 1. Тогда ав \1] вычисляет а \1] = c 0¹ b ₀ , Д \1] = c ₀1 f ₀ , и начинается вычисление предыдущих копий подграфа, т.е. прогонка по формулам (4).

После вычисления а \i ] и в \ i ] для i = 1,..., N обратной прогонкой аналогично вычисляется последовательность u \ i ]. Компонента SweepR1 вычисляет значение u i = a _{i + 1} u i _{+ 1} + P _{i + 1} и передает компоненте u \ i + 1], которая помещает его в массив u \] .

4.    Двухфазная модель течения воды и воздуха в пористой среде

Рассмотрим пористую среду (почву), в порах которой протекают две «жидкости»: вода плотности pw и воздух плотности pa. Пусть вода занимает долю 9w единичного объема среды, а воздух - долю 9а. Обозначим через 9p долю пор в объеме среды. Тогда 9w + 9a = 9p, плотность водной фазы равна 9wpw, а плотность воздушной фазы - 9apa. Пусть в водной фазе растворены ионы вида p={Na+, Ca2+,...} с концентрациями Cp , кг-р/кг-Н2О. Малый объем 5Va (t) а -фазы движется так, что сохра няется его масса, т.е. на траектории движения выполняются равенства di\9wPwdVw = -JewdVw , d\9apadVa = 0 ,                           (5)

• d J ⁹ w P w C p^dVw = ^- J ^jp^{d O +} J F p^dVw .

Здесь j p - диффузионный поток ионов вида р из объема 5Vw(t) через элемент его поверхности do, Fp - функция источника ионов. Положив pа = Ра/Pw0 , где Pwо - плотность pw воды в нормальных условиях, получим дифф.-алгебраическую систему dt(9apа)+ div(paJa )= fa , Ja = -ka^Wa - padzr) ;

9wiCp + JwVCp + div(DpVCp)= pw1 Fp ;(7)

9a + 9w = 9p , Va - Vw = Vc (9w ) ;

^p a = P a ( V a ) , k a = k a ⁽⁹ w ) , ^{a e { w} , ^{a }} ;

V w <  0 , V c >  0 , SV c p3(w_w<  0 .

Дифференцируя d ( 9 _a p _a)/ d tt по независимым переменным 9 _w и V _w и усредняя по [ z i _{- 1/2}, z i _{+ 1/2} ] , получим

A ⁽⁹ w , V w ) d_t

9 w

V w

~

⁺ h i

J w ,1 + 1/2    J w ,1' - 1/2

J a,i + 1/2 ^- J a ,i - V2

fw f •

L fa J i

где

J ai - 12

k ai - 12

—.

к va,i  va,i—1

hi

	p w
A (9 w > V w ) =	9 Sp a bV c — . _ a Sva "w °

⁹ w

⁹ a

\

V a ^— P a,i—1(2 ,

J

^P ' ’

Nw SP a

Na J i или                                                                   (11)

^Aw 1, i ⁹ w , i + A w 2, i ^V w , i + ^(— « w , i V w , i — 1 + c w , i V w , i ^— b w , i V w , i + 1 ^{) +} d w , i = ^fw , i ;

Aa 1,i9w,i + Aa2,iVw,i + (— aa,iVw,i—1 + ca,iVw,i — ba,iVw,i+1) + da,i = fa,i , где Aaji - j-я компонента строки a матрицы A(9w vw) из (3) в точке zi. Здесь a = w соответствует первой, a = a - второй строке A(9w,vw). Ус ловиями сопряжения на границе слоев полагаем непрерывность потенциалов Va и потоков Ja .

Положив в(9) vw,i» T Vw,i — vw,i), 9w,i» T (9w,i — ew,i), получимсис- тему (12)-(13), которую будем решать методом правой прогонки:

— «... .vj+ (. + А, Т1 )vj+1 — . Vj++1 = F i,(12)

V,w,—1        V,i         i| w,V,i' w,+1

F v A T ^{— 1} v ww ^+ f v , — d_w, , 9 w + = 9 wi + T A -T¹ F₆., ,

F~/=(.V +\ — .V+1 + b8vw+1i)+ f,-—d6i,(13)

9,1     \  9,1‘  w,i —1       9,1 ‘ w,i        9,1 ‘  w,i + 1 /    9            9,1  'V / где

~ v , i = ^aw , i A a2i — ^aa , i A 2i , ^b V ii = ^b w , - a , li i — ^b a , . A w 2, i , ~ v , i = ~ V , i ⁺ b v , i ;

..

dV,i = dw,iAa2,i da,iAw2,i , fv,i = fw^,iA«2,i fa,iAw2,i ;

~ 9 , i = « a , i A w1,i ^— « w , i A a 1, i , ^b 9 , i = ^ba , i A w 1, i ^{— b}w , i^Aa 1, i , ~ 9 , i = ~ 9 , i ^{+ b} 9 , i ;

N= da,.Aw 1,.-dw,iAa 1,i , k.= fa,.Aw 1,i — fw,,.Aa 1,.^(15)

^a a , i = h ^{— h —} k a ,i — 12 , b a , i = h i — ¹ h i + 1 k a ,i + 1/2 , c a , i = ^a a , i ⁺ b a , i ;

dai = ~—1(ka,i+12/5a,i+1(2 — kai—1/2pa,i—1/2 ) , fa,i = fa(zi) • а Aw1, i , Aw 2, i , Aa 1, i, Aa 2, i - элементы матрицы A (9w ,Vw ) в точке zi , tj •

Систему (12)-(13) решает граф работ на рис. 3, полученный методом уточнения графа на рис. 2. Имена компонент графа отвечают обозначениям (12)-(13) и приводятся здесь без скобок. Имена ссылочных компонент опущены. Очевидно, можно упрощать граф, агрегируя его компоненты.

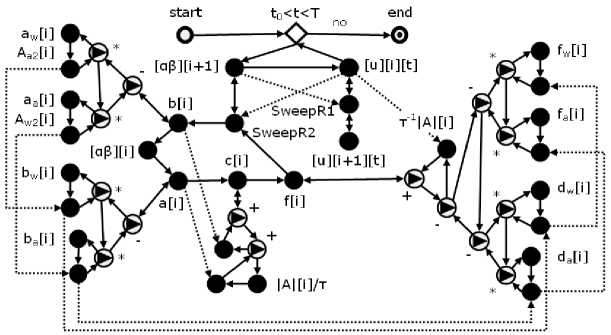
Рис. 3. Граф работ для решения двухфазной модели

5.    Уравнение Ричардса

Рассмотрим частный случай (9), когда др _w (dV^ = 0, V a = Const • Тогда p _w = 1, а 6 _w становится зависимой от w w в силу V a - V w = V c ( P w ) •

Дифференцируя последнее по vw, из (9) получим уравнение Ричардса в полудискретной форме (9)

r ( V w ) -d^ V w , i + иД J w , i + 12 - J w , i - 12 ) = f w , i , r ( V w ) =- $; •

Полагая Vwi ~ т 1 Vi +' 1 — Vwwi) , применим разностную схему i -1    i+1       i ~-1    i+1    _ Tj+1           i r Vw,iT Vw,i   VW,i)+ hi (Jw,i+12 Jw,i—12 ) fw,i ,

из которой с помощью (10) получим систему, решаемую методом правой прогонки i+1               i --1    i+1           i+1 _ ЕЧ

aw,iVw,i-1 + (cw,i + ri T Fw,i bw,iVw,i+1 Fw,i , где aw,i = h?Xhi1 kw,i-12 , bw,i = h?Xhi"+\kw,i+12 , cw,i = aw,i + bw,i ;

^Fw, i = ri ^{T - 1} V wv , i ⁺ f ww , i ^- d w , i , f ww , i = ^fw ⁽ zi , t j ) ,

~

• dw,i   hi

^{( k} w,i + 12 ^p ? w,i + 12 ^k w,i - 12 l ? w,i-1/2 ) •

Система (19) решается следующим графом работ, полученным из графа на рис. 2 методом уточнения аналогично графу на рис. 3.

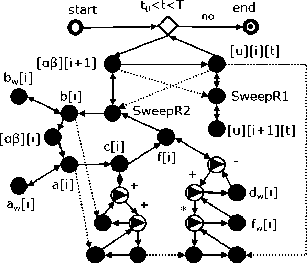
r[i]/T

Рис. 4. Граф работ для решения уравнения Ричардса

Благодарю проф. В.А. Серебрякова, чл.-кор. РАН И.Г. Поспелова и Ю.Н. Павловского, проф. А.М. Тарко, канд. физ.-мат. наук А.А. Бездушного (ВЦ РАН), д-ра физ.-мат. наук Л.Н. Столярова (МФТИ) за обсуждение, критические замечания и внимание к работе.