Интеграционный подход в совершенствовании математического образования

Инновационное развитие современной системы математического образования, появление учебных заведений нового типа (лицеев, гимназий, колледжей и т. п.) требуют коренных изменений и самого процесса преподавания ма-

тематики. Исследования по интеграции математического образования ведутся на математическом факультете и в рамках научно-методической секции математического образования Регионального учебного округа при Мордовском университете. Основным направлением их сотрудничества является интеграция учебных заведений Республики Мордовия с целью совершенствования системы математического образования.

Совершенствование названной системы предполагает: объединение интеллектуального потенциала всех уровней математического образования в системе округа; разработку и апробирование учебных планов и программ по математике для учебных заведений различных типов; решение задач преемственности и непрерывности образования; целенаправленную подготовку одаренных школьников к учебе в вузах, реализацию их индивидуальных творческих запросов и способностей; оказание научно-методической помощи учителям школ и средних специальных учебных заведений в разработке новых форм и методов внеклассной работы по математике; организацию и проведение внутришкольных, районных и республиканских математических олимпиад; изучение, обобщение и про; паганду передовых педагогических технологий; координацию межпредметных связей; разработку тематики и содержания спецкурсов по совершенствованию математической подготовки студентов и учащихся школ; апробирование и издание научно-методических материалов, пособий и учебников для учащихся и преподавателей учебных заведений округа; организацию и проведение научно-методических конференций по вопросам совершенствования преподавания математики в различных учебных заведениях.

Секция проводит в жизнь идеи интеграции разнопрофильных региональных систем образования и использует интеллектуальный потенциал различных учебных заведений — школ, лицеев, гимназий, вузов города и республики. В настоящее время более 20 преподавателей математического факультета МГУ работают в системе „школа — вуз“ Успешно изучаются вопросы дифференциации преподавания математики с учетом направления подготовки учащихся (классы с углубленным изучением математики^

гуманитарные и т. дJ, методики обучения решению задач, логическим приемам доказательства.

Активная работа ведется по линии „университет — школа — МРИПКРО“ Это совместные выездные курсы, математические олимпиады, подготовка к изданию материалов в помощь учителю, планирование и проведение научно-методических конференций.

Большое количество выпускников факультета пишут дипломные работы непосредственно по заявкам учителей математики и МРИПКРО, причем лучшие из них используются в практике преподавания. В журнале „Математика в шко-ле“ опубликованы работы по нестандартным методам решения уравнений и неравенств и нетрадиционным методам преподавания математики, по новым технологиям контроля за обучением математике на факультативных занятиях и уроках в классах с углубленным изучением математики.

Если традиционная система обучения была ориентирована на формирование знаний, умений и навыков, на организацию воспроизводящей деятельности ученика, то сейчас, когда продолжительность жизни знаний во многих областях резко сократилась, в традиционном понимании они уже не могут выступать в качестве основной цели обучения. Специалист должен быть прежде всего носителем творческого начала, способным к нестандартному мышлению. Осуществляемая в настоящее время перестройка среднего образования означает глубокие изменения и в целях, и в содержании, и в формах, и в методах обучения. Совместными усилиями ученых университета, учителей, студентов и аспирантов создаются инновационные методики обучения математике. Эта форма работы приносит удовлетворение ее участникам, так как учителя получают в руки конкретные методические разработки, которые по содержанию дополняют школьные учебники и могут вызвать интерес у учащихся. Работа исследователей в данных проектах строится на сугубо добровольной основе.

Назовем некоторые из исследуемых проблем:

• —    системный подход к составлению задач школьного курса математики;

• —    деятельностный подход к органи-

• зации внеклассной работы пр математике;

• —    нестандартные формы и средства контроля при изучении математики и т. д.;

• —    организация индивидуальной работы на факультативных занятиях по математике;

— процессуальные задачи как эффективное средство развития математического мышления.

Остановимся подробнее на одном из направлений исследований, посвященном нестандартным методам контроля в преподавании математики.

Среди известных методов педагогической диагностики: наблюдения, опроса, анкетирования, тестирования и др., наиболее интересным и нестандартным в процессе обучения математике является метод тестирования. Тест позволяет оперативно организовать самоконтроль, создавая тем самым условия для осознания школьниками результатов учения, помогает им сосредоточить внимание на обобщенных способах действий. Именно в процессе такой деятельности имеется возможность реализовать развивающую функцию обучения. И наконец, тест поддается компьютеризации. Трудная, монотонная, занимающая много времени работа преподавателя может быть успешно выполнена компьютером.

Нами разработаны тестовые задания различных типов (на заполнение пропусков; на определение истинности (ложности) утверждения; с выбором ответа и т. д.) для факультативных занятий в классах с углубленным изучением математики. Важное значение мы придаем задачам, направленным на развитие функционально-графического мышления. Разработанные материалы апробированы в разных типах школ. Практика показала, что более интенсивная работа при тестировании и ее игровой характер повышают заинтересованность учащихся в хорошем результате. Оказывает влияние на нее и ярко выраженная объективность контроля. Даже при неважном результате тестирования у школьников не возникает обиды ни на кого, кроме самого себя.

Приведем один из вариантов тестового задания по теме „Комплексные числа"

ТЕСТОВОЕ ЗАДАНИЕ

Для заданных неравенств (1 — 6):

• а)    найдите (из предложенных шести: А, В, С, D, Е, F) эквивалентные системы или неравенства;

• б)    выберите на рисунках (1 — 18) их геометрические интерпретации.

4. 2 < lz + 1 - 2il < 3,       5. Iz-2I² + lz + 2I² > 26, 3. 1g lz + Sil < 1, 6. 1g lz + Si I il.

Задание 1. Выполните указанные действия.

1. 2 < lz- (1 — 2i) I < 3,     2. lz — 212 + lz + 212 < 26,

lz + Sil < 10,

A1 |z #-Si,

D. Iz + 5il > 10,

B. 4 < (x+1)2+(y-2)2 < 9,    C. x2 + y2>9,

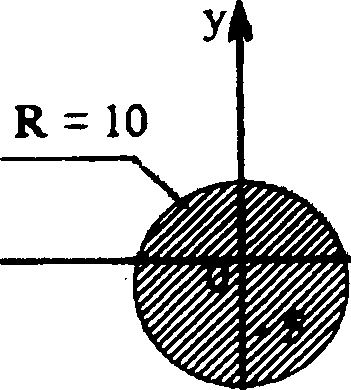
Рис. 1

E. 4 < (x-1)2 +(y+ 2)2 < 9,    F. x2 + y2<9.

R=3 у A                   у A

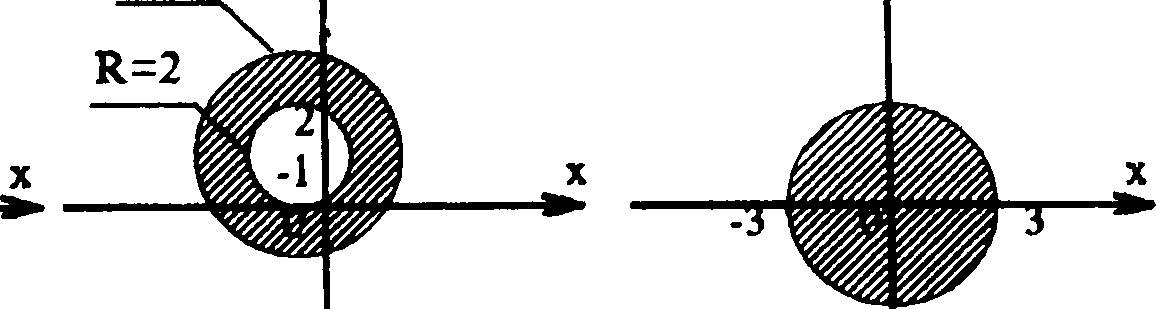
Рис. 3

P и c. 2

Задание 2. Выполните указанные действия.

1. Iz-2I < lz + 10/(i + 2)1, 2. zz < (2 + i)2 + 17/(1 + 4i), 3. lizl < Iz + 8/(1 + i)I, 4. zz > (2 + i)2 + 17/(1 + 4i), 5. Iizl > Iz + 8/(1 + i) 1,     6. Iz- 21 > Iz + 10/(i + 2)1.

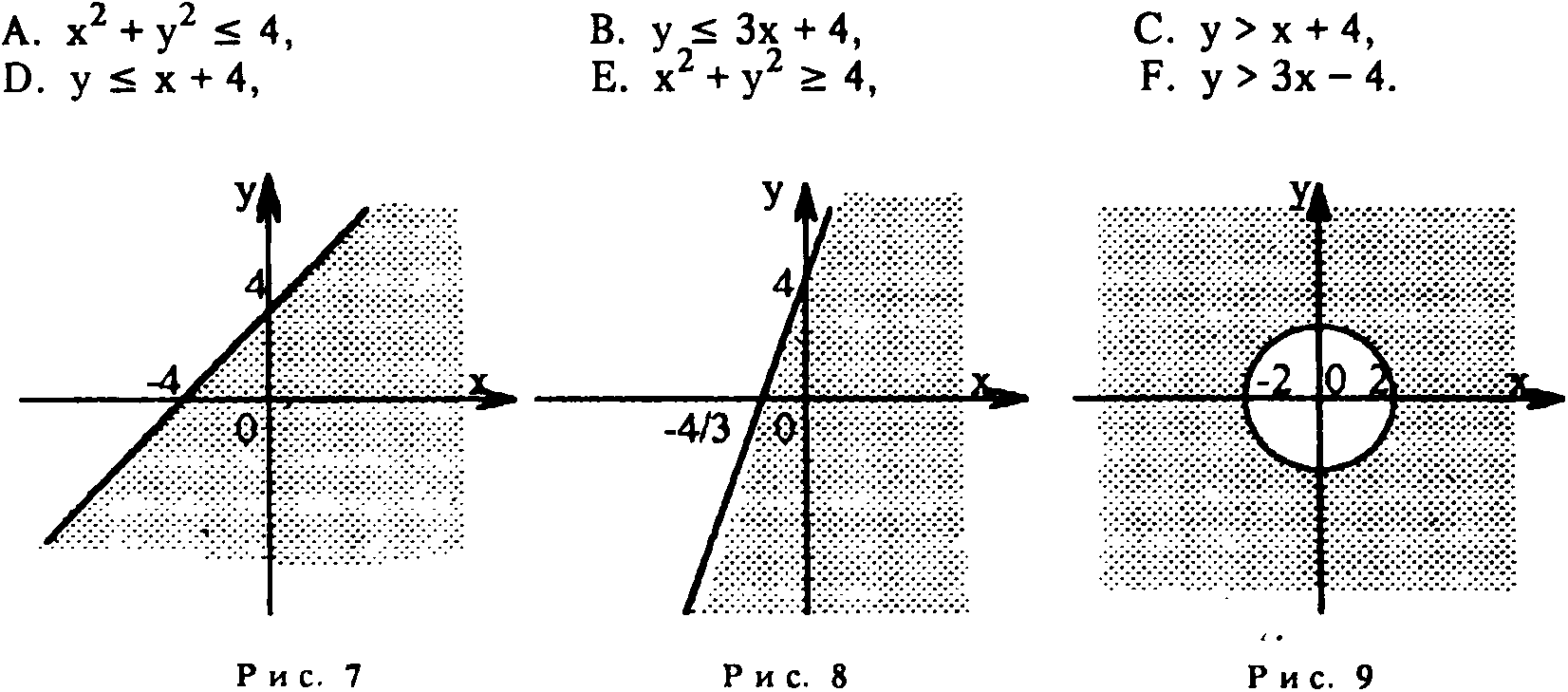
P ис. 10                     P ис. И                       P ис. 12

Задание 3. Выполните указанные действия.

1. Iz + ll/lz-21 > 0,5,

• 4. Iz + 3l/lz-3l <2,

  A.

  
  

• 2.    Iz + 2l/lz-3l > 1, 5. Iz+ 11 /1 z - 21 <0,5,

  B.

  
  

• 3.    Iz + 31 / Iz - 31 5 2,

• 6.    Iz + 2l/lz-3l < 1.

(x - 5)2 + y2 < 16, x + iy * 3,

D. x < 1/2,

(x + 2)2 + y2 > 4, x + iy * 2,

E. (x - 5)2 + y2 > 16,

. Jx>l/2,

- |x + iy * 3,

F. (x + 2)2 + y2<4.

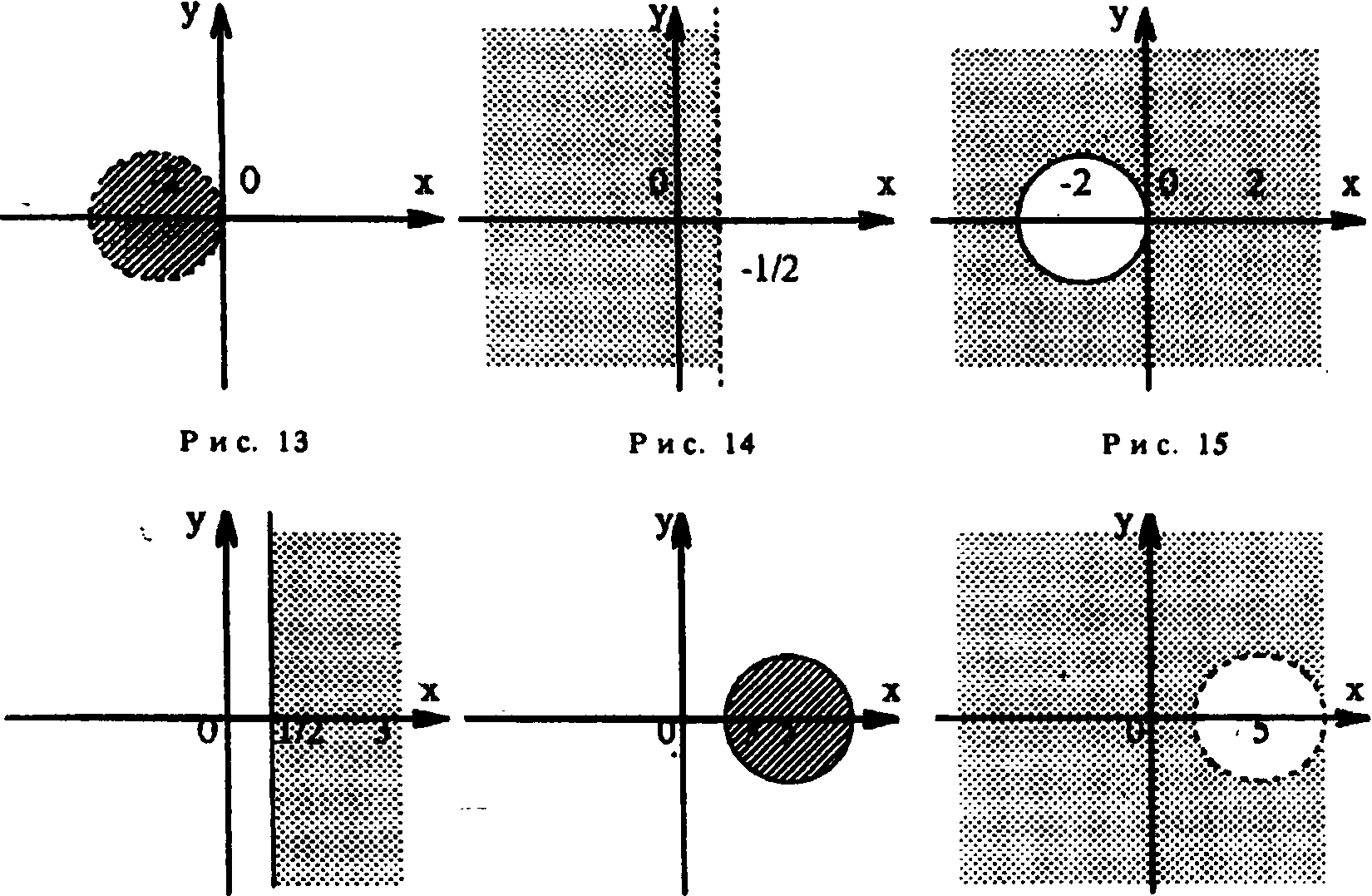
Рис. 16                  Рис. 17                   Рис. 18

ОТВЕТЫ

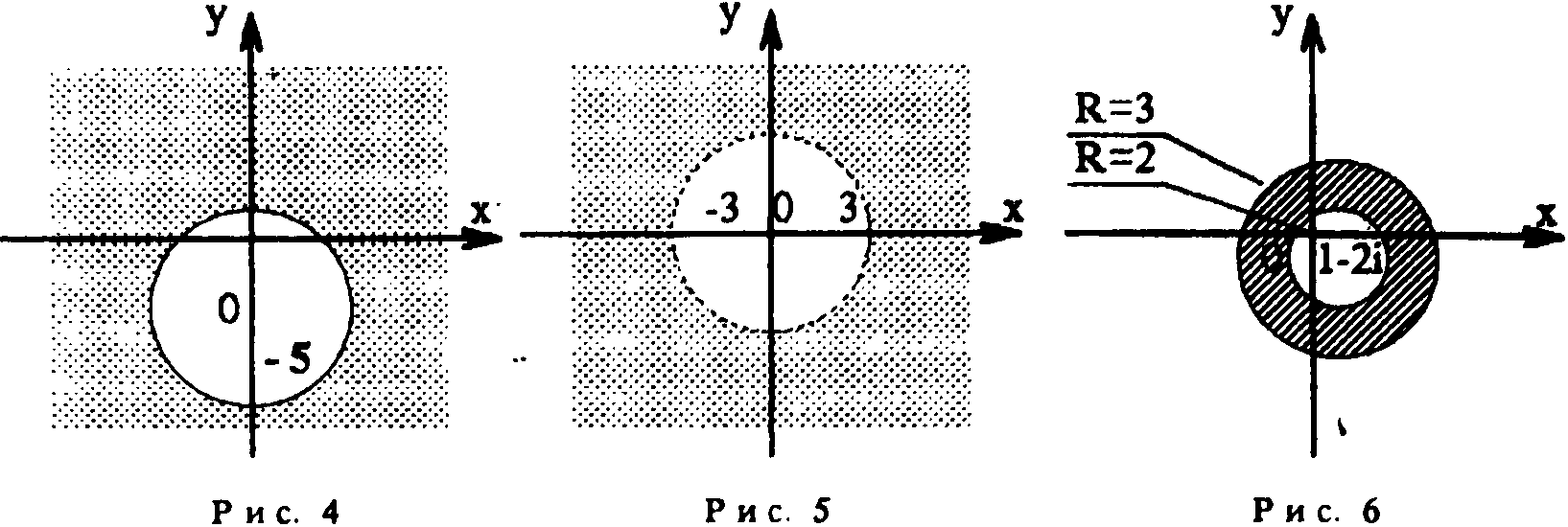
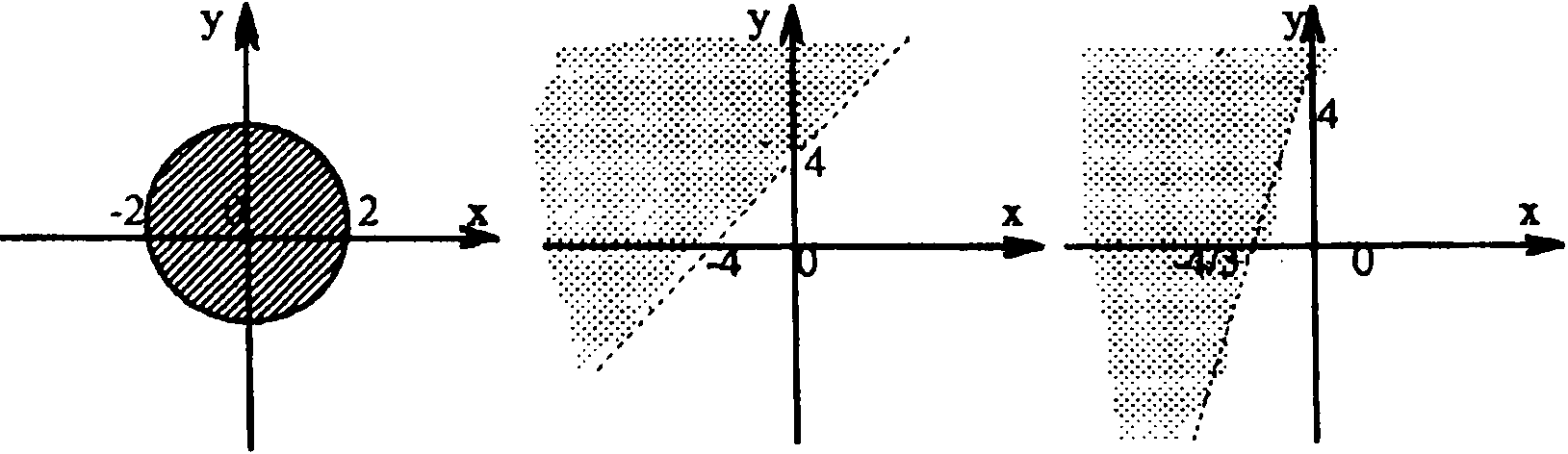
Задание 1. 1 — Е, рис. 6; 2 — F, рис. 3; 3 — А, рис. 1; 4 — В, рис. 2; 5 — С, рис. 5; 6 — D, рис. 4.

Задание 2. 1 — В, рис. 8; 2 — А, рис. 10; 3 — D, рис. 7; 4 — Е, рис. 9; 5 — С, рис. 11; 6 — F, рис. 12.

Задание 3.1 — В, рис. 15; 2 — С, рис. 16; 3 — А, рис. 17; 4 — Е, рис. 18; 5 — F, рис. 13; 6 — D, рис. 14.

В качестве теоретической основы работы нами использованы теория обучения на основе деятельностного подхода, теория индивидуализации обучения и теория развития личности учащихся.

Исследования показывают, что интеграция всех звеньев образовательной системы республики, всех ее направлений и типов учебных заведений дает возмож ность повысить качество подготовки специалистов; обеспечить преемственность в содержании учебных программ и методике обучения в средней и высшей школе; экономить бюджетные средства, оптимально использовать материальные базы вузов и школ; упорядочить содержание и качество управления образованием.