Investigation of the special mechanisms of the high classes

vector equation of independent closed countours MHC fixed coordinate system has the form:

Classification of mechanisms on the second and high classes proposed by I.I. Artobolevsky [1], U.A. Dzholdasbekov [2] requires clarification for the complete solution of the problems of kinematics, kinetostatics and dynamics. Usualy by the mechanisms of general purpose soght arbitrary mechanisms with the Assur group of high classes and by mechanisms of special purpose it is sought the transmission, directive and the transfer mechanism of the high classes (MHC). Such classification allows to develop a general theory of the mechanisms of the first group to identify their functiolities and for the second one to develop the theoretical basis of calculation of the kinematic, force and dynamic parameters and to design of mechanisms with the given characteristics.

ZC +УЬ+ 1 о = 0 ij

where i, j are indexes, whose values range over the number respectively initial and input units, belonging to the considered k - th countour, where — ₀ is the vector of the fixed link.

The equation (1) can be rewritten as

Statement of the problem. Let MHC consists of n mobile units. The numbers of output units vary from 1 to n - m, and of the input with respect to the from the j = n - m + 1 to n. Then nn —

X l = 0 or X l — = 0

i = 0                    i = 0

where li is the absolute value and ^— i is unit

vector of the i-th vector in the corresponding independent countour.

V i = Ф^ф Ф 6 , ^P ) ,   i = 1,^4,

Then the vector equations of the form (1) for a mechanism with a group of Assyrian group of the IV class of the second order with rotational where pairs and two degrees of freedom are represented as (Fig. 1)

P    {l1, l1 ,l2,l3,l3,l4,l5,l6, ai, аз ,l0, ф0 }

l1 + Z2 +I3 +T;-l6 -T, = 0

11* + T* + T4 +T;-i6-i0 = 0

—                                         —

where I, i = 1,2,3,4 I, j = 5,6. The ij asterisk "*" means the membership of the vector

• ^— *

to l_i to the i-th basis link.

The equations (1) and (2) can be represented in projections on the axis of the steady coordinate systems by multiplying them by the — corresponding unit vectors i0 and j0 .

The problem. Find the positions of the output links for the transmission mechanism with a group of Assyrian group of the IV class of the second order with the given desired laws of motion of the input units and dimensional parameters of the MHC:

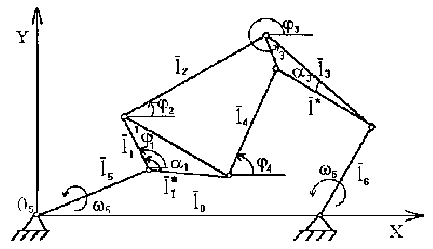
Figure 1 - Mechanism with a Assyrian group of the IV class of the second order and rotational kinematic pairs.

We will follow to the analytic method of the kinematic analysis of arbitrary MHC developed by Mr. B Sinchev in [3].

Solution to the problem. Vector equation (2) MHC represented for k = 2 in the scalar form (in projections) as a system of trigonometric equations

1 1 cos Ф 1 + 1 ₂ cos Ф 2 + 1 ₃ cos Ф ₃ + 1 ₅ cos ф ₅ - 1 ₆ cos Ф 6 - 1 ₀ cos Ф 0 = 0

1 1 sin ф 1 + 1 ₂ sin ф₂ + 1 ₃ sin ф ₃ + 1 ₅ sin ф ₅ - 1 ₆ sin ф ₆ - 1 ₀ sin ф ₀ = 0

l * cos ( ф ₁ - a 1 ) + 1 * cos ( ф ₃ - a ₃ ) + 1 ₄ cos ф ₄ + 1 5 cos ф ₅ - 1 ₆ cos ф ₆ - 1 ₀ cosф ₀ = 0

l * sin ( ф 1 - a 1 ) + 1 * sin ( ф ₃ - a ₃ ) + 1 ₄ sin ф ₄ + 1 ₅ sin ф ₅ - 1 ₆ sin ф ₆ - 1 ₀ sin ф ₀ = 0

with unknown ф 1, .., ф 4 (Fig. 1).

The vector method of eliminating varia-bles reduces the number of unknown varia-bles. Following the vector approach from the first equation of vector equations (3) we find l ₂ and from the second l ₄ that is,

I 2 ^{—-( 1} 1 + 4 M? ^- l 6 ^- l о )

• ¹ 4 ^{—-( 1} 1 + I 3 ^{)-( 1} 5 — ¹ 6 — ¹ 0 }

Next, using the scalar product, we have

^{( 1} 2 ) ^{— ( 1} 1 ^{+ 1} 3 ) ⁺ 2 ^{( 1} 1 ^{+ 1} 3 ^{)( 1} 5 - ¹ 6 - ¹ 0 ^{)+ ( 1} 5 - ¹ 6 - ¹ 0 )

* I²         I * :fe Г            1 *          4; 1 / *          *          * I I *           *          * I²

¹ 4 / ^{- ( 1} 1 ^{+ 1} 3 / ^{+ 2 ( 1} 1 ^{+ 1} 3 ^{)( 1} 5 - ¹ 6 - ¹ 0 ^{)+ ( 1} 5 - ¹ 6 - ¹ 0 /

After simple transformations of the system

——

^— *

(6) to find the vectors l ₁ and l ₁ ^* we

obtain a special system of scalar equations of the

following form:

² ^ 1 ⁺ ^ 5 - , - ^ ) ^

- 1

-

-

¹ 32 -^{( 1}.

^—

-

l 6

-

—      — /—

1 0 ) - 2 1 3 ( 1 5

-

1 6 - — 0 )

— *   —   —   — У*

^\3 + ^5   *6   ^0/1

*

-

-

*2 l ₃

-

^—

-

l 6

-

^— 2 ^— ^— 1 0 ) - 2 1 3 ( 1 5

-

1 6 - — 0 )

It should be noted that l ₁ ^* is associated with l ₁ and l ₃ ^* with l ₃ , where li is module of the — vector l _i the scalar product of vectors l _i

—— —— are     ¹i • ¹i

and (— +1—. )2. In the system (7) the angular coordinates ^2and ^4of vectors —2 and

^— ₄ are eliminate.

Thus we have obtained a special system of algebraic equations, in which the number of equations matches the number of independent closed vector contours.

2(13x3 + I5x5   16x6   10 )11 x1 + 2(13y3 + 15y5   16y6 ) 11 y1 — 12   11

- ^{( 1} 5 x 5 ^{+ 1} 6 x 6 - ¹ 0 ) - ^{( 1} 5 y 5 - ¹ 6 y 6 ) - ^{2 1} 3 x 3 ^{( 1} 5 ^X 5 - ¹ 6 ^X 6 - ¹ 0 ) -

-2l3y3(l3 y3 - l5 y5)

**

2 ( 1 ₃ x ₃ + 1 ₅ x ₅

* *         * *                          * *      2*2

16X6   10 ) 11 X1 + 2(13 y3 + 15y5   16y6 ) 11 y1 — 14

- ¹ 3* - ^{( 1} 5 ^X 5 - ¹ 6 ^X 6 - ¹ 0 ) - ^{( 1} 5 y 5 - ¹ 6 y 6 ) - ^{2 1} 3 ^{( 1} 5 ^X 5 - ¹ 6 ^X 6 - ¹ 0 ) ^X 3 -

- 213(15 y 5 - 16 y 6 )y 3, where x1 = cos(^1), y1 = sin(^1), x* = x1 cos a1 + y1 sin a1,

*

y 1 = x 1 sin a₁ - y 1 cos a₁ ,

x 3 = cos( ^ ₃), y 3 = sin( ^ ₃) , x * = x 3 cos a 3 + y 3 sin a 3 y 3 ,     y * = x 3 sin a 3 - y 3 cos a 3 .

Definition. A mechanism intended for an approximate replay of the given relationship between the angular or linear displacement of input and output units is called a transmission mechanism .

This mechanism belongs to mechanisms for special purposes. Thus, the transmission mechanism shall have certain property and this property is described by the following equation:

e з = f ( e 5 , e б )

Here f given vector function, e ₃ is the singular vector of output link 3.

We transform (8) to the following convenient form:

A 1 x 1 + B 1 y 1 = D1

A 2 x 1       +      B 2 y 1       = D2

• ^x i ⁺ У з = 1 ,

where A 1 = 2(l3x3 + l5x5 - l6x6 - l0) l1, B1 = 2(l3y3 + l5y5 - l6y6) l1,

^D1 = ¹ 2 — ^l i2 — ¹ 32 — ^{( l} 5 x 5 — ¹ 6 x 6 — ¹ 0 ) — ^{( l} 5 y 5 — ¹ 6 y 6 ) —

• - 2I3x3 (l5x5 - I6x6 - I0 )- 2I3y3 (l5y5 - l6y6

A = 2 ( l * x . + Lx, - L x, - L ) l * cos a - 2 ( l * У^ + L У^ - L У a ) l * sin a ,

2     33   55   66   0 1     1    33   55   66 11

*      ***

^B 2 = ^{2 ( 1} 3 x 3 ^{+ 1} 5 x 5 ^{- 1} 6 x 6 ^{- 1} 0 ) ^l 1 sin ^a i ^{+ 2 ( 1} 3 y 3 ^{+ 1} 5 y 5 ^{- 1} 6 y 6 ) ^l 1 cos ^a i ,

^D 2 = ¹ 42 - ^l 1² - ¹ 32 ^{- ( l} 5 x 5 - ¹ 6 x 6 - ¹ 0 ) ^{- ( l} 5 y 5 ^{- 1} 6 y 6 ) ^{-- 2 1} 3 ^{( l} 5 x 5 ^{- 1} 6 x 6 ^{- 1} 0 ) x 3 ^{- 2 1} 3 ^{( l} 5 y 5 ^{- 1} 6 y 6 ) y 3 •

The system (10) is equivalent to the relation

(A1 D2 - A2D1)2     +     (D1 B2 - D2B1)2     -     (A1 B2 - A2B1)2     =0, which is an algebraic equation of sixth degree with respect to x3 or y3 for the mechanism of the IV class of general purpose. The equation (11) is solved only by numerical methods.

Therefore, in the case the mechanism of special purposes, ie, the transmission mechanism should take into account the relation (9). For simplicity, we assume that 1 6 = 0 . Then, the mechanism with two degrees of freedom is the one with one degree of freedom.

Without loss of generality, we can assume that (9) has the explicit form:

^ 3 = 3 ^ 5

and on lengths of links. Then from (10) we find x = D, B2 - D2 B,     ,       = A, D 2 - A2 D,     .

• ¹    A 1 B ₂ - A ₂ B 1      ’ y ¹    A , B ₂ - A ₂ B 1

Substituting these values (14) into (4) and taking into account (12), we find the trigonometric functions x ₂ , y ₂, x ₄, y ₄ .

In conclusion, it can be noted that the above classification and the method developed by author for the first time allowed to find the function of the positions of links (3) of the transmission mechanisms of high classes mechanisms in the explicit analytical form. This approach can be easily extended to the directive and the transfer mechanisms of high classes.

First, we substitute into the known coefficients A ₁, B ₁, D ₁ , A ₂ , B ₂ , D ₂ the angular coordinate (12), then the function x ₃ and y ₃ will acquire the form: