Использование информационных технологий в учебно-методическом обеспечении преподавания геометрических дисциплин

В современном образовательном процессе трудно представить преподавание многих учебных дисциплин без применения компьютеров. Как известно, одним из принципов профессионально -педагогиче -ской направленности обучения является принцип информатизации, который требует широкого использования новых информационных технологий на разных этапах обучения. Их использование предполагает создание новых методик обучения с целью повышения эффективности учебного процесса.

Осуществление процессов геометризации математических знаний и связи их с физической реальностью способствует усилению наглядно-образной составляющей учебного процесса. Пространственное мышление - специфический вид мыслительной деятельности, который необходим при решении задач, требующих ориентации в пространстве, и основывается на анализе пространственных свойств и отношений реальных объектов или их графических изображений.

Основная оперативная единица пространственного мышления-не слово, а образ, воспроизводящий пространственные свойства и отношения объекта (его геометрическую форму, размер, пропорции, положение на плоскости и в пространстве относительно других объектов или наблюдателя со строго фиксированной или произвольно выбранной точкой отсчета). По своему содержанию этот образ отличается от других, отражающих преимущественно не пространственные, а предметные характеристики объектов (индивидуальный облик, цвет, освещенность и т.п.). Умение выделять в объекте его пространственные характеристики и оперировать ими в виде образов формируется особенно отчетливо в тех видах деятельности, где установление пространственных соотношений на основе графической наглядности играет ведущую роль. Иногда это умение обнаруживается довольно ярко как индивидуальная предрасположенность человека выделять в данном материале пространственные отношения и как бы не замечать остальных свойств.

В исследовании Б.М. Блюменфельда [1: 32] экспериментально показано, что опытные шахматисты, решая задачи, оперируют, в основном, образом позиции, т.е. пространственным положением той или иной шахматной фигуры в системе других, а не образом конкретной фигуры как таковой. С равным успехом они могут решать шахматные задачи, пользуясь не только фигурами, но и их заменителями: фишками, камешками и т.п. Решение задач обеспечивается здесь быстрым нахождением правильной пространственной комбинации фигур путем мысленного их перемещения, что предполагает наличие четкого образа, отражающего в основном динамические пространственные соотношения фигур.

Образовательная практика свидетельствует о том, что недостаточное развитие пространственного мышления препятствует эффективному усвоению геометрии, особенно в старших классах средних общеобразовательных школ при переходе к стереометрии, существенно затрудняет овладение графическими дисциплинами в вузе.

В настоящее время создаются школьные учебные программы по геометрии, которые во всем многообразии образовательных целей решают три основные задачи:

• - преодоление существенного разрыва между изучением плоских и пространственных фигур;

• -    создание у учащихся гибких многомерных пространственных образов, включающих в единстве топологические, проективные, метрические свойства и отношения изучаемых объектов;

• -    сочетание инвариантного и вариативного учебного материала, позволяющего учитывать познавательный профиль ученика, его индивидуальные способности.

Рис. 1

Современная методика обучения геометрии должна опираться на анализ и проектирование тех видов учебной деятельности, которые обеспечивают овладение ее научным содержанием. Среди этих видов деятельности выделим два основных: создание пространственных (геометрических) образов; оперирование исходными образами в процессе решения различных геометрических задач.

В качестве заданий, позволяющих выявить процесс создания образа, можно использовать следующие:

• -    перевод словесных данных задачи в графический образ;

• -    выделение искомой фигуры из других фигур чертежа;

• -    построение недостающих фигур чертежа по ходу решения задачи;

• -    рассмотрение элементов чертежа с разных точек зрения, включение их в разные фигуры.

При изучении математики студенты резко дифференцируются не только по разным показателям уровня развития пространственного мышления, но и по способам решения задач. Это позволяет выявлять «познавательные стили» студентов при обучении математике, которые, как показывает опыт, носят устойчивый характер, проявляются у одного и того же человека при работе над созданием геометрического образа, оперировании им, что способствует становлению различных типов математического интеллекта [2]: алгебраист-геометр; теоретик-практик; склонный к аксиоматическим рассуждениям - опоре на наглядную агитацию.

Подчеркнем важность совершенствования фундаментальной геометрической составляющей как основы повышения качества подготовки специалистов физикоматематического направления в университете. Чрезмерная формализация процесса обучения высшей математике (особенно на гуманитарных специальностях) приводит к потере принципа наглядности, т.е. наглядная образность как инструмент научного познания и дидактический принцип утрачивает свой приоритет. Возникает необходимость дезабстрагирования и конкретизации математических знаний применительно к обучению.

Процесс геометризации математических знаний способствует усилению нагляднообразной составляющей учебного процесса в преподавании дисциплины «Аналитическая геометрия», курсов по выбору и решает задачу разработки методических систем, основанных на максимальном использовании образно-ассоциативного способа переработки математической информации.

С учетом вышесказанного на основе объектно-ориентированного языка Java [3] одним из авторов создан комплекс обучающих программ по аналитической геометрии. Используя пакет динамической геометрии, студенты могут создавать фигуры и различные объекты и исследовать их. Естественно, наглядность и четкость образов делают процесс изучения геометрии более увлекательным и позволяют привить студенту интерес к предмету. Одним из важных достоинств этого комплекса программ является возможность работы с трех-

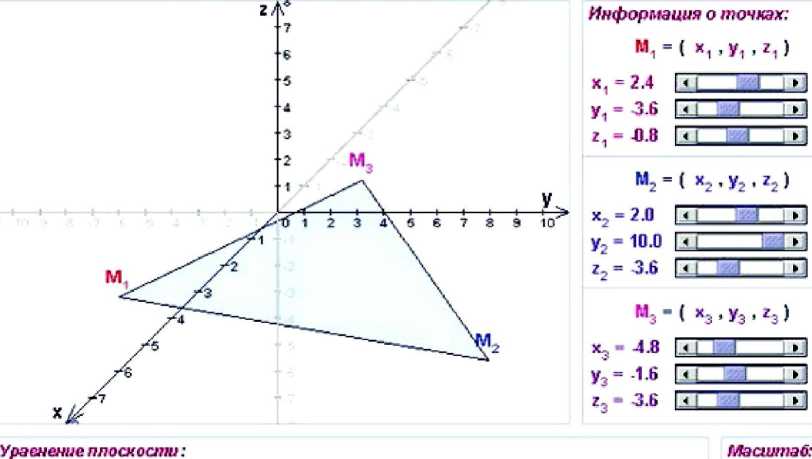
Уравнение плоскости, проходящей через 3 точки

= 0

= 0

-3.6 + 0.8

<3.6 +0.8

х -2.4

2.0 -2.4

У + 3.G

10.0 + 3.6 -1.6+3.6

х-х1 у-у, z-z1

*2-^ Уз-Vt ^г_г-^г, ^хз’*1 Уз-¥₁ z₃-^zi

Рис. 2

мерной графикой, позволяющей обучаемому строить реальные объекты, создавать проволочную модель, окрашивать лицевую и внутреннюю стороны поверхности, отображать объект в различных проекциях (см. рис.1).

Имеется возможность вычисления объемов пространственных тел, площадей плоских фигур при заданности только необходимых параметров. Рассматривается процесс построения различных типов уравнений прямых на плоскости, уравнений плоскости в пространстве (рис. 2).

Динамические возможности обучающего комплекса, реализованного на базе языка Java, можно использовать не только для демонстрации геометрических объектов, способов их построения, но также как графическую среду для выполнения учебного проекта, исследовательской деятельности.

Обобщая вышеизложенное, выделим области применения информационных технологий с педагогическими целями их использования при изучении студентами дисциплины «Аналитическая геометрия»:

• -    обучение построению компьютерных объектов по заданным параметрам;

• -    формирование умения строить трехмерные стереометрические изображения по данным двумерным объектам;

• -    обучение использованию компьютера для создания и преобразования графических образов;

• -    формирование умения выполнять геометрические преобразования в динамическом представлении;

• -    обучение использованию информационных технологий для исследования математических и создания собственных моделей.