Использование явлений реальности в обучении математике образовательный потенциал

Концепция математического образования в школе и вузе нацеливает на формирование представлений об идеях и методах математики, о математике как методе описания и методе познания реальной действительности; на овладение конкретными знаниями, необходимыми для практической деятельности; на воспитание личности и интеллектуальных умений, необходимых для полноценной жизни в обществе.

Реализация указанных направлений в процессе овладения современным содержанием математического образования требует системного подхода и комплексного изучения рассматриваемых явлений.

Проблема использования реальности в обучении математике (РОМ) (вместе с такими аспектами, как связь математических дисциплин с профессиональной направленностью обучения, использование историзма. реализация межпредметных связей математики, политехнизм, прикладная и практическая направленность обучения математике и т.д.) привлекала и привлека ет внимание исследователей и является одной из приоритетных проблем теории и методики обучения математике.

Однако составляющие данной проблемы изучаются изолированно, трактуются достаточно произвольно. Это приводит к большому числу рекомендаций, порой противоречащих друг другу (таковы, например, требования, предъявляемые к понятиям прикладных и практических задач). Отсутствует понятийный аппарат, необходимый для отражения всей совокупности материалов, раскрывающих взаимосвязи математики и реальности в процессе обучения (материалов РВМиРвПО). Практически полностью «выпала» из рассмотрения теории и методики обучения математике совокупность нестандартных задач РВМиРвПО, не являющихся прикладными (свыше 15 типов).

Таким образом, односторонние подходы к проблеме использования реальности в обучении математике не позволяют выделить всю совокупность теоретических положений, составляющих научную основу

концепции РОМ. Такую основу можно создать при комплексном подходе к этой проблеме. рассматривая РОМ как методическую систему. Современные концепции процесса обучения, учебного познания,психологические закономерности усвоения знаний, практика обучения математике обусловливают необходимость системного, комплексного подхода к постановке и решению проблемы использования реальности в обучении математике.

Исходя из того что потенциал (от лат. potentia - сила, возможность) есть источники, возможности, средства, которые могут быть применены для достижения каких-либо целей, решения каких-либо задач в определенной области, под образовательным потенциалом РОМ будем понимать средства, возможности использования явлений реальности в обучении математике, которые могут быть применены для достижения образовательных, воспитательных и практических целей математического образования. решения задач математического образования.

Компоненты образовательного потенциала РОМ следующие.

• 1.    Природа математического знания. Предмет и методы математики, ее ведущие идеи и понятия. (Сущность и происхождение математических абстракций. Соотношение между математическими абстракциями и реальной действительностью. Развитие предмета математики. Место математики в системе наук).

• 2.    Феномен математики как метода познания реальной действительности и орудия преобразующей деятельности человека. (Связь математики с другими науками и практикой. Математика как необходимое условие ускорения НТП и непосредственная производительная сила общества. Роль математического моделирования в научном познании и практике).

• 3.    Гносеологический процесс познания в математике. Методы научного познания (общие и специфические для математики).

• 4.    Формирование научной картины мира и научного мировоззрения.

• 5.    Развитие нравственных черт личности. формирование системы гуманистических взглядов и убеждений.

• 6.    Гуманизация и гуманитаризация общего математического образования.

• 7.    Творческая хнебно-познавательная деятельность. Развитие творческих способностей школьников. Формирование и развитие математического стиля мышления, культуры мышления

• 8.    Эстетика математики. Эстетическое воспитание школьников

• 9.    История математики.

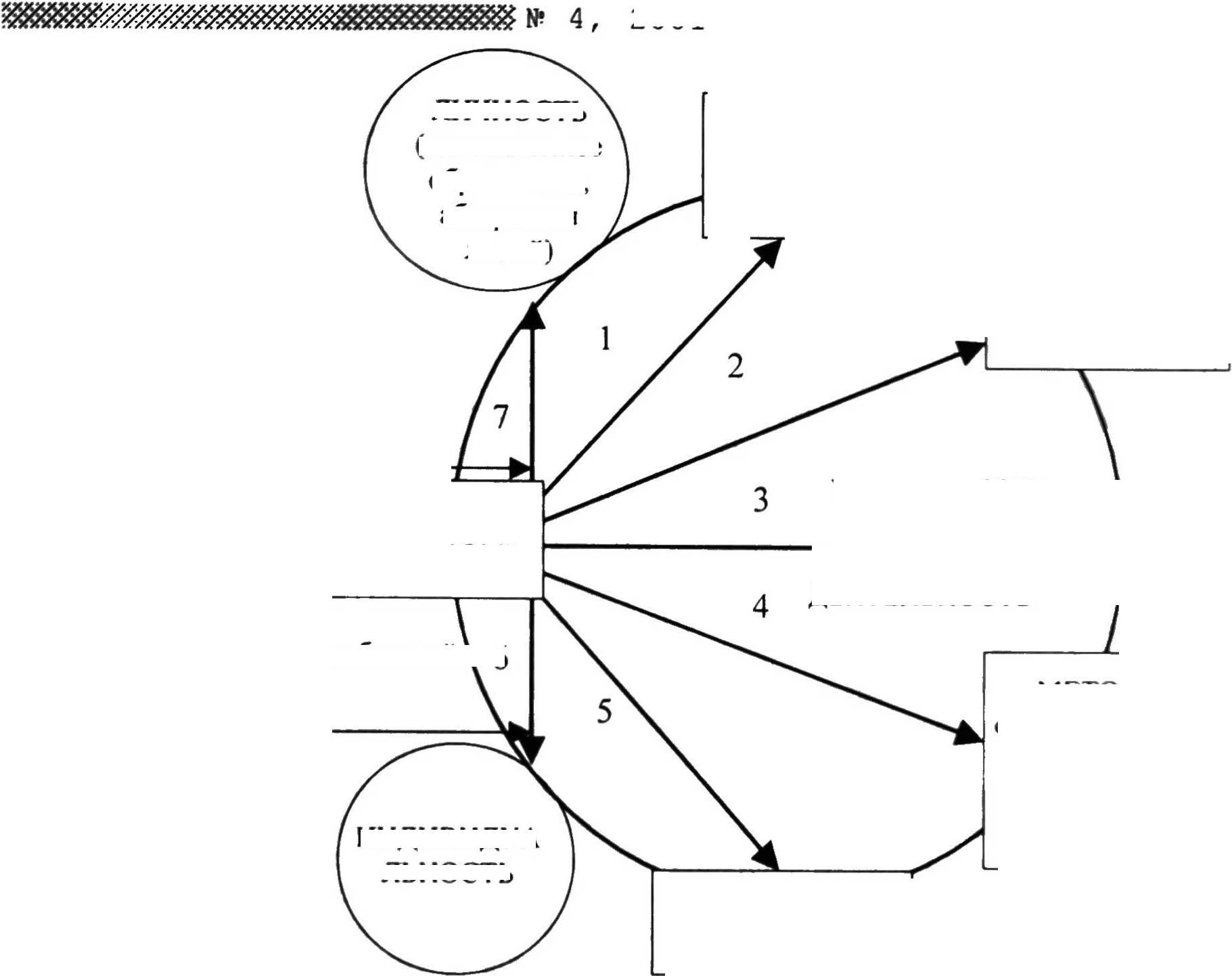
Современными концепциями процесса обучения, учебного познания, психологическими закономерностями усвоения знаний, особенностями математического знания и его усвоения, практикой обучения математике обусловлено то, что реальность в обучении математике предстает как многогранное явление, а именно (рис. I):

• 1)    средство реализации целей обучения;

• 2) средство целенаправленного формирования и развития знаний, навыков, умений;

• 3)    способ организации, управления и стимулирования учебно-познавательной деятельности;

• 4)    способ реализации методов, форм и средств обучения;

• 5)    способ применения знаний, навыков, умений (связи теории с практикой) и средство проверки, оценки и коррекции знаний, навыков, умений;

• 6)    средство реализации индивидуальных черт, способностей, интересов личности;

• 7)    средство формирования и развития мотивационно-потребностного, операционно-содержательного и эмоционально-волевого компонентов личности.

Анализ истории формирования начальных математических представлений позволяет сделать заключение о том, что математические знания возникли из практического опыта и являются математическими моделями объектов реальной действительности. Реальность служит источником возникновения и развития математического познания человека: и самой математики как науки, и математики - учебного предмета

Начиная с античного периода развития математического познания в обучении математике (и в самой математике) постепенно складывалась ситуация, когда прикладные аспекты использования матема-

2001?

ЦЕЛИ обучения

СОДЕРЖАНИЕ обучения

ЛЬНОСТЬ

ЛИЧНОСТЬ

УЧЕБНО-ПОЗНА-

МЕТОДЫ, организационные ФОРМЫ, СРЕДСТВА обхчения

РЕЗУЛЬТАТЫ обучения

Рис. 1. Теооетическая модель «Реальность в обучении математике»

СРЕДСТВО формирования и развития мотивационного, операционно-содержательного, эмоционально-волевого компонентов личности

(как системное

образование,

аостракция

людей)

РЕАЛЬНОСТЬ

В ОБУЧЕНИИ МАТЕМАТИКЕ (РОМ)

СРЕДСТВО реализации индивидуальных черт, способностейД 6 интересов учащихся

ИНДИВИДУА

► ВАТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ

тических знаний в человеческой деятельности периодически уступали доминирующую роль проблемам и задачам «чистой» математики. Отчетливо такая ситуация наблюдалась, например, в обучении математике (и в отношении самой математики) в Древней Греции и в системе традиционного математического образования, сложившейся в конце XIX - начале XX столетия как в России, так и за рубежом.

В дальнейшем линия усиления связи обучения математике с жизнью, политехнической направленности математического образования, прикладной и практической направленности обучения математике, использования явлений РОМ стала одной из наиболее приоритетных в теории и методике обучения математике. При этом можно выделить такую важную особенность, связанную с использованием РОМ. как тенденцию амплификации (расширения) понятий. отражающих совокупность материалов РВМиРвПО: каждое последующее понятие (политехнизм, прикладная и прак тическая направленность, реальность в обучении математике) включает в себя содержание предыдущего понятия и добавляет новые компоненты.

Проанализируем более детально роль и место РОМ в процессе реализации наиболее значимых направлений математического образования (А - Г).

• А.    Реализация гуманитарного потенциала школьного курса математики посредством использования явлений РОМ

С опорой на совокупность существующих ныне исследований осуществлено выделение гуманитарного потенциача математики (ГПМ) в содержании общего математического образования, который включает в себя следующие направления и компоненты: 1) предмет и метод математики, ее ведущие идеи и понятия, связь с другими науками и практикой (математическое моделирование), математический язык; 2) процесс познания в математике; математика как метод познания природы и общества; 3) специфика творче ской матема- 63

тической деятельности; 4) методы научного познания (как общие, эвристические и логические, так и частные, специфические); 5) культура мышления, включающая и стиль научного мышления; формирование научной картины мира, научного гуманистического мировоззрения, нравственное и эстетическое воспитание; 6) история математики как часть общечеловеческой культуры.

Анализ проблемы реализации гуманитарного потенциала математики посредством использования РОМ позволяет заключить, что РОМ есть средство совершенствования школьного учебного процесса, использование которого является необходимым фактором реализации основных компонентов и направлений (80 %) ГПМ.

Б. Формирование математического мышления и развитие творческих способностей школьников посредством использования явлений РОМ.

Анализ работ исследователей в данной области позволяет сделать следующие выводы: 1) мышление является основой всей познавательной деятельности учащихся; развитие мышления происходит от конкретного к абстрактному, и от него к практике (конкретному); 2) математическое мышление (как часть мышления вообще) обладает присущими ему специфическими особенностями: а) в состав математического мышления входят конкретное мышление, абстрактное, интуитивное, функциональное; б) существуют три формы математического мышления: понятия, суждения, умозаключения; в) математическому мышлению присущи такие качества, как глубина, гибкость, критичность и др.

В психолого-педагогической и методической литературе выделяется совокупность умений, присущих творческой деятельности, и ее характерных признаков: 1) умение видеть проблему в знакомых, стандартных для субъекта ситуациях; самостоятельность комбинирования известных способов деятельности в новый, нетрадиционный способ; 2) умение рационально использовать полученную информацию; способность к анализу и обобщению содержания явлений, не связанных очевидной внешней связью; 3) видение структуры объекта, подлежащего изучению; 4) способность выделить новые функции знакомого объекта; 5) способность к рефлексии, к поиску и осуществлению оригинального способа решения при известности других способов; 6) самостоятельность в переносе знаний и умений в новую ситуацию: а) ближнюю; б) дальнюю; 7) способность к моделированию и гибкому решению возникающих проблем и т.д.

Исследование проблемы формирования математического мышления и развития творческих способностей школьников посредством использования РОМ позволяет заключить: 1) использование РОМ является необходимым фактором при формировании всех (100 %) основных компонентов математического мышления школьников (конкретного, абстрактного, интуитивного, функционального); 2) формирование значительной части (около 70 %) компонентов совокупности умений, присущих творческой деятельности учащихся в школьном учебном процессе, эффективно реализуется посредством использования РОМ.

• В.    Разрешение противоречий школьного учебного процесса посредством использования явлений РОМ.

Противоречивость мира, его двойственный характер предопределяют и противоречивый характер школьного учебного процесса, поскольку процесс обучения и воспитания является частью реальной действительности. Осмысление противоречий педагогической сферы - непременное условие работы педагога с детьми. Философский взгляд на воспитание, обнаруживающий его внутренние противоречия, определяет педагогическую стратегию. Учет противоречий определяет также и педагогическую тактику, и соответствующую систему методик, которые используются педагогом в учебном процессе.

С опорой на соответствующие работы в области теории и методики обучения математике, на психолого-педагогические исследования данной проблемы представляется возможным выделить следующий ряд противоречий:

• 1)    между повседневной коллективной работой школьников и индивидуальными особенностями усвоения ими знаний;

• 2)    между объемом и содержанием учебного материала;

• 3)    противоречие целей обучения;

• 4)    противоречие сущности учебного процесса (между преподаванием и учением);

• 5)    противоречие содержания изучаемого;

• 6)    противоречия, возникающие в процессе усвоения знаний;

• 7)    между прямой и обратной связью в обучении;

• 8)    противоречие, выражающееся в несоответствии между уровнем интереса учащихся и важностью изучаемого;

• 9)    между задачами разностороннего общего образования и узкопрофессиональным, ограниченным кругом интересов части учеников и др.

Резюмируя анализ проблемы разрешения противоречий в процессе обучения математике в средней общеобразовательной школе, можно сделать следующий вывод: РОМ является средством совершенствования школьного учебного процесса, использование которого выступает необходимым фактором разрешения значительной части (около 90 %) противоречий в обучении математике учащихся средней школы.

Г. Роль и место РОМ при формировании научного мировоззрения учащихся.

Исследование данной проблемы позволяет заключить: 1) использование РОМ является весьма важным фактором (а в ряде случаев необходимым условием) формирования мировоззрения школьников. Реализация более половины (около 60 %) основных направлений формирования научного мировоззрения учащихся осуществляется посредством использования РОМ; 2) соответственно реализация существующих методик использования РО^ служит необходимым условием формирования и развития научного мировоззрения школьников.

Проанализируем содержательные компоненты феномена РОМ.

Традиционными содержательными компонентами процесса реализации РОМ являются следующие:

• 1)    историзм в обучении математике; 2)межпредметные связи математики;

• 3)    профессионально ориентированная напра&ченность обучения математике;

• 4)    политехнизм, политехническая направленность математического образования;

• 5)    прикладная и практическая направленность обучения математике.

Прикладная направленность обучения математике - это содержательная и методологическая связь школьного курса с практикой, которая предполагает формирование у учащихся умений, необходимых для решения средствами математики прикладных задач.

Развитие у учащихся правильных представлений о природе математики и об отражении ею явлений реального мира — программное требование к обучению математике. Доминирующее средство реализации этой цели - прикладная и практическая направленность математического образования. Основным средством реализации прикладной направленности выступают практические и прикладные задачи. Но это - ^е единственный и исчерпывающий вид задач РВМиРвПО, успешно используемых в школьном учебном процессе. Существует совокупность задач и материалов РВМиРвПО, которые обладают значительной образовательной ценностью, но которые не являются прикладными задачами - в них не используется метод математического моделирования или его использования явно недостаточно для получения ответов (результатов) этих заданных ситуаций. Метод их решения - не «чисто» математический, не только математический или даже вовсе не математический. Такие задачи решаются с помощью аналогии, синтеза, обобщения понятий, установления взаимосвязей и т.д.

Исходя из опыта работы с задачами РВМиРвПО, не являющимися прикладными, представляется возможным выделить следующие их типы:

• 1)    задачи, направленные на выявление взаимосвязей;

• 2)    задачи, в которых необходимо привлечение и применение метода аналогии, требуется осуществить выявление различий, установить противоположности или антиподы;

• 3)    задачи, для решения которых необходимо привлечение, помимо математических, методов исследования других наук;

• 4)    задачи, которые не разрешимы или не решаются средствами школьного курса на данном уровне знаний учащихся, но которые имеют значительный образователь-

• ный и педагогический потенциал (легенда о Делосском жертвенном кубе, задача-экзамен жрецов бога Ра и т.п.);

• 5)    задачи, в которых необходимо осуществить практическую демонстрацию или эксперимент, имеющие нематематический или не только математический характер решения;

• 6)    задачи, в процессе решения которых необходимо установить причинно-следственные отношения между данными объектами, процессами или явлениями, выстраивать причинно-следственные «цепочки»;

• 7)    задачи, процесс разрешения которых осуществляется в форме дидактических игр и является не чисто математическим, не только математическим или нематематическим;

• 8)    задания РВМиРвПО следующего вида: закончите прерванную фразу, рассказ, сюжет; вставьте в пропуски слово, термин, имя и т.п.; поставьте разумные вопросы (задайте возможные вопросы); восстановите ответ (восстановите вопрос); установите, где можно увидеть проявления этих математических закономерностей или фактов в окружающей жизни; выясните, где и в каких областях применяются такие способы; установите, как это используется, например, в технике и т. д.

Содержательная модель РОМ (рис. 2) включает в свой состав как «традиционные» компоненты из тех, что перечислены выше, так и указанные заданные ситуации РВМиРвПО, которые не являются прикладными задачами.

межпредметные связи

политехнизм историзм

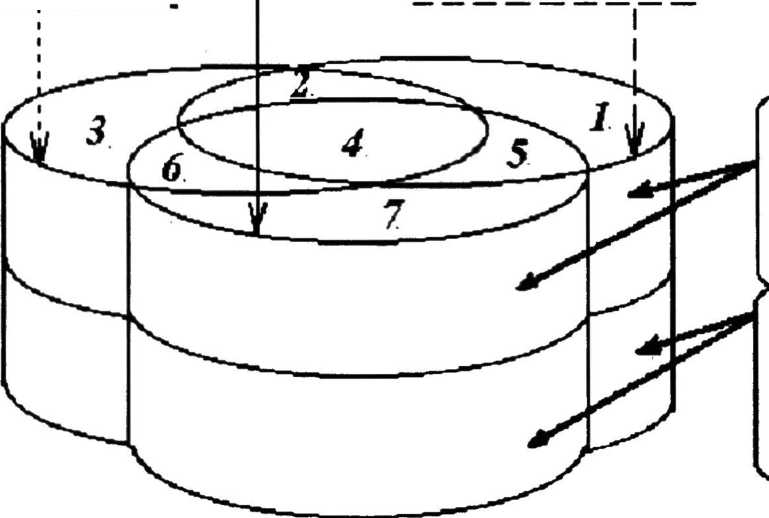
Материалы и задачи РВМиРвПО, не являющиеся прикладными задачами Прикладная и практическая направленность; ПРИКЛАДНЫЕ

ЗАДАЧИ

Рис. 2. Содержательная модель «Реальность в обучении математике»

Резюмируя сказанное выше, заметим следующее.

• 1.    Традиционные односторонние подходы к проблеме использования явлений реальности в обучении математике не позволяют выделить всю совокупность теоретических положений, составляющих научную основу концепции РОМ. Современные концепции процесса обучения, учебного познания, психологические закономерно-

• сти усвоения знаний, практика обучения математике обусловливают необходимость системного, комплексного подхода к постановке и решению проблемы использования реальности в обучении математике.

• 2.    Исследование проблемы реализации образовательного потенциала реальности в обучении математике позволяет установить, что:

Ж№^ 4,

• -    формирование свыше половины (70 %) компонентов совокупности умений, присущих творческой деятельности учащихся в школьном учебном процессе, реализуется посредством использования явлений РОМ;

• -    формирование всех (100 %) основных компонентов математического мышления школьников (конкретного, абстрактного, интуитивного, функционального мышления) реализуется посредством использования реальности в школьном процессе обучения математике;

• -    реализация 60 % направлений процесса формирования и развития научного мировоззрения учащихся в школьном учебном процессе осуществляется на основе использования РОМ;

• -    формирование и развитие свыше 80 % компонентов и направлений реализации гуманитарного потенциала математики в содержании общего математического образования реализуется на основе использования РОМ;

• -    разрешение большинства (около 90 %) противоречий школьного процесса обучения осуществляется посредством исполь

  
3. Системный анализ изучаемого явления позволяет охарактеризовать реальность в обучении математике со всех сторон учебного процесса. РОМ представляет собой системное явление, обладающее следующими основными характеристиками (признаками): I) служит средством реализации целей обучения; 2) средством целенаправленного формирования и развития знаний, навыков, умений; 3) способом организации, управления и стимулирования учебно-познавательной деятельности; 4) способом реализации методов, форм и средств обучения; 5) способом применения знаний, навыков, умений (связи теории с практикой) и средством проверки, оценки и коррекции знаний, навыков, умений; 6) средством формирования и развития мотива-ционно-потребностного, операционно-содержательного и эмоционально-волевого компонентов личности; 7) средством реализации индивидуальных черт, способностей, интересов личности.

зования реальности в обучении математике.