Исследование корреляций между результатами ЕГЭ по математике абитуриентов и их успеваемостью в вузе

Качество образования является значимым фактором для любой страны, однако, как свидетельствует статистика, по этому параметру Россия теряет свои позиции.

Об этом свидетельствуют, например, опубликованные недавно итоги исследования ОЭСР «Международной программы по оценке образовательных достижений учащихся» (PISA) за 2012 г. [3].

PISA — тест, оценивающий грамотность школьников в разных странах мира и умение применять знания на практике. Проходит раз в три года. Был разработан в 1997 г., впервые прошел в 2000 г. В исследовании 2012 г. основное внимание уделялось математической грамотности и выявлению тенденций развития математического образования в мире за последние годы.

В тесте 2012 г. принимали участие около 510 тыс. подростков в возрасте от 15 лет 3 месяцев до 16 лет 2 месяцев из 65 стран. Тест состоял из различных вопросов и заданий по математике, естествознанию и чтению.

Согласно итогам исследования PISA за 2012 г. (таблица 1), лучшее среднее образование — в странах Восточной Азии: Шанхай (Китай), Сингапур, Гонконг (Китай), Тайвань, Республика Корея; в Европе в десятке лидеров — Финляндия, Польша, Швейцария, Нидерланды.

Во всех трех исследованиях и по всем трем направлениям российские школьники показали результаты ниже среднего по ОЭСР уровня.

Кроме отставания в обычной школе, Россия потеряла лидерство по подготовке та-

Таблица 1

Итоги исследования PISA за 2012 г.

Programme for International Student Assessment, PISA (2012)
Maths		Sciences		Reading
1	Shanghai, China	1	Shanghai, China	1	Shanghai, China
2	Singapore	2	Hong Kong, China	2	Hong Kong, China
3	Hong Kong, China	3	Singapore	3	Singapore
4	Taiwan	4	Japan	4	Japan
5	South Korea	5	Finland	5	South Korea
6	Macau, China	6	Estonia	6	Finland
7	Japan	7	South Korea	7	Taiwan
8	Liechtenstein	8	Vietnam	8	Canada
9	Switzerland	9	Poland	9	Ireland
10	Netherlands	10	Liechtenstein	10	Poland
34	Russia	37	Russia	42	Russia

Таблица 2

Суммарные результаты международных олимпиад за последние пять лет

Страна	Золотые Медали	Серебряные медали	Бронзовые медали	Участники без медалей
Китай	28	1	1	0
Ю. Корея	20	9	0	1
США	20	9	0	1
Россия	19	11	0	0
КНДР**	10	10	4	0
Таиланд	9	19	2	0

Окончание табл. 2

Страна Золотые Медали Серебряные медали Бронзовые медали Участники без медалей Япония 9 15 4 2 Канада 9 9 11 1 Иран 8 17 7 0 Турция 8 14 8 0 Тайвань 7 20 1 2 Румыния 7 14 8 1 Вьетнам 7 12 11 0 Великобритания 7 9 11 3 Сингапур 6 14 7 2 Украина 6 11 11 2 Италия 5 12 7 6 ** Без результатов 2010 г., когда команда была дисквалифицирована. лантов мирового уровня. Так, на международных математических олимпиадах последних лет наблюдается снижение результатов. Традиционно высокие первые-вторые ме ста России сменились на непризовые места в последние годы. В таблице 2 приведены суммарные результаты за последние пять лет [1].

Таблица 3

Страна	Золотые медали	Серебряные Медали	Бронзовые медали	Участники без медалей
Китай	22	7	1	0
Россия	16	10	4	0
США	14	11	5	0
Венгрия	14	11	5	0
Иран	11	14	5	0
Румыния	11	14	5	0
Германия	10	11	7	2
Болгария	9	17	4	0
Вьетнам	8	19	2	1
Великобритания	7	12	10	1
Украина	6	7	11	6
Ю. Корея	5	15	9	1
Франция	5	4	5	6
Япония	4	13	10	3
Канада	2	8	14	6
Тайвань	1	18	8	3

Суммарные результаты лучших команд с 1993 по 1997 г.

Для сравнения приведем таблицу 3, где представлены суммарные результаты лучших команд за период с 1993 по 1997 гг. [1].

Научный инструментарий

В целях исследования были собраны данные о студентах двух вузов со сходными характеристиками контингента, расположения и образовательного предложения. Данные содержали следующие параметры: средний балл по математике в аттестате, ЕГЭ по математике, ЕГЭ по русскому языку, общий балл ЕГЭ при поступлении в вуз и успеваемость в вузе по математике. Для указанных параметров были найдены точные и интервальные оценки коэффициентов корреляции, а также построены гистограммы частот и проверены гипотезы о нормальном распределении. Для статистических расчетов и построения гистограмм использовались формулы математической статистики и компьютерная программа для статистической обработки данных STATISTICA.

Результаты исследования

В этой статье приведены результаты исследования, проведенного в Финансово-технологической академии (ФТА) г. Королева и Российском государственном университете туризма и сервиса (РГУТиС), п. Черкизово. Были собраны данные о 104 студентах ФТА 1-го курса 2013/2014 года обучения и 290 студентах РГУТиС 1-го курса 2012/2013 года обучения, причем из последних 180 студентов с экономического факультета (ЭФ) и 110 студентов с факультета сервиса (ФС).

Для ФТА данные содержали следующие параметры: средний балл по математике в аттестате, ЕГЭ по математике, ЕГЭ по русскому языку, общий балл ЕГЭ при поступле нии в вуз и успеваемость в вузе по математике. Для РГУТиС получены данные о тех же параметрах, за исключением среднего балла по математике в аттестате.

Считаем, что данные по двум вышеуказанным вузам являются однородными и схожими по статистическим характеристикам. Основанием для этого является то, что вузы расположены территориально близко, имеют схожий набор специальностей и уровень подготовки специалистов, а студентами вузов в основном являются выпускники школ близлежащих городов и поселков Московской области.

Дополнительно были проверены на однородность данные о студентах двух разных факультетов РГУТиС: был проверен t-критерий для независимых выборок и критерий Вил-консона. Оказалось, что различия в баллах ЕГЭ по математике между факультетами ЭФ и ФС статистически не значимы. Тот же результат получен и ддя баллов ЕГЭ по русскому языку.

Ниже приведены некоторые результаты статистической обработки данных, собранных по двум вузам.

Во-первых, исследование показало крайне низкую связь между баллами ЕГЭ по математике и успеваемостью по математике в школе (по аттестату) и вузе для студентов ФТА. Ниже приведены таблицы коэффициентов корреляции [4] между этими параметрами.

Некоторыми школьными педагогами и исследователями образовательных процессов в высшей школе высказывались мнения о полном отсутствии связи между баллами ЕГЭ по математике и оценками по математике в аттестате. Более того, отмечалось, что имеется в среднем даже отрицательная связь: «чем ниже оценки в аттестате, тем выше ЕГЭ». Наше исследование

Таблица 4

Коэффициенты корреляции для ФТА

ЕГЭ по математике ЕГЭ по русскому языку Оценка по математике в аттестате Оценка по математике в вузе ЕГЭ по математике 1 ЕГЭ по русскому языку 0,33 1 Оценка по математике в аттестате 0,23 0,39 1 Оценка по математике в вузе 0,24 0,44 0,44 1 подтверждает низкую связь между оценками в аттестате по математике и ЕГЭ по математике (значение коэффициента корреляции 0,23 означает слабую зависимость).

В то же время успеваемость в вузе по математике в большей мере связана с оценками по математике в аттестате (коэффициент корреляции 0,44), чем с баллами ЕГЭ по математике (коэффициент корреляции 0,23).

Таблица коэффициентов корреляции для студентов экономического факультета РГУТиС (таблица 5) показывает более тесную связь успеваемости по математике в вузе с баллами по ЕГЭ по русскому языку (коэффициент корреляции 0,49), чем с баллами ЕГЭ по математике (коэффициент корреляции 0,36).

Аналогично таблица коэффициентов корреляции для студентов двух вузов (таблица 6) тоже показывает более тесную связь успеваемости по математике в вузе с баллами по ЕГЭ по русскому языку (коэффициент корреляции 0,41), чем с баллами ЕГЭ по математике (коэффициент корреляции 0,28).

Во всех трех таблицах прослеживается весьма любопытный парадокс: результаты ЕГЭ по русскому языку имеют гораздо более сильную линейную связь с успеваемостью в вузе по математике, чем результаты ЕГЭ по математике!

Была произведена статистическая проверка сформулированной выше гипотезы- парадокса. Результаты проверки дали возможность заключить, что указанную гипотезу следует принять с надежностью 95% для выборки ФТА (таблица 4) и с надежностью 90% для объединенной выборки (таблица 6).

Напрашивается вывод, что наличие такого противоречивого критерия, как результат ЕГЭ по математике, слабо связанный со знаниями и навыками школьников по математике, оказывает, по всей видимости, отрицательное влияние на систему математического образования в стране.

Посмотрим теперь на частоты баллов ЕГЭ. По законам математической статистики, график этих частот (гистограмма) должен быть близок к так называемому нормальному закону распределения [4]. Например, для ЕГЭ по русскому языку по результатам исследования получаются следующие гистограммы (рис. 1, 2), соответственно для 104 студентов ФТА и 394 студентов двух вузов. Можно отметить некоторое сходство графика частот на обеих гистограммах с приведенными кривыми нормального распределения.

Вместе с тем неоднократно приходилось слышать мнение, что результаты ЕГЭ по математике не подчиняются законам статистики. Это говорит о существенном влиянии на результаты ЕГЭ по математике факторов, не имеющих природу случайных отклонений. Результаты проведенного исследования подтверждают такое мнение.

Таблица 5

Коэффициенты корреляции для экономического факультета РГУТиС

	ЕГЭ по математике	ЕГЭ по русскому языку	Оценка по математике в вузе
ЕГЭ по математике	1
ЕГЭ по русскому языку	0,66	1
Оценка по математике в ВУЗе	0,36	0,49	1

Таблица 6

Коэффициенты корреляции для РГУТиС и ФТА

	ЕГЭ по математике	ЕГЭ по русскому языку	Оценка по математике в вузе
ЕГЭ по математике	1
ЕГЭ по русскому языку	0,54	1
Оценка по математике в вузе	0,28	0,41	1

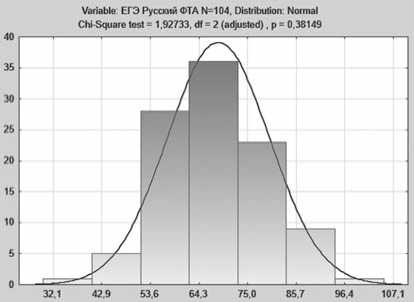
Рис. 1. Гистограмма распределения частот результатов ЕГЭ по русскому языку ФТА

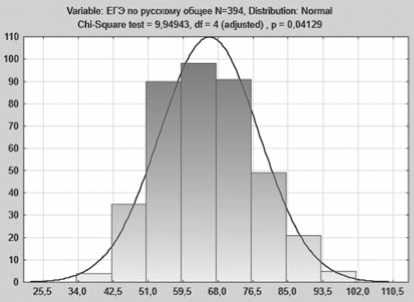
Рис. 2. Гистограмма распределения частот результатов ЕГЭ по русскому языку ФТА и РГУТиС

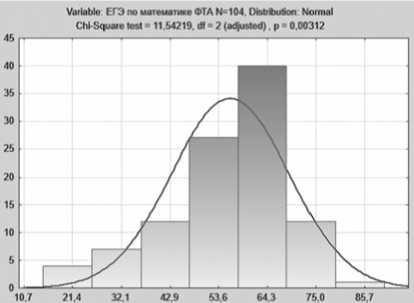
Рис. 3. Гистограмма распределения частот результатов ЕГЭ по математике ФТА

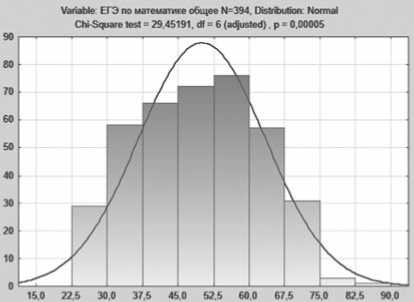
Рис. 4. Гистограмма распределения частот результатов ЕГЭ по математике ФТА и РГУТиС.

Ниже приведены две гистограммы частот баллов ЕГЭ по математике, первая — для студентов ФТА (рис. 3), вторая — для студентов двух вузов (рис. 4). Обе они имеют значительные, заметные даже на глаз, отклонения от кривой нормального распределения. Методы статистики (критерий «хи-квадрат» Пирсона) [2] подтверждают, что отклонение частот существенно.

Выявлено также достаточно сильное изменение студентами ФТА своих оценок по математике в вузе по сравнению со школьными оценками (как в лучшую, так и в худшую сторону). Ниже (рис. 5) приведены частоты среднего балла по математике в аттестате (полусумма оценок по алгебре и началам анализа и геометрии) — светлые столбцы. Можно было бы ожидать, что ли-

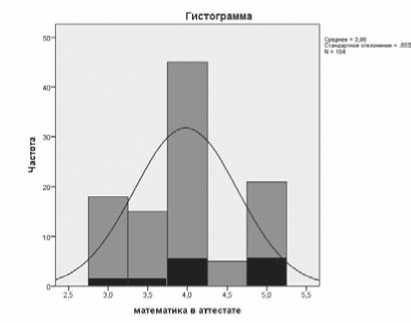
Рис. 5. Гистограмма распределения частот среднего балла по математике в аттестате ФТА

дерами групп в вузе на занятиях по математике будут студенты с высокими баллами в аттестате по этому предмету. В реальности все обстоит несколько иначе.

Если из рассматриваемых в настоящем исследовании студентов выбрать 14 лидеров по математике, по 2 лидера по математике в каждой из 7 групп студентов (темные столбцы), то это будут не только учащиеся со средним баллом 5 в аттестате. Таким образом, наблюдается появление новых лидеров по математике в вузе практически со всего спектра оценок по математике в аттестате.

Новый жизненный этап, смена обстановки и смена преподавателя дают возможность для появления новых лидеров по математике в группах студентов. Этому должна спо собствовать организация учебного процесса с уклоном на индивидуальную работу и самостоятельное выполнение заданий студентами.

Выводы. Даже небольшой объем данных в проведенном эксперименте (всего 394 студента двух вузов) позволяет сделать обоснованные выводы о проблемах, связанных с образованием в школе и вузе по математике, а именно, о проблеме малой информативности ЕГЭ по математике. Представляется важным недавнее принятие Министерством образования и науки Концепции развития математического образования. Она должна стать основным документом, по которому будет построено преподавание математики в школе и вузах.