Электромагнитные эффекты, проявляющиеся при образовании среднеширотных спорадических слоев

Проблема выяснения механизмов формирования ионосферных спорадических слоев до сих пор относится к числу нерешенных. Одна из причин этого – многофакторность задачи. Создается впечатление, что наряду с универсальными факторами, влияющими на поведение всех типов E s примерно одинаково, есть факторы, влияющие на поведение этих типов по-разному или в разной степени. Ниже мы рассмотрим некоторые аспекты зависимости спорадических слоев области Е (E s типа c , l , f ) от их положения по отношению к оси динамо-слоя [1]. Положение оси динамослоя определяется положением максимума педерсе-новской проводимости. Это условие выглядит так: ω Bi = ν in, где ω Bi – гирочастота ионов на широте наблюдения, ν in ( z m ) – частота столкновений на высоте максимума динамо-слоя z m .

Теория объясняет происхождение спорадических слоев вертикальным дрейфом ионов. Такой подход дает удовлетворительные результаты при объяснении относительно толстых слоев с «критическим» механизмом отражения, т. е. отражения сигналов от областей, где коэффициент преломления обращается в 0. Однако значительная часть E s относится к числу тонких слоев с другим механизмом отражения – отражения на резком градиенте коэффициента преломления. При этом электронная концентрация должна существенно меняться уже на длине зондирующей радиоволны. Такие образования диффузно неустойчивы. Должна существовать какая-то сила, препятствующая уменьшению градиента плазменного давления. Такой силой, как мы покажем ниже, может являться амперо-ва сила. Некоторая информация о наблюдении тонких слоев содержится в [2], где говорится об обнаружении слоев толщиной менее километра. Однако примененная методика не позволяет пока достичь большего разрешения .

Целью данной работы является обсуждение экспериментальных данных и теоретических положений относительно природы спорадических слоев с градиентным механизмом отражения.

Наблюдаемые данные и методика обработки

Исходными являлись таблицы часовых данных, снятых с ионограмм Иркутска в процессе стандартной обработки. Применялся статистический метод анализа, основными параметрами которого являлись вероятностные характеристики различных типов Es.

В качестве показателя степени связи использовался коэффициент корреляции, вычислявшийся стандартным образом. Коррелируемые ряды были получены по среднегодовым или среднесезонным значениям за период с 1960 по 1996 г.

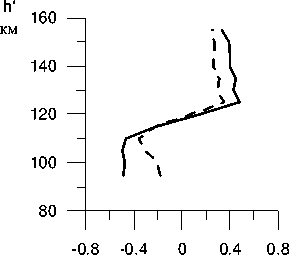
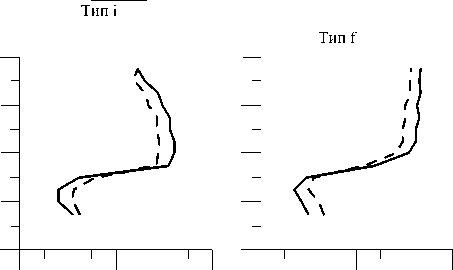
На рис. 1 изображен высотный ход коэффициентов корреляции между вероятностями появления спорадических образований данного типа и А Е - и aa -индексами магнитной активности. Отрицательная связь с магнитной активностью на высотах ниже 120 км и ее превращение в положительную при переходе через этот высотный рубеж объясняется, скорее всего, общей для всех слоев тенденцией увеличивать высоту появления с ростом магнитной активности. Немонотонность этого процесса, вероятно, связана с наличием высотного максимума в распределении плотности ионосферного тока (115–120 км).

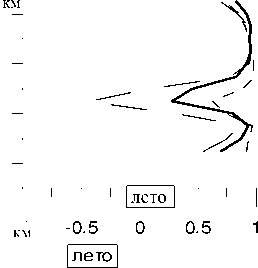
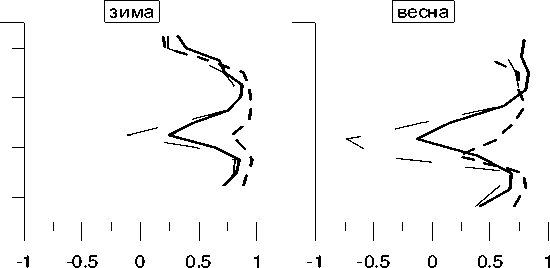
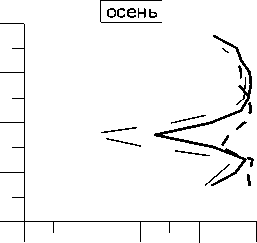
На рис. 2 изображен высотный ход корреляции между вероятностью появления слоев c и l , c и f , l и f . Видно, что при переходе через максимум токового слоя корреляция первых двух пар резко нарушается. В паре l , f этот эффект менее заметен.

Следует отметить, что как l , так и f – тонкие слои без группового запаздывания, а с – толстый слой. Конечно, условия формирования для l (дневной слой) и f (ночной) разные, но, как мы увидим ниже, их объединяет общность механизма формирования.

Теория и интерпретация

Прежде чем сделать выводы, обратим внимание на основные физические процессы и уравнения переноса простой плазмы [3].

Закон Ома j = σE связывает плотность тока с электрическим полем в тот же момент времени. Электрическое поле определяет ускорение электронов, а не их скорость, поэтому в общем случае такой связи нет. Но в таких процессах, когда все величины мало изменяются за время между столкновениями электронов с ионами, инерция электронов перестает играть роль и действие электрического поля уравновешивается при определенной величине и = ——. Это условие eN равновесия электронного газа и представляет собой закон Ома. Аналогично выглядит закон Ома для плазмы.

h' km

Тип c

среднегодовой h' 160 km

-1     -0.5    0     0.5     1

-0.8 -0.4    0    0.4   0.8   -0.8 -0.4    0    0.4   0.8

Рис . 1. Значения коэффициентов корреляции между вариациями вертикального распределения вероятностей образования различных E _s и АЕ - (сплошная кривая) и aa -индексами (штриховая линия).

c/i c/f i/f

-1     -0.5    0     0.5     1

----    ---- "c"/"l" ------------- "c"/"f"

-----"ГГГ

Рис . 2 . Высотный ход коэффициентов корреляции между вероятностями образования различных типов E _s .

Удобно выражать электрическое поле через ток, а не наоборот. Такой способ записи (кроме упрощения формул) лучше соответствует качественной картине явлений в хорошо проводящей плазме, где индуктивное сопротивление больше активного и внешние условия обычно задают именно ток, а электрическое поле определяется по закону Ома.

Относительная скорость электронов и ионов связана с плотностью тока соотношением j = – eN ( V e – V i ) = – eNu ; u = – j / eN – токовая скорость, при u = – j / eN действие электрического поля уравновешивается трением электронов об ионы. Это условие равновесия электронного газа по закону Ома. Магнитное поле влияет на трение электронов об ионы не очень сильно. Однако для протекания тока поперек магнитного поля необходима составляющая E ´ перпендикулярная току и магнитному полю, – так называемое холловское поле. Оно уравновешивает действующую на электроны силу (1/ c )[ jB ] и равно

E H = ( 1KeN e c ) ) [ JB ] = ( » e Т е /^) [ j h ] ,         (1)

где h = B/ B – единичный вектор вдоль магнитного поля, ω _е – циклотронная частота (с^–1), равная to _e = eB/m e c = 1.76 - 10⁷ B , т е - электронное время между столкновениями или время рассеяния электронов на ионах (время обмена энергиями):

3VmT2    3.5 -104 TA ee              e

--;=------ = —-----:---. 4^2nX e4 Z7   (X 10) Zn где Zni – объемный заряд ионов, λ – кулоновский логарифм.

Для столкновения частиц существенна их относительная скорость u = V_e – V . Кулоновский логарифм λ равен логарифму отношения характерного максимального и минимального параметров столкновения [3]:

^X = In ( P maxi P min ) •

С другой стороны, если сложить уравнения движения для ионов и электронов и пренебречь вязкостью и инерцией, то получается условие равновесия плазмы в виде

-V ( p e + p i ) + (V c ) [ jB ] = 0.                     (2)

Отсюда следует выражение для поперечного электрического тока:

j ± =^- eN e ( V e ^- V )_± = f c ^[ ^{h V} ( p e ⁺ P i ) J •

V B 7

По сути дела, равенство (1/ c ) [ jB ] = V ( p _e + p i ) устанавливает связь между силой Ампера и плазменным (газовым) давлением.

Для медленных процессов можно считать

Vp = (1/ c)[ jB], где р - полное давление, равное p = pe + pi, которое определяется температурой Т и концентрацией частиц N: pe = Ne Te, pi = Ni Ti.

Заменяя в (1) уравновешивающую силу (1/ c ) [ jB ] на V p , можно показать, что холловское поле E H = ( 1/ eN ) V p также связано с плазменным давлением.

Уравнение баланса электронно-ионной концентрации N в стационарном случае имеет вид дNw       ,,2

—— = q -a N ², д z

где w – скорость вертикального дрейфа плазмы относительно нейтральной атмосферы, q – плотность мощности источников ионизации, а - коэффициент диссоциативной рекомбинации. Уравнение (1) справедливо для процессов, длительность которых больше рекомбинационного времени, составляющего для ночи примерно 1000 с. Плотность вертикального потока плазмы связана с плотностью электрического тока (через силу Ампера) соотношением [3]

/ д p. [ ^jB ]

DNw = <-- 1--^;

[ д z     c

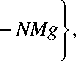
где D = з MN a V_T , M - масса «средней» молекулы атмосферы, N – плотность числа частиц атмосферы, σ – поперечное сечение столкновений ионов с молекулами воздуха, V_T – тепловая скорость молекул атмосферы.

Возможны два варианта решения уравнения (2). Статический, когда Nw = 0 в каждой точке компенсируется процессами рекомбинации согласно (1), и динамический, когда поток массы равен в среднем нулю. В последнем случае должны существовать перемежающиеся области, в которых поток попеременно направлен то вниз, то вверх так, что суммарный вертикальный поток отсутствует, а в атмосфере появляются вихри. Ионизация при этом «сгоняется» электрическим дрейфом к центру вихря. Такая ситуация многократно рассматривалась в литературе и использовалась на качественном уровне в моделях, объясняющих основные особенности Es. Однако такой подход заведомо не исчерпывает всех возможностей формирования спорадических слоев, не говоря уже об объяснении сильной зависимости поведения Es от положения и силы ионосферных динамотоков.

Далее мы будем полагать, что вертикальная компонента плотности электрического тока равна нулю:

j =a p E z +a h [ EB ] z = 0.

С учетом этого обстоятельства и того факта, что температура в интервале высот 100–130 км меняется не очень сильно (менее 5 ° на километр), (2) примет вид:

Dwz

S c [ EB ] z

c

= ( ^{д N} / ^д z ) kT ,

a где Sc = —, ос - каулинговская проводимость, рав-

(ap +aH) ная a p

.

В нашем случае выше 100 км каулинговская проводимость приближенно равна

О =« 2 NV-.

c ^,

M to2 Bi где e – заряд электрона, N – плотность числа электронов (ионов), частота столкновений ионов с нейтралами vin = 7.52aNVT, о - сечение столкновения ион-нейтрал, равное 43d0-16 см2, VT = (8kT /nMУ22 – тепловая скорость частиц атмосферы, k=1.38 10–16 эрг/градус, – постоянная Больцмана, T – кинетическая температура ионов (нейтралов), юв. - гирочастота ионов, равная на широте Иркутска 190.5 с–1.

Для дальнейшего (5) удобно представить в виде

1 f dN ) f D )    f S„ )[ ^EB J

=

N V dz ) V kT ) z V kT ) c

или в численном виде

—f dN) = 1.5-10-20N Гw7 -1.11-104a 1,(7)

N V dz )             L z где wz – скорость вертикального движения ионосферной плазмы относительно нейтральной атмосферы в см/c, а – напряженность горизонтальной составляющей электрического поля Е в единицах мВ/м.

Фактически (4) описывает два процесса, идущих в противоположных направлениях. Амперова сила формирует градиент газового давления (в нашем случае dN / dz ), а диффузия, описываемая членом ( D/kT ) w z , стремится этот градиент уничтожить.

Уравнение (4) описывает случай равновесия этих процессов. Подробные экспериментальные исследования спорадических слоев, проведенные с помощью нового метода диагностики, основанного на измерениях параметров ионосферы с помощью искусственных периодических неоднородностей, возбуждаемых в плазме мощной стоячей радиоволной [2], показали, что спорадические слои представляют собой резкие градиенты электронной концентрации небольшой вертикальной протяженности (всего несколько длин волн) с характерными скоростями движения плазмы в единицы метров в секунду (чаще 1–3 м/c). Таким образом, это тонкие слои, к описанию которых приходится привлекать точные решения волнового уравнения, так как приближение геометрической оптики здесь неприменимо. Поскольку точное распределение электронной концентрации внутри такого слоя нам не известно, да и не представляет интереса в данном случае , мы ограничимся применением простейшей модели так называемого переходного слоя [4]. Для этой модели координатная зависимость коэффициента преломления задается в виде

n

= 1 —

Kemz

I + e^mz ) "

Здесь K – постоянная, определяемая из граничного условия.

Допустим, что перед слоем ( z =0) n (0)= n 0 , а далеко за слоем, при z →∞, соответственно n ∞ . Тогда

( 1 + n ~ )

K = 1 — nи n02 = —2—, а для коэффициента от- ражения переходного слоя существует выражение для случая нормального падения, имеющее вид [4]

sh [ 0.5 л 5 (1 — n „ ) ]

R Г                  1 , sh [ 0.5л S (1 + n„)]

где S – мощность переходного слоя, выраженная в длинах волн.

Для случая, когда пS(1 — nw) > 1, формула (8) пе реходит в

R = exp ( —п Sn „ ) ,

при этом n _∞→0 по мере того, как зондирующая частота приближается к критической.

Сформулируем теперь условия наблюдаемости Es. Очевидно , что если в распределении электронной плотности достигается условие n = 0, то такой слой будет иметь R = 1. Если же критическая плотность нигде не достигается, то величина πSn∞ может быть мала из-за небольшой S. Это как раз тот случай, когда возникает резкий градиент электронной кон-2k центрации. По определению S = —0.

m

C другой стороны, из рис. 3 cледует, что

*

— ~ 0.3 - 2. 4 п

Тогда

„ = 1.67 z *

X 0   , где z* следует рассматривать как полутолщину слоя:

f dN ^—1

z* = n II . Чтобы коэффициент отражения был

V dz )

не слишком малым в условиях, когда частота зондирующего сигнала далека от критической ( n ₀ ~ 0.5), необходимо, чтобы показатель в (9) был не меньше –2.3, что соответствует условию R >  0.1. Тогда на величину относительного градиента накладывается условие

1 f dn n V dz

2 24

> — = 7.46 - 10 ^{— 4} b , X 0

где b – частота зондирующего сигнала в МГц. Подставив (10) в (7), мы получим условие наблюдаемости отраженного сигнала на частоте b :

b <  2 - 10"¹⁷ [ w z — 1.11 - 10⁴ a ] N . (11)

На автоматических станциях ионосферного зондирования минимальная излучаемая частота обычно равна 1 МГц. Тогда условие наблюдаемости (11) перепишется в виде

N >  5 - 10¹⁶ _[ w_z + 1.11 - 10⁴ | a |_] "'. (12)

Очевидно, что при а = 10, т. е. при напряженности электрического поля в 10 мВ/м, отражающие слои могут наблюдаться во всем диапазоне Е s -области от 100 до 130 км как днем, так и ночью. С уменьшением напряженности поля условия наблюдения ухудшаются. Наконец, при а ~ 10^-4 w_z диффузия, разрушающая тонкий слой, становится столь сильна, что формирование слоев становится неэффективным. Впрочем, это происходит при довольно низких значениях поля, меньших (4–6)·10^–2 мВ/м. Рекомбинация «съедает» дополнительную ионизацию, поэтому уравнение (3) также нужно учитывать. Однако для тонких слоев с относительно малой электронной концентрацией этот эффект будет незначительным.

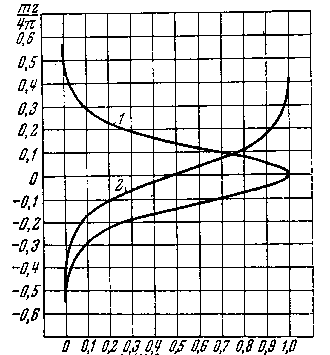
Рис . 3. Формы симметричного и переходного слоев : 1 – кривая для симметричного слоя, 2 – кривая для переходного слоя.

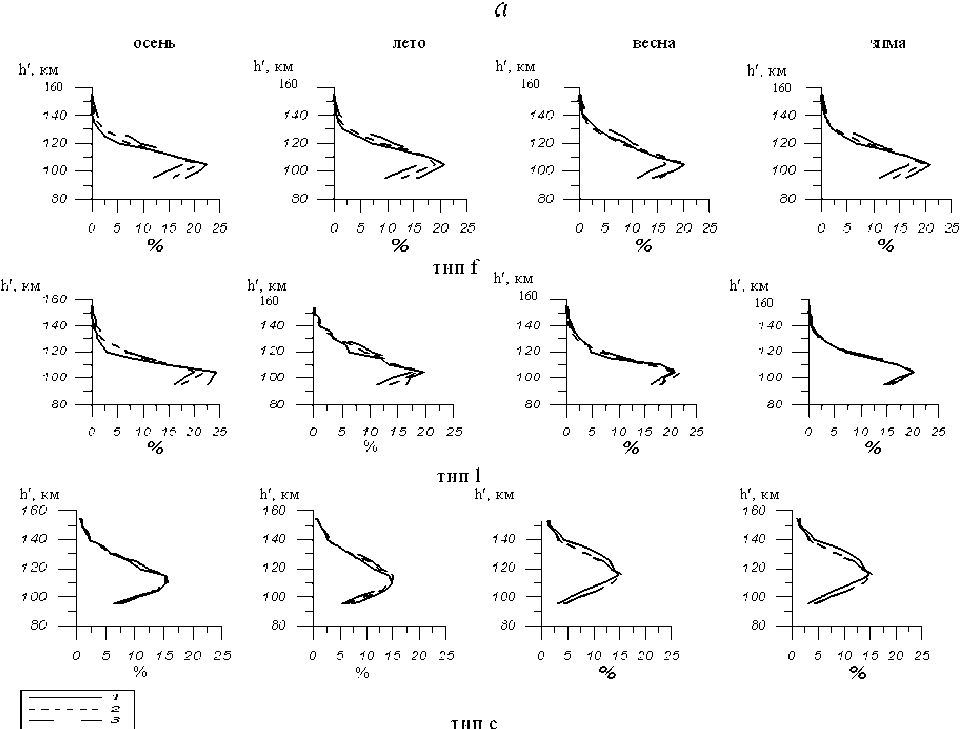
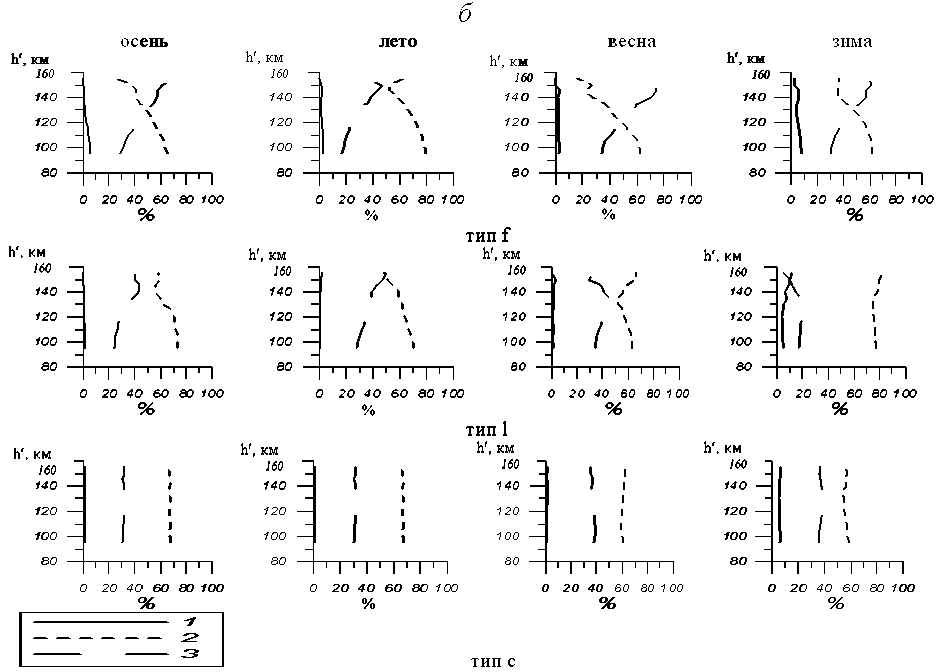
Рис. 4. Распределение вероятностей образования различных типов E _s по высотам в зависимости от к -индекса: к =0^1 (кривые 1 ), к =2^3 (кривые 2 ), к >3 (кривые 3 ). Случаи а, б относятся к разным методам нормировки параметров вероятностей образования различных типов E _s (см. текст).

Особо подчеркнем, что механизм образования тонких слоев не зависит от величины фоновой электронной концентрации и работает как днем, так и ночью.

Рассмотрим распределение вероятности образования различных типов Е s на разных высотах в зависимости от разных уровней геомагнитной активности ( k ), полученных на ст. Иркутск. Значение k = 0÷1 относилось к слабой, k = 2÷3 – к умеренной и k >3 – к сильной активности. На рис. 4 показано вертикальное распределение вероятности образования в зависимости от трех уровней геомагнитной активности. Рассматривалось два метода нормировки параметров вероятностей образования. В первом (рис. 4, а) бралось за 100 % суммарное вертикальное распределение для каждого уровня геомагнитной активности отдельно. Во втором случае (рис. 4, б) на каждом уровне высот за 100 % принималось суммарное количество образований E s независимо от уровней геомагнитной активности. Общей закономерностью всех типов E s является то, что максимумы в вертикальном распределении вероятности образования практически остаются на одном и том же уровне высот и мало зависят от уровней геомагнитной активности. Эти максимумы совпадают с максимумами холловской и педерсеновской проводимостей. Однако при рассмотрении каждого уровня высот оказывается, что в большинстве случаев увеличение геомагнитной активности приводит к увеличению вероятности образования на больших высотах и снижению на малых, аналогично поведению коэффициентов корреляции, показанных на рис. 1. Следует отметить, что реакция на изменение геомагнитной активности у E s типа с выражена гораздо слабее по сравнению с E_s типа l и f .

Заключение

Из сказанного выше следует, что различие в реакции слоев l и f , с одной стороны, и с – с другой, на плотности электрического тока связано с различным происхождением этих слоев.

Слои l и f возникают там, где плотность тока такова, что возникающий градиент давления и, соответственно, плотности плазмы создает тонкий слой с коэффициентом отражения, достаточным для получения отраженного сигнала измеримой амплитуды. Слой c возникает там, где плазма достигает критической плотности, т. е. где коэффициент преломления обращается в нуль. В средних широтах это возможно практически лишь в светлое время суток. В отличие от напряженности горизонтальной составляющей электрического поля, которая меняется во всем интервале ионосферных высот в несколько раз, составляющая плотности ионосферного тока меняется в этом же интервале высот в несколько десятков раз. Там, где ток максимален, максимальны и связанные с ним градиенты (2). При этом возникает своеобразная конкуренция. В области повышенных градиентов «стягиваются» электрические токи. Их плотность, следовательно, уменьшается в других местах динамо-слоя. Уменьшаются и возможности образования второго Es. Из условия (10) следует, что область максимального значения ионосферных токов территориально полностью совпадает с областью локализации Es.

С ростом геомагнитной активности увеличивается количество образований E s выше уровня высот максимальной холловской и педерсеновской проводимостей и снижается ниже этих уровней. Независимо от геомагнитной активности уровни высот максимумов в вертикальном распределении вероятностей образования E s практически не меняются и зависят только от сезона.