Компетентностно ориентированные технологии на уроках математики

Под компетентностно ориентированным обучением в системе среднего профессионального образования понимаются такие подходы к обучению, которые целенаправленно способствуют формированию у студентов общих и профессиональных компетенций посредством включения их в учебно-профессиональную деятельность [1]. В этой связи педагогу необходимо предусматривать использование в образовательном процессе активных и интерактивных форм проведения уроков в сочетании с внеаудиторной работой.

Анализ теоретических исследований и педагогической практики позволяет нам к эффективным технологиям формирования общих и профессиональных компетенций студентов отнести:

– технологию проблемно-деятельностного обучения;

– технологию «Мозговой штурм»;

– технологию развития критического мышления через чтение и письмо (ТРКМЧП);

– кейс-технологии;

– технологию витагенного обучения;

– технологию проектно-исследовательской деятельности.

Рассмотрим примеры использования этих технологий на уроках математики.

Технология проблемного обучения.

Проблемное обучение — это такая форма организации учебного занятия, при которой предполагается создание под руководством педагога проблемных ситуаций и активная са- мостоятельная деятельность студентов по их разрешению. В результате такой организации занятий студент овладевает профессиональными знаниями, навыками, умениями, развивает творческие и мыслительные способности [2].

Примеры проблемных задач.

Задача № 1. Длина цистерны для перевозки дизтоплива 4 м, диаметр 2 м. Сколько топлива надо влить в цистерну, чтобы заполнить ее на 3/4 объема?

Студентам еще пока не знакомы понятие объема цилиндра и формула для его нахождения. Они находят необходимую информацию, используя текст учебника, обсуждают решение задачи, делают выводы.

Задача № 2. При проектировании и изготовлении различного вида емкостей для хранения и перевозки газов, жидкостей, сыпучих материалов изготовитель стремится получить максимальный объем изделия, но при этом площадь поверхности должна быть минимальна, расход материала более экономичен и рационален.

В наличии имеется стальной лист толщиной 5 мм, шириной 2 м и длиной 3 м. Необходимо из него изготовить емкость для перевозки жидкости максимального объема, оптимальной формы, с минимальной трудоемкостью изготовления.

При таких условиях предполагаем, что возможно изготовление емкости либо в виде цилиндра, либо в форме параллелепипеда.

Далее определяем размеры емкости в каждом случае и составляем функцию для решения задачи. Исследуем ее на наибольшее значение с помощью производной и делаем вывод.

Задача № 3. Вспомните, в каких случаях на производственной практике вам приходилось сталкиваться с проблемой измерения угла между двумя пересекающимися плоскостями, между двумя скрещивающимися прямыми? Приведите пример измерения таких углов при выполнении производственной операции.

Задача № 4. Станочнику необходимо рассчитать, как будет выглядеть сосуд, полученный вращением графика функции у = х² + 1 вокруг оси ОХ, найти объем этого сосуда.

Целесообразно ли его изготавливать, если в этот сосуд должно помещаться 100 см3?

Данная технология позволяет:

– активизировать познавательную деятельность студентов на уроке;

– научиться получать новые знания из разных источников информации;

– сформировать стойкую учебную мотивацию;

– применять полученные навыки организации самостоятельной работы;

– повысить самооценку студента, так как при решении проблемы учитываются и принимаются во внимание различные мнения.

Технология «Мозговой штурм».

Мозговой штурм представляет собой свободный обмен мнениями, который включает студентов в процесс общения, способствует реализации их творческого потенциала и приобщает к активному поиску решений поставленной проблемы.

Мозговой штурм ведет специально подготовленный человек (модератор). Его задача — подстегивать и контролировать процесс выдвижения идей, поддерживать его непрерывность. Модератор способствует формированию у студентов уверенности в возможности преодоления проблемы. При этом он не должен оказывать сильного давления на участников.

Мозговой штурм состоит обычно из трех этапов:

– постановка проблемы;

– генерация идей;

– отбор, систематизация и оценка идей.

Пример занятия с использованием технологии «Мозговой штурм».

Тема «Методы решения логарифмических уравнений».

До проведения учебного мозгового штурма были изучены свойства логарифмической функции, свойства логарифмов и простейшие методы решения логарифмических уравнений, основанные на применении этих свойств. Задача мозгового штурма — открытие других методов решения логарифмических уравнений.

Урок начинается с актуализации имеющихся у студентов знаний. Студенты отвечают на следующие вопросы.

– Какими свойствами обладает логарифмическая функция?

– Какие свойства логарифмов вы знаете?

– Какие методы решения логарифмических уравнений вам уже известны?

Применяя эти методы, устно разбираем решение нескольких уравнений. Далее учебный мозговой штурм строится в соответствии со следующим алгоритмом:

– студенты выбирают один из новых типов уравнений;

– 5–10 минут работают в группах;

– выдвигают и обсуждают новые идеи;

– реализуют свои идеи, решая одно из уравнений у доски;

– анализируют и корректируют решения.

Первый этап учебного мозгового штурма: выделение групп однотипных уравнений; формулировка отличительных признаков.

Студенты работают в группах. Им необходимо выделить 3–4 группы уравнений, которые объединены какой-либо особенностью. Студенты используют имеющиеся на столах карточки с уравнениями, раскладывая их в отдельные группы. Преподаватель наблюдает за работой, затем результат обсуждается и корректируется другими группами. Далее для каждого столбика уравнений творческая группа формулирует отличительный признак и выделяет наиболее простое уравнение, которое и будет впоследствии решаться.

Второй этап учебного мозгового штурма: генерирование идей об оптимальном методерешения уравнений отдельных групп.

Для каждого типа уравнений группа должна найти оптимальный способ решения, используя при этом наиболее общие методы решения уравнений. На этом этапе не нужно торопить студентов, нельзя отвергать ни одной идеи и навязывать им свои методы, можно лишь подсказывать направления поиска, поддерживать творческую атмосферу. При этом поощряется каждая идея на пути поиска, а ошибки анализируются.

И, наконец, третий этап учебного мозгового штурма: анализ идей, коррекция, выводы.

Студенты формулируют полученные методы решения для рассмотренных типов уравнений.

Технология развития критического мышления через чтение и письмо.

Данная образовательная технология направлена на развитие стиля мышления студентов, основными чертами которого являются критичность, открытость, гибкость, рефлексивность, посредством чтения и письма [3].

Примеры основных приемов технологии развития критического мышления через чтение и письмо на уроках математики.

Прием «Кластер».

Понятие «кластер» переводится как «гроздь, пучок». Суть приема в том, чтобы представить информацию в графическом виде. В центре записывается ключевое понятие, рядом указываются понятия второго уровня, связанные с ключевым, и соединяются с ним линиями или стрелками. Этот прием может быть использован на любой стадии урока.

Использование кластера способствует как систематизации материала, так и установлению причинно-следственных связей между элементами. Заданием может стать и укрупнение одного или нескольких элементов, выделение новых.

Пример кластера по теме «Геометрические тела» (рис. 1).

Прием «Верные и неверные утверждения», или «Верите ли вы?».

Студенты, выбирая верные утверждения из предложенных преподавателем, описывают заданную тему. Например, верно ли, что:

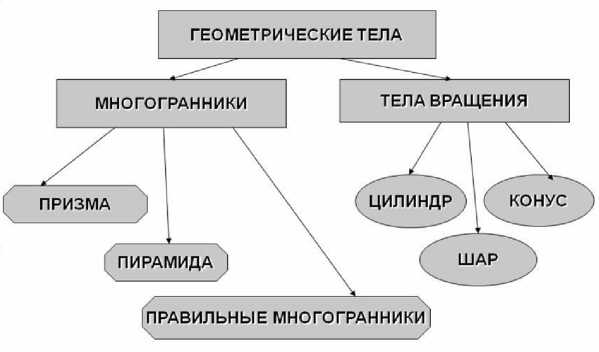
Рис. 1. Кластер «Геометрические тела»

– высота пирамиды равна ее боковому ребру;

– все грани пирамиды могут быть равными фигурами;

– высота конуса — это любой отрезок, проведенный из его вершины к основанию;

– площадь полной поверхности цилиндра состоит из площади боковой поверхности и площади основания;

– два параллелепипеда имеют равные объемы, если равны их стороны основания;

– только одна грань прямой призмы перпендикулярна к плоскости ее основания;

– осевое сечение конуса — это треугольник;

– цилиндр образован вращением прямоугольного треугольника вокруг катета;

– у шара есть боковая поверхность;

– сечением шара плоскостью является круг.

Прием «Кубик».

Данный прием удобно использовать на этапе осмысления. Он позволяет студентам рассмотреть проблему или тему под разными углами, создает на уроке целостное представление об изучаемом материале, способствует правильной интерпретации полученной информации.

Студенты делятся на группы. Преподаватель над каждым столом бросает кубик, на гранях которого написаны вопросы по теме, начинающиеся со слов «почему», «назови», «объясни», «предложи», «поделись», «придумай». Таким образом определяется, в каком ракурсе будет группа осмыслять ту или иную тему занятия.

Например, при изучении темы «Тригонометрические функции» студентам могут быть предложены следующие вопросы и задания, расположенные на гранях кубика.

– Почему уравнение sin x = 2 не имеет корней?

– Назови основное тригонометрическое тождество.

– Объясни , как называется часть окружности, ограниченная двумя координатными прямыми.

– Предложи несколько способов преобразования тригонометрического выражения.

• -    Поделись известными тебе способами решения тригонометрических уравнений.

• -    Придумай тригонометрическую функцию, график которой растянется вдоль оси ОУ и сместится влево вдоль оси ОХ.

Прием «Исправляем ошибки».

Студентам необходимо найти ошибки в решении предложенной задачи, например, такой.

Дано: KABCD — пирамида, AB = BC = 12; h = 10.

Найти: S_полн.

Решение:

S

полн.

S бок.

+ 2S , осн.

S бок.

= 1/2 P

осн.

×∙H;

Pосн. = 4АВ = 4 × 12 = 48.

Из треугольника KOM по теореме Пифагора KO2 = KM2 - OM2 = 102 - 62 = 100 — 36 = 64, H = 8;

Sбок. = 1/2 × 48 × 8 = 192; Sосн. = 122 = 144;

Sполн. = 192 + 2 × 144 = 480.

Ответ: S_полн = 480.

Прием «Концептуальная таблица».

Применяется при изучении тем, в которых можно сравнить несколько объектов. Студенты фиксируют свои выводы, дополняют, исправляют и сравнивают информацию.

Например, при изучении темы «Показательная и логарифмическая функции» может быть использована такая таблица (табл. 1).

Таблица 1

Вид функции	Область определения	Область значений	Возрастание и убывание	Четность/ нечетность	Нули функции
Показательная функция
Логарифмическая функция

Кейс-технология.

Кейс-метод — это метод активного обучения на основе реальных ситуаций. Цель этого метода состоит в формировании интереса и позитивной мотивации студентов, обеспечении их эмоциональной включенности в учебный процесс [4].

Последовательность работы при использовании кейс-метода:

• –    ознакомление с задачей;

• –    формирование целей;

• –    построение модели реальной ситуации;

• –    сбор информации по кейс-задаче;

• –    принятие решений;

• –    рассмотрение альтернатив и сравнительный анализ;

• –    презентация решений.

При использовании на занятии данной технологии происходит формирование у студентов следующих компетенций, включающих в себя способность:

• –    осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач;

• – работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями;

  – принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

Пример кейса при изучении темы «Площадь боковой и полной поверхности призмы». Вид кейса: практический.

Студентам предлагается обсчитать стоимость ремонта в автомастерской, состоящей из трех помещений.

Для решения поставленной задачи необходимо ознакомиться с прайс-листами трех фирм и выбрать самый оптимальный вариант по закупке строительного материала и найму рабочих.

Группам предлагаются следующие задания.

Группа 1. Проанализировать прайс-лист цен магазина «Уют». Произвести вычисления для проведения ремонта первого помещения и оплаты труда рабочим.

Группа 2. Проанализировать прайс-лист цен магазина «Хозяин». Произвести вычисления для проведения ремонта второго помещения и оплаты труда рабочих.

Группа 3. Проанализировать прайс-лист магазина «Самоделкин». Произвести вычисления для проведения ремонта третьего помещения и оплаты труда рабочих.

Содержание кейса.

Цель: произвести ремонтные работы в автомастерской.

Виды работ: выровнять стены, выложить пол плиткой, отремонтировать потолок в каждом помещении. Отделочные материалы выбрать в одном из трех предлагаемых магазинов, исходя из наиболее экономичного варианта стоимости материала. Для проведения отделочных работ выбрать наиболее экономически выгодную бригаду и рассчитать стоимость самого выгодного варианта.

Размеры автомастерской:

– первое помещение: 6×7×4 м, имеется окно, ширина которого 1,5 м и высота 2 м, расположенное в стене с меньшими размерами; напротив окна находится дверь высотой 2 м и шириной 1,2 м;

– второе помещение: 5×9×4 м, имеется 2 окна шириной 1,5 м и высотой 2 м, располо- женные в стене с большими размерами; напротив окон находится дверь высотой 2 м и шириной 1,2 м;

– третье помещение: 8×8×4 м, имеется окно, длина которого 1,5 м и высота 2 м, расположенное в стене с меньшими размерами; напротив окна находится дверь высотой 2 м и шириной 1,2 м.

Студенты определяются с наиболее экономичным прейскурантом стоимости услуг и материалов, заполняют таблицы (табл. 2, 3).

Отчет о выполнении заданий студенты представляют в виде итоговой таблицы и объясняют, как проводили расчеты (табл. 4).

Таблица 2

Наименование работ	Цена за 1 м2
Шпатлевка и выравнивание стен
Покрытие пола плиткой
Ремонт потолка

Таблица 3

Наименование материала	Цена
Плитка для пола
Штукатурка
Потолочная плитка

Таблица 4

	Площадь первого помещения (м2)	Площадь второго помещения (м2)	Площадь третьего помещения (м2)	Площадь общая (м2)	Расход материалов	Стоимость материалов	Стоимость работ
Штукатуры
Маляры
Отделка потолков и пола

Вопросы для обсуждения.

– С какой темой вы сегодня познакомились?

– Каким практическим навыкам вы научились?

– Какие математические знания вам помогли на уроке?

Результатом кейса является оптимальный выбор магазина строительных материалов и найма рабочей бригады для проведения ремонтных работ в автомастерской.

Технология витагенного обучения.

Витагенное обучение — это обучение, которое основано на актуализации жизненного опыта личности, ее интеллектуально-психоло- гического потенциала в образовательных целях. Витагенная технология, в отличие от других, рассматривает жизненный опыт как основу для формирования личности. Суть технологии заключается в том, чтобы выяснить, каким запасом знаний обладают студенты, перед тем как предлагать им новые знания. Данная технология позволяет определить интеллектуальный потенциал как отдельных студентов, так и коллектива в целом, создает психологическую установку на успешное получение новой информации, дает возможность использовать уже имеющуюся информацию при решении проблемных ситуаций [5].

Реализация технологии витагенного обучения позволяет:

– создавать ситуацию успеха у студентов;

– развивать познавательный интерес;

– воспитывать коммуникативную культуру;

– формировать адекватную оценку;

– придавать активный и целенаправленный характер деятельности студентов, создавать у них привычку пристально вглядываться в жизнь, накапливать знания «про запас»;

– учитывать жизненный опыт студента с его уникальностью, личностной значимостью;

– формировать умения и навыки глубокого анализа жизненных ситуаций на основе конкретного опыта обучающегося, а не абстрактных рассуждений.

В качестве примера приведем фрагмент урока по теме «Конус», который является первым уроком этой темы.

Преподаватель: предметом изучения на нашем уроке будет такое тело (демонстрируется модель конуса). Как вы думаете, как называется такое тело?

Студенты: конус.

Преподаватель: что вы о нем знаете? (каждый студент по порядку называет что-то, касающееся конуса, опираясь на свой жизненный опыт).

Студенты приводят разные аргументы: из чего состоит, где встречается, форма конуса, какие формы еще можно встретить.

Далее строим изображение конуса, разбираем алгоритм его построения, с учетом высказываний студентов даем определение конуса и его элементов, разбираем различные виды сечений.

Технология проектно-исследовательской деятельности.

С 2015 года в учебных планах предусмотрена обязательная реализация индивидуального проекта по одной из общеобразовательных дисциплин, в связи с чем технология проектно-исследовательской деятельности становится еще более актуальной [6].

Проектно-исследовательская деятельность — это технология, основанная на научном методе познания, которая предполагает решение студентами разнообразных задач исследовательско-творческого характера под руководством педагога.

Этапы:

– анализ проблемы (определение проблемы и вытекающих из нее задач исследования);

– постановка цели (выдвижение гипотезы, обсуждение методов исследования);

– поиск и обработка информации, ее анализ и синтез (сбор, систематизация и анализ полученных данных);

– оценка полученных результатов и выводов (подведение итогов, оформление результатов, их презентация);

– выводы, выдвижение новых проблем исследования.

Формы работы: индивидуальная; парная; групповая, коллективная.

Пример исследовательского проекта по математике студента, обучающегося по специальности «техническое обслуживание и ремонт автомобильного транспорта».

Тема проекта «Магия тел вращения».

Форма: индивидуальная.

Цель исследования: исследование значимости тел вращения в нашей жизни и в специальности «техническое обслуживание и ремонт автомобильного транспорта», их неоспоримого многообразия, красоты и изящества.

Задачи исследования:

– собрать иллюстративный материал по теме «Тела вращения и их виды» и систематизировать знания об основных видах тел вращения;

– проследить историю изучения видов тел вращения;

– определить возможности применения тел вращения в разных сферах человеческой деятельности;

– найти и систематизировать информацию о применении тел вращения в специальности «техническое обслуживание и ремонт автомобильного транспорта» и составить задачи практической направленности для применения на уроках математики.

Объект исследования: тела вращения.

Предмет исследования: применение тел вращения в различных сферах человеческой деятельности.

Методы исследования: анализ литературы, сбор информации, описание, систематизация и обобщение.

СОДЕРЖАНИЕ

Введение

• 1.    Тело вращения, как геометрическая фигура

• 2.    История изучения тел вращения

• 3.    Области применения тел вращения

  • 3.1.    Тела вращения в архитектуре

  • 3.2.    Тела вращения в биологии и химии

  • 3.3.    Тела вращения в природе

  • 3.4.    Тела вращения в повседневной жизни

• 4.    Тела вращения в моей специальности

  • 4.1.    Виды деятельности специалиста по техническому обслуживанию и ремонту автомобильного транспорта

  • 4.2.    Области автомобиля, где пригодятся знания по теме «Тела вращения»

  • 4.3.    Примеры тел вращения в специальности

  • 4.4.    Задачи практической направленности по теме «Тела вращения»

Заключение