Компьютерная анимация на уроках алгебры в 7-х классах: результаты экспериментальной работы
Автор: Сарыглар Сайдыс Васильевна
Журнал: Вестник Красноярского государственного педагогического университета им. В.П. Астафьева @vestnik-kspu
Рубрика: Научный дебют
Статья в выпуске: 4 (58), 2021 года.
Бесплатный доступ
Проблема и цель. В статье рассматривается проблема визуализации в обучении математике с использованием анимационных рисунков. Цель статьи - представить анализ экспериментальной работы по реализации компьютерной анимации в среде GeoGebra как средства повышения качества подготовки по алгебре учащихся 7-х классов. Методология исследования. Методологические основы исследования составили деятельностный, информационный и наглядный подходы к обучению математике, обобщение опыта работы автора статьи по апробации компьютерной анимации в школе. Результаты. Результаты экспериментальной работы подтвердили целесообразность использования компьютерной анимации в процессе обучения алгебре в 7-м классе (повысились учебная активность учащихся, интерес к исследовательской работе и качество освоения математических знаний и умений). Заключение. Применение компьютерной анимации на уроках математики в школе повышает уровень понимания и усвоения математических знаний благодаря обеспечению наглядности математических понятий и утверждений. Анализ экспериментальной работы показал возможности компьютерных сред в расширении технологической оснащенности современного учителя математики для достижения более высоких образовательных результатов.
Компьютерная анимация, анимационный рисунок, среда geogebra, эксперимент, алгебра, 7-й класс
Короткий адрес: https://sciup.org/144162143
IDR: 144162143 | УДК: 373.41 | DOI: 10.25146/1995-0861-2021-58-4-310
Текст научной статьи Компьютерная анимация на уроках алгебры в 7-х классах: результаты экспериментальной работы
DOI:
Постановка проблемы. Согласно ФГОС среднего (полного) общего образования необходимость овладения информационными технологиями в процессе изучения предметной области «Математика и информатика» определена следующими требованиями к предметным результатам освоения базового курса математики: использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; владение навыками использования готовых компьютерных программ при решении задач; сформированность представлений о компьютерно-математических моделях и необходимости анализа соответствия мо- дели и моделируемого объекта. Эти требования актуализировали проблему эффективного использования в процессе обучения различных цифровых средств и технологий.
Методология исследования базируется на деятельностном, информационном и наглядном подходах к обучению математике, обобщении опыта работы, использовании метода эксперимента и математических методах обработки результатов экспериментальной работы.
Обзор научной литературы. Различные аспекты использования цифровых средств обучения математике на различных уровнях образования в последние годы изучаются многими отечественными и зарубежными авторами.
Е.Ы. Бидайбеков, Т.С. Зимнякова, Т.О. Кочеткова, С.В. Ларин, В.Р. Майер, С. Гарнер (S. Garner), С. Гроздев (S. Grozdev), Е. Сеховик (E. Sehovic), М. Томас (M. Thomas) и др. в своих работах исследовали специфику использования цифровых средств, в том числе и анимационных.
Особенности мультимедийных средств обучения математике и информатике в условиях реализации системно-деятельностного подхода рассматривались П.С. Ломаско, А.Л. Симоновой, С.В. Чилбак-оол, К. Хирш (C. Hirsch), Б. Крамарски (B. Kramarski) и др.
Методики создания и использования компьютерной анимации в среде GeoGebra при обучении математике описаны в работах С.В. Ларина, Е.В. Казаковой, Е.А. Сивухиной, С.В. Чилбак-оол и др.
Анимационные рисунки позволяют внести движение в преподавание математики. Анимационный рисунок целесообразно применять в качестве живого плаката для создания иллюстраций фактов и рассуждений либо как виртуальный инструмент, как виртуальную лабораторию, позволяющую проводить математические эксперименты, исследовать математические ситуации. Анимационные рисунки (динамические чертежи) открывают новые возможности для развития умений анализировать чертеж, находить связи между его элементами, вносить в чертеж новые элементы – дополнительные построения, которые выявляют такие связи.
Анимационные рисунки могут быть использованы на уроке, учитель может задействовать их в видеоуроке, мультимедийном пособии, анимационными рисунками можно обмениваться с учениками и преобразовывать их онлайн. Примеры анимационных рисунков можно найти в работах [Абдулкин и др., 2019; Би-дайбеков и др., 2019; Ларин, 2015].
Результаты исследования. Эксперимент по использованию анимационных рисунков на уроках алгебры имел своей главной целью проверку эффективности разработанной технологии использования анимационных рисунков учащихся основной школы в динамической среде GeoGebra.
Экспериментальное исследование состояло из трех этапов и проводилось в течение трех лет (2016–2019).
Подготовительный этап (2016–2017 уч. год) был направлен на изучение специальной литературы, разработку уроков с использованием анимационных возможностей в среде GeoGebra, определение выборки обучающихся.
Формирующий этап (2017–2018 уч. год) – проведение уроков алгебры в 7-м классе на основе созданных разработок.
Обобщающий этап (2018–2019 уч. год) подтверждает справедливость гипотезы о том, что использование компьютерной анимации в среде GeoGebra служит как средство повышения качества математической подготовки школьников.
В качестве экспериментальной базы на всех этапах выступала МБОУ «Гимназия № 5» г. Кызыла (общее количество испытуемых составили 50 учащихся).
Экспериментальное обучение проводилось в течение 18 часов в экспериментальном классе.
Приведем результаты некоторых наблюдений за всей работой, а также результаты эксперимента. Контрольные срезы и тестирование для школьников, проводимые в 7-х классах, показали, что использование компьютерной среды GeoGebra повышает мотивацию и интерес при изучении алгебры. Некоторым показателем эффективности предлагаемой методической системы могут служить контрольные работы по темам. Для повышения объективности в обоих классах давались одинаковые контрольные работы по структуре и содержанию. Работа состояла из пяти заданий, которые проверяют знания учащихся по теме «Многочлены». Результаты выполнения контрольной работы, представленные на рис. 1, подтверждают наше предположение о повышении уровня усвоения математических знаний и умений в экспериментальных классах, обнаруживается некоторое их повышение в том классе, где была изучена тема с помощью компьютерной среды GeoGebra [Grozdev, 2010].
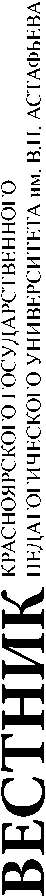
Результаты выполнения контрольной работы по темам «Сумма и разность многочленов. Произведение одночлена на многочлен» (процентное соотношение правильного выполнения заданий учащимися)
■ 7 «б» класс
7 «з» класс
Рис. 1. Результаты выполнения контрольной работы в экспериментальных классах
Fig. 1. Test results in experimental classes
Незначительное различие в процентах в выполнении заданий экспериментального и контрольного классов по заданиям 1 и 5 объясняется тем, что при изучении тем «Сумма и разность многочленов. Произведение одночлена на многочлен» учащиеся экспериментального класса только еще осваивали приемы применения компьютерной среды GeoGebra в учебном процессе. Процентное соотношение в других заданиях объясняется частичным использованием динамической среды на уроках алгебры.
Поскольку результаты контрольных срезов, представленные на рис. 1, все-таки носят до некоторой степени субъективный характер, то в порядке подтверждения было проведено дополнительное тестирование.
Тестирование охватывало те направления исследования, в которых реализация концепции компьютерной поддержки обучения алгебре предположительно должна была дать наибольший эффект.
Всего было выделено три таких направления:
-
1) умение выполнять сложение и вычитание многочленов;
-
2) умение выполнять умножение многочленов, умножение одночлена на многочлен;
-
3) умение выполнять разложение многочленов на множители.
Эти направления включены в тест, содержащий 12 заданий (первая часть - 10 заданий средней сложности, вторая часть - 2 задания повышенной сложности). Тест выполняли экспериментальные и контрольные классы. Тестовые задания составлены автором, и максимальное число возможных баллов по первой части – 10 баллов, по второй части – 5 баллов. При подборе тестовых заданий выполнялось требование – не допустить повышенных эффектов и обеспечить близость распределения испытуемых по количеству набранных баллов к нормальному распределению.
Сопоставление классов производилось путем сравнения средних баллов, набранных испытуемыми: л, - это средний балл по экспериментальному классу, – это средний балл по контрольному классу.
В качестве нулевой гипотезы H 0 принималось предположение о равенстве рассматриваемых средних баллов, т.е. H 0: \л = л., а другая гипотеза H 1 : \л * х. . Близость распределений испытуемых по набранным баллам к нормальному распределению и независимость выборок позволили в качестве статистического критерия применить t-распределение Стьюдента:
Хэ— хк г Ч
, где ,
-
3 к J n,+nft-2 X
где и – количество элементов выборок из экспериментального и контрольного классов соответственно, и – дисперсии распре- деления.
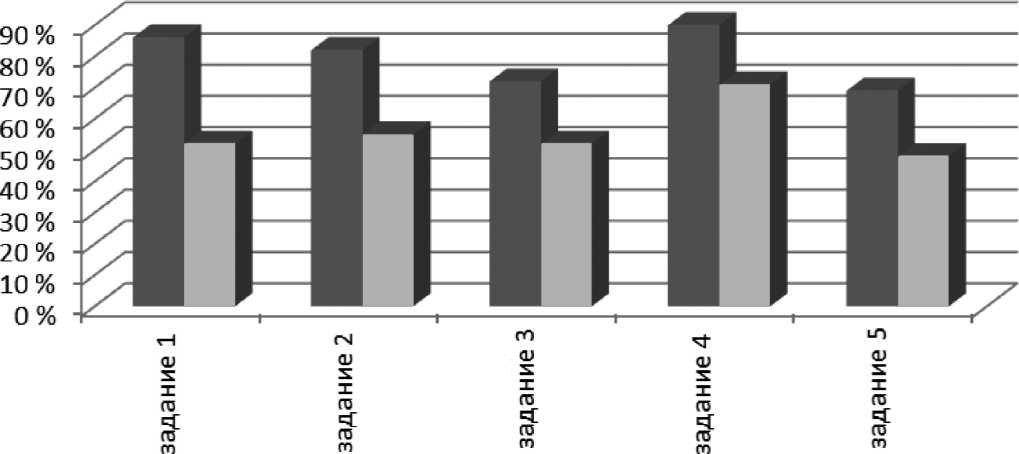
Для того чтобы избежать необходимости проверки на однородность дисперсий, брали выборки одинакового объема О- = "... = ;. ). Тогда:
— ■ — — ■ — ^~ । I—— ~I- “— I ~~
^з”^к J и+п-2 Хи и/ kn-l)-(S=+S=) ,2
■^ 2п—2 Si
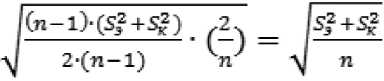
Проверка проводилась на уровне значимости с числом степеней свободы i = л? — ":. — 2. Таким образом, отсюда следует, i — 2?; — 2. Основные параметры результатов тестирования приведены в таблице.
Статистические характеристики результатов тестирования Statistical characteristics of test results
|
№ |
Направления исследования |
n – объем выборки (сроки проведения теста) |
средние |
средние |
s^ дисперсия |
дисперсия |
S—_— xs хх станд. отклон. по разн. |
^выч вычисленное |
^хрит критическое |
|
1 |
Умение выполнять сложение и вычитание многочленов |
50 |
3,8 |
3,5 |
0,58 |
0,35 |
0,19 |
1,58 |
1,985 |
|
2 |
Умение выполнять умножение одночлена на многочлен и многочленов |
50 |
3,3 |
2,8 |
0,29 |
0,8 |
0,21 |
2,38 |
1,985 |
|
3 |
Разложение многочленов на множители |
50 |
3 |
2,2 |
0,83 |
0,66 |
0,24 |
3,33 |
1,985 |
Число степеней свободы при n = 50 2. Направление, проверяющее выполнение равно 98, в этом случае при :7 = 0,0э, умножения одночлена на многочлен, умноже-tкрит =1,985. ния многочленов.
-
1. Направление, проверяющее выполнение 3. Направление, проверяющее разложение сложения и вычитания многочленов. многочленов на множители.
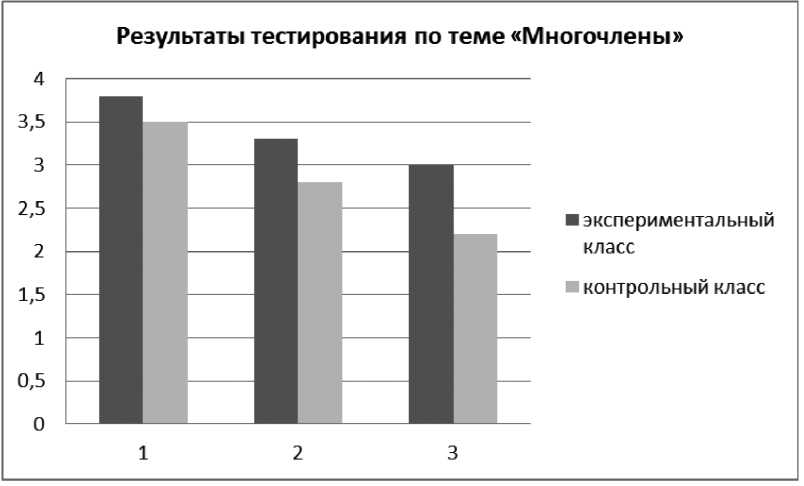
Рис. 2. Результаты тестирования по теме «Многочлены»
Fig. 2. Test results on the topic “Polynomials”
На рис. 2 приведены результаты тестирования. Из приведенной таблицы и рис. 2 видно, что наиболее существенная разница в результатах наблюдается в тех направлениях тестирования, где проверяются умения учащихся выполнять умножение одночлена на многочлен и умножение многочленов, а также умения выполнять разложение многочленов на множители.
Сравнивая параметры результатов в последних двух столбцах таблицы, видим, что из трех направлений два последние направления имеют tвыч > tкрит, откуда следует, что нулевую гипотезу в этих случаях следует отвергнуть, и, таким образом, превышение средних баллов экспериментального класса над соответствующими средними баллами контрольного класса статис- тически значимое. Только в первом направлении тестирования, где проверялось умение выполнять сложение и вычитание, превышение оказалось статистически незначимым.
Заключение . Систематическое использование компьютерных технологий в обучении математике активизировало участие учащихся экспериментальных классов в научно-исследовательской деятельности. Заинтересованность учащихся стимулировала нас на создание учебно-методического пособия «Уроки алгебры в 7 классе с анимационными рисунками».
Характерным показателем эффективности предлагаемой методики является то, что учащиеся экспериментальных классов ориентированы на использование компьютерной среды GeoGebra при изучении алгебры.
Список литературы Компьютерная анимация на уроках алгебры в 7-х классах: результаты экспериментальной работы
- Абдулкин В.В., Калачева С.И., Кейв М.А., Ларин С.В., Майер В.Р. Компьютерная анимация в обучении математике в педагогическом вузе: монография / Краснояр. гос. пед. ун-т им. В.П. Астафьева. Красноярск, 2019. 164 с. URL: http:// elib.kspu.ru/document/33659 (дата обращения: 10.10.2021).
- Бидайбеков Е.Ы., Ларин С.В., Бостанов Б.Г. Анимациялы математика: Оку куралы - Апматы: Абай атындагы Казак улпедагогикалык университету «Улагат» баспасы, 2019. 380 б.
- Дьяконов В.П. Математическая система Maple V R3/R4/R5. M.: Солон. 1998. 400 с.
- Зимнякова Т.С., Ларин С.В., Ларина Е.И. Особенности использования цифровых образовательных ресурсов в обучении математике и физике // Вестник КГПУ им. В.П. Астафьева. 2019. № 2 (48). С. 26-32. DOI: https://doi.org/10.25146/1995-0861-2019-47-1-117
- Ларин С.В., Чилбак-оол С.В. Использование компьютерной анимации в школьной алгебре чисел и многочленов // Информатизация образования и методика электронного обучения: матер. II Междунар. конф. Красноярск, 25-28 сентября 2018 г. Красноярск: СФУ. Ч. 2. С. 144-148.
- Ларин С.В. Компьютерная анимация в среде GeoGebra на уроках математики. Ростов-на-Дону: Легион, 2015. 192 с.
- Ларин С.В. Методика обучения математике: компьютерная анимация в среде GeoGebra. М.: Юрайт, 2018. 233 с.
- Ларин С.В., Казакова Е.В., Сивухина Е.А., Чилбак-оол С.В., Бурнакова М.В. О создании мультимедийного дидактического материала по алгебре 7 класса // Актуальные проблемы обучения математике в школе и вузе: межвуз. сб. науч. тр. Вып. 26. Посвящается 145-летию МПГУ. М.: ФБОУ ВО МПГУ, изд-во «Политоп», 2017. С. 99-103.
- Ларин С.В., Майер В.Р., Кочеткова Т.О., Карнаухова О.А. Особенности создания и использования компьютерных анимационных рисунков в обучении математике // Вестник КГПУ им. В.П. Астафьева. 2020. № 1 (51). С. 6-14. DOI: https:/doi.org/10.25146/1995-51-1-178
- Ломаско П.С., Симонова А.Л. Цифровизация образования - следующий этап информатизации или точка бифуркации? // Информатизация образования и методика электронного обучения: матер. II Междунар. конф. Красноярск, 25-28 сентября 2018 г. Красноярск: СФУ, 2018. Ч. 2. С. 149-153.
- Чилбак-оол С.В. Правый и левый алгоритмы Евклида для многочленов // Современная математика и математическое образование в контексте развития края: проблемы и перспективы: матер. III Всерос. науч.-практ. конф. студентов, аспирантов и школьников. Красноярск, 18 мая 2018 г. Красноярск, 2018. С. 91-96.
- GeoGebra: официальный сайт. URL: http://www.geogebra.org (дата обращения: 10.10.2021).
- Garner S. The CAS classroom // Australian Senior Mathematics Journal. 2004. Vol. 18, No. 2. P. 28-42.
- Grozdev S. Mathematics for economists. Sofia: VUZF, 2010 [Гроздев С. Математика за икономисти. София: Изд-во на ВУЗФ, 2010].
- Kramarski B., Hirsch C. Using computer algebra systems in mathematical classrooms // Journal of Computer Assisted Learning. 2003. Vol. 19. P. 35-45. DOI: 10.1046/j.0266-4909.2003.00004.x
- Larin S., Mayer V. The role of computer animation in mathematics teaching Mathematics and Informatics // Bulgarian Journal of Educational Research and Practice. 2018. Vol. 61, No. 6. P. 542-552.
- Sehovic E. The University and New Information Technologies // Higher Education in Europe. 1985. Vol. 10, No. 4. P. 13-10.
- Thomas M.O.J. Teachers using computers in the mathematics classroom; A longitudinal study // New Zealand Mathematics Magazine. 2006. Vol. 43, No. 3. P. 6-16.


