Компьютерная диагностика и управление процессом обучения

В настоящей работе анализируется другая ситуация, когда в компьютерной системе управления процессом научения есть модуль, который играет роль исполнительного органа. В этом случае в основе управления деятельностью ученика лежит механизм компенсации неправильных действий обучаемого. Например, компьютер исправляет неправильные операции, совершаемые учеником, или устанавливает запрет на некоторые операции, совершаемые учеником через клавиатуру или мышку, и т.п. В этом случае компьютерная система компенсирует неопределенность объекта. Надо отметить, что исполнительные органы ученика действуют и в этом случае. Более того, компенсационные управляющие воздействия, которые произведены компьютером, воспринимаются учеником как сигналы управления, которые подвергаются перекодировке в управляющем устройстве ученика (в мозгу).

Таким образом, ученик рассматривается как неопределенный объект управления. Поведение ученика характеризуется рядом параметров, совокупность которых можно обозначить вектором 0 . Вектор 9 может включать в себя неизвестные параметры объекта, неточно известные характеристики, неизмеряемые внешние возмущения и т.д.

Структурная схема компенсаторной системы управления, в которой реализуется оптимальный (в определенном смысле) процесс управления, представлена на рис.1.

Положим, что локальная цель управления состоит в том, чтобы обеспечить наименьшее значение некоторой величины (функционала) R 1 , зависящей в общем случае от функций задающего x в (t) и управляющего u(t), воздействий и от управляемой величины x(t), т. е.

R i [ x в (t ), x (t ), u (t )] = R _min . (1)

Главная цель определяется целевым неравенством:

R ₂( x, t ) <А . (2)

Эти цели должны быть достигнуты при наличии определенных ограничений, состоящих в том, что некоторые величины (функционалы) F i , где i = 1, 2,..., m , не должны превосходить установленных для них значений, т. е.

F [ x в (t ), x(t ), u(t ), z(t )] <  F i ,

где z(t) - возмущение, воздействующее на объект управления.

Роль функционалов F i могут играть ограничения на время T или число заданий N, отводимых на обучение студента. Управляемой величиной R i (формула (1)) является расстояние между текущим и целевым состоянием задачи в проблемном пространстве задачи. Целевое неравенство (2) определяется для функции ценности состояния R 2 [3] .

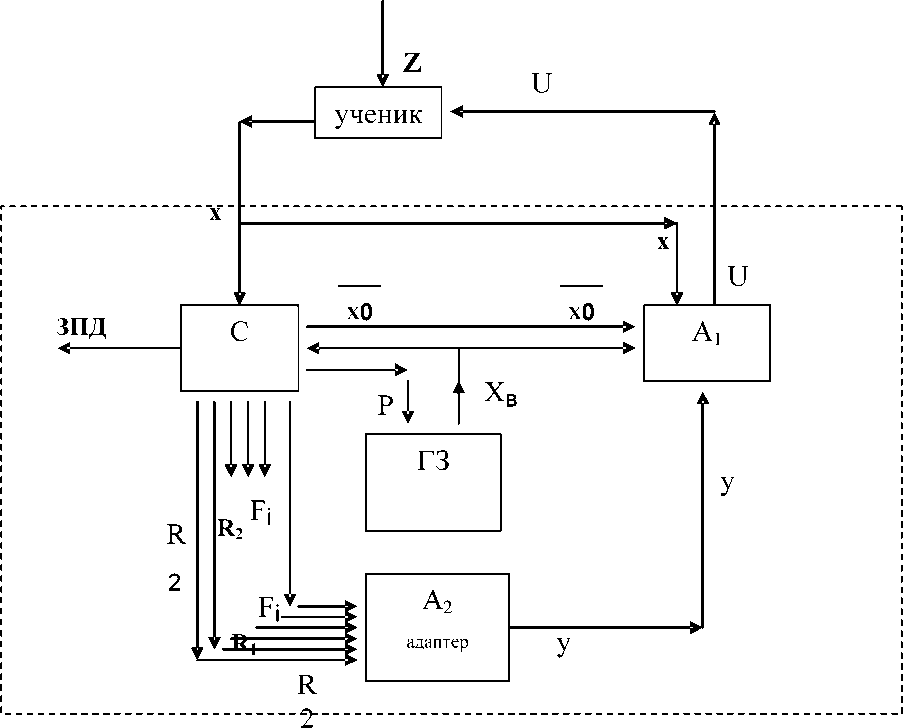
Рис .1. Структура управления обучающей и диагностирующей компьютерной системы с компенсационным механизмом :

ГЗ — генератор заданий ; A i — интерфейс ученика ; A 2 — управляющий модуль ( адаптер ); С — вычислительный модуль ; ЗПД — запись продуктов деятельности ученика ; X в — за дающее воздействие ( задание ); U — управляющее воздействие ; Z — возмущение ; x — управ ляемая величина ( действия ученика ); х0 — компенсатор ; P — управление ГЗ; R i и R 2 — кри терии оптимальности ; F i — функционалы ; у — корректирующее воздействие

Как уже говорилось выше, полная априорная информация относительно z(t) и x(t) отсутствует. В рассматриваемой системе управляющее устройство A 1 представляет собой интерфейс студента, являющийся преобразователем входов x, X в x0, y и выхода U . А 2 может воздействовать на A 1 , перестраивая его алгоритм. Основываясь на главной и локальных целях управления, устройство А 2 с помощью алгоритмов обучения и по мере накопления опыта, который определяется совокупностью реакций A 1 на возможные изменения режимов работы студента, вырабатывает воздействия y(t) и x0 , которые все более и более приближаются к требуемым значениям. Требуемыми являются такие значения y(t) , x0 , которые в соответствии с получаемыми в вычислительном устройстве С значениями критериев оптимальности R 1 и R 2 (при ограничениях F* i ) перестраивают алгоритм работы A 1 таким образом, что выполняются условия (1) – (2). На вход вычислительного модуля С поступает информация о действиях студента x и о заданиях, которые генерируются модулем ГЗ . Вычислительный модуль С осуществляет слежение за деятельностью ученика при выполнении задания в режиме on-line. При этом на основании сравнения с критерием оптимальности R 1 вычисляется функция вознаграждения [1; 3]. Это позволяет определить значение функции ценности состояния и выработать в модуле A 2 корректирующее воздействие y(t), помогающее студенту достичь главной цели (2). Величину функции ценности состояния ученика y(t) м одуль A 2 изменяет в соответствии с относительной частотой правильных действий p , вычисляемой после каждого задания. Информация об окончании выполнения задания, так же, как и информация об окончании работы с системой, передается в модуль ГЗ по каналу P. Наряду с перечисленными функциями вычислительный модуль С производит не только слежение за действиями ученика, но и записывает информацию о деятельности, которая представляет собой протокол, включающий: 1) действие; 2) время; 3) «штраф» (–1) или «вознаграждение» (+1); 4) величину функции ценности состояния ученика R 2 . Продукты деятельности ученика записываются в текстовой файл (выход ЗПД ) для последующей диагностики динамических характеристик процесса научения.

Рассмотрим математическую обработку продуктов деятельности, полученных в результате динамического тестирования студентов факультета физики, информатики и ВТ [4]. Динамическое тестирование проводилось по теме «Кривые второго порядка». Студенты должны были обучиться конструированию кривых второго порядка по заданным уравнениям.

В процессе научения решению задач обучаемый, решая серию аналогичных задач, совершает различные действия ( A j ). В нашем случае эти действия связаны с операциями параллельного переноса, растяжения, сжатия и поворота. При этом множеству альтернатив A j , соответствует множество вероятностных переменных P j. Однако наибольший интерес представляют две альтернативы: A 1 («правильные действия») и A 2 («неправильные действия»), вероятности появления которых равны соответственно P и 1 – P .

Основные приближения математической модели состоят в том, что вероятность P в процессе выполнения i-го задания полагается постоянной и стохас- тическая модель обучаемости линейная [2]. Последовательность событий Ei состоит из выполненных заданий, i – номер задания.

Отдельное событие E i представляется строчным математическим оператором Q i , который записывается в виде:

Q i P = a P + ( 1 - а ) Я ,                                (4)

где α и λ – параметры, которые характеризуют обучаемого ( λ – предельное значение вероятности Р). Величина α принимает значения от –1 до 1 и показывает скорость выхода на уровень неподвижной точки (величина λ ), который принимает значения от 0 до 1.

Если до наступления события E i вероятность события A 1 есть Р , то Q i P есть вероятность этой реакции после наступления события E i . Следовательно, если событие E i наступает еще раз, то необходимо применить оператор Q i к вероятности Q i P . Полагая, что событие E i наступает n раз, получаем общую формулу для случая n применений оператора:

Q - P = a - p + ( 1 - a n U .                          (5)

Параметры α и λ определяются методом «наименьшего квадратичного отклонения». Данное рекуррентное соотношение дает дискретное описание экспериментального временного ряда событий (рис. 2, графики 1, 2). Непрерывная аппроксимация решения рекуррентного уравнения (5) имеет вид:

• У = e -t^ i ) n p + (1 - e -t^ i ) n )Л_;,                             (6)

где y – вероятность правильного действия на n+1 задании, λ и α имеют тот же смысл, что и при рекуррентном соотношении.

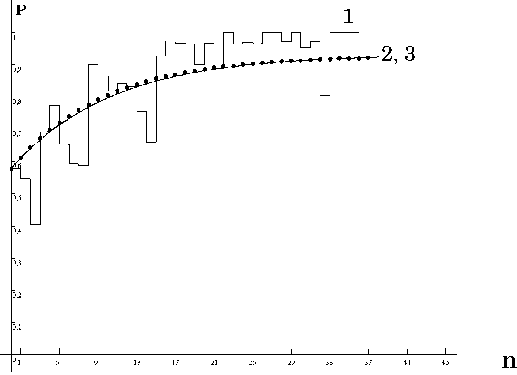
Рис 2. Вероятность правильных действий в зависимости от числа заданий для испытуемого под номером 12:

• 1    – экспериментальная зависимость вероятности правильных действий от числа заданий ;

• 2    – рекуррентная зависимость изображена точками ( α =0,91, λ =0,931);

3 – график функции (3), ( α =0,95, λ =0,935)

Выражение (6) является разумной аппроксимацией, если величина 1-α мала по сравнению с единицей [2]. На рис. 2 аппроксимация экспериментальных данных с помощью формулы (6) представлена графиком под номером 3.

Динамическое тестирование процесса научения решению задач было произведено на выборке из 85 студентов факультета физики КГПУ. В результате получена гистограмма плотности распределения испытуемых по параметру λ (рис. 3). Видно, что распределение имеет асимметричный характер с выраженным максимумом f = 7,53 при λ = 0,92. Среднее значение параметра λ = 0,745 при ∆ λ = 0,03125, а дисперсия D = 0,025.

Из гистограммы плотности распределения видно, что небольшая группа студентов имеет предельное значение вероятности правильных действий 0,5 – 0,6. Студенты этой группы, несмотря на достаточно большое количество выполненных заданий (свыше 30), не достигли «индуктивного порога» [3]. Их деятельность осталась на уровне метода проб и ошибок.

Полученные результаты подтвердили целесообразность использования линейного приближения для анализа экспериментальных временных рядов событий E i , полученных при динамическом тестировании. Однако линейное приближение налагает жесткие ограничения на значения параметра α (см. выше).

Гистограмма плотности распределения (f) испытуемых по параметру лямбда ( λ )

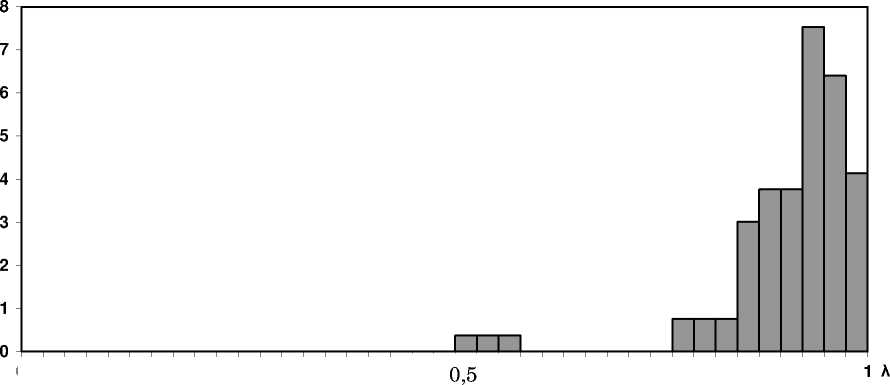
Рис 3. Гистограмма плотности распределения обучаемых по параметру λ

Нелинейное описание снимает эти ограничения, однако в настоящее время оно отсутствует.