Концентрическая модель построения учебного курса, ориентированного на реализацию внутрипредметных связей

учащиеся при изучении того или иного предмета получают лишь базу данных: изучаемый учебный курс предстает перед школьником в качестве базы знаний только при условии установления в нем логико-содержательных и структурно-функциональных связей [3].

Исследования внутрипредметных связей до сих пор находятся в тени обширного поля межпредметных связей. Причиной этого может быть мнение, что интегрировать, связывать необходимо лишь знания, относящиеся к разным предметным областям и, соответственно, к разным учебным дисциплинам. Однако поскольку каждый учебный предмет оперирует своим набором понятий, законов, принципов, правил (структурных элементов учебного курса), то реализация связи данных элементов, как обычно определяют внутрипредмет-ные связи отечественные исследователи [2], представляется одним из наиболее важных системообразующих факторов процесса обучения. В зарубежной педагогике внутрипред-метные связи (intradisciplinarity) вводятся как подкласс межпредметных связей, объединяющих такие близкие учебные предметы, как, например, алгебра и геометрия или чтение, письмо и речь [4].

Следует отметить, что основная часть исследований, выполненных в области внутри-предметных связей, посвящена внутрипред-метным связям курсов физики и математики. Это обусловлено тем, что основой построения системы внутрипредметных связей является понятийный аппарат изучаемой дисциплины. И именно курсы физики и математики предлагают к освоению широчайший спектр понятий, систематизировать который и можно посредством реализации связей. В данной статье мы остановимся на концентрическом варианте построения учебного курса, который позволяет активно реализовать внутрипредмет-ные связи.

Обычно учебный курс, рассчитанный на один-два года, имеет линейную структуру в изложении материала, т.е. каждая тема изучается только один раз без возвращения к ней на более сложном или качественно ином уровне. Трехлетние и более длительные курсы могут иметь концентрическую структуру. При этом, как правило, расположение материала по виткам или ступеням примерно схожее.

В качестве примера подобного курса можно привести школьный курс физики. Здесь содержание разделено на два цикла, причем второй цикл, наследуя от предшествующего систему понятий, законов и методов, существен- но усложняет формируемую физическую картину мира, используя и существенно усложненные модели, и расширенный математический аппарат.

Близкую по смыслу, но иную по варианту реализации концентричность имеет курс математики (объединения алгебры и геометрии). Здесь сначала вводится и рассматривается на простейших примерах понятийный аппарат, а затем в 10–11-х классах на основе полученных знаний происходит расширение свойств понятий. Ярким примером могут служить периодические обращения к понятию функции на разных этапах курса алгебры или изучение тригонометрических функций, изначально вводимых в курсе планиметрии с существенным углублением уже в курсе алгебры 10-го класса.

Уже такое «крупномасштабное» концентрическое построение учебных курсов позволяет активизировать процесс реализации вну-трипредметных связей, т.к. систематическое обращение к изученным понятиям и законам, вплетенное в канву нового материала, в той или иной степени стимулирует образование связей.

Концентрическую структуру могут иметь не только многолетние, но и годичные учебные курсы, элективные курсы объемом от полугода до двух лет, и даже изучение отдельных разделов дисциплины может быть построено концентрически. Для этого мы предлагаем строить концентры не только за счет усложнения материала, а путем поэтапного перехода от рассмотрения реальных объектов и явлений к абстрактным моделям и решению задач.

При концентрическом построении первый цикл курса должен содержать максимально широкий и полный обзор реальных объектов и явлений, послуживших базой для научного исследования методами изучаемой дисциплины. Данный цикл преследует несколько целей. Во-первых, школьники актуализируют свой бытовой опыт и соотносят его с изучаемым материалом. Это дает учащимся ответ на уже ставший традиционным вопрос: «Зачем мы все это учим?». Во-вторых, здесь на реальных объектах можно ввести основные понятия, привязав их к зрительным образам, а если в демонстрациях используются материальные модели, то и к тактильным ощущениям. Другими словами, в процессе формирования основных понятий школьники задействуют несколько каналов восприятия, что позволит значительно глубже закладывать фундамент внутрипред-метных связей. В-третьих, целью, созвучной с первой, является необходимость компенсации недостатков в практических знаниях и навыках школьников, что прямо отражается на понимании. Данная проблема сейчас стоит особенно актуально, поскольку общество постепенно приобретает статус информационного, что зачастую экранирует учащихся от материального мира и дезориентирует их при обсуждении даже достаточно простых практических вопросов.

В первом цикле можно выделить еще один «мини-цикл». Желательно познакомить школьников с историческими корнями исследований в изучаемой области знаний. Данный шаг может служить еще одним аргументом в пользу необходимости изучения предлагаемого в курсе материала, поскольку в качестве довода мы приводим не только желание учителя дать знания своим подопечным, но и вполне реальные задачи, которые решались классиками науки вплоть до времен древней Греции, Египта или Китая. Подобные примеры обычно привлекают внимание школьников к изучаемому материалу.

Второй цикл предполагает построение и изучение свойств графических моделей рассмотренных в предшествующем цикле объектов и явлений. Данный шаг необходим для того, чтобы максимально плавно перейти от реальных объектов к их моделям, которые впоследствии и будут изучаться школьниками. Графические модели, с одной стороны, наиболее близки к материальным, соответственно, они легче воспринимаются и интерпретируются на основе полученных школьниками знаний, с другой – готовят учеников к необходимости более точного, математического описания явлений. Кроме того, графические модели позволяют как уточнить определения основных понятий, так и прояснить их взаимосвязь, т.е. сделать еще один виток в реализации внутрипредметных связей.

Графические модели могут быть произвольные: построенные на бумаге или отображенные на экране, плоские или трехмерные, статические или динамические. Здесь важно лишь помнить, что модель призвана наилучшим образом отображать характерные черты моделируемого объекта.

Третьим должен быть цикл построения и исследования свойств математических моделей изучаемых явлений и объектов. На данном этапе исходные явления, как и их графические модели, должны получить точное математическое описание, математическую формулировку, математическую модель. Поскольку мы говорим о конструировании относительно крат- косрочного учебного курса, то обычно к рассмотрению принимаются явления, сходные по типу и зачастую имеющие либо единую, либо близкие математические модели. Это позволяет обобщить понятия и придать внутрипред-метным связям как качественный, так и количественный характер.

В этом цикле также необходимо продемонстрировать универсальность математических моделей, их пригодность к описанию объектов и явлений самой разнообразной природы. Ярким примером подобного объединения относительно простых моделей является работа В.И. Арнольда [1], в которой автор одной моделью смог описать, например, элементы движения Марса по орбите, реактивную тягу самолета и «путь пьяницы домой». Формально являясь математическими, рассматриваемые модели по своей сути должны отражать специфику учебного предмета, т.е. математические модели курса физики должны передавать математическую сторону физических закономерностей (уравнения движения, законы сохранения и т.д.). Именно закономерности, соотношения между величинами, количественными характеристиками понятий позволяют реализовать внутри-предметные связи.

Четвертый цикл концентрической модели построения учебного курса предполагает знакомство с максимально широким спектром задач, которые могут быть решены в рамках изученных моделей. Данный цикл сам по себе может иметь концентрическую структуру, поскольку при большом количестве задач можно возвращаться к одному материалу несколько раз на разных уровнях сложности и при использовании различных методов и подходов к решению задач.

В процессе реализации внутрипредметных связей решение задач играет наиболее важную роль. Дело в том, что возможности подбора задач как по тематике, так и по уровню сложности практически не ограничены. Соответственно, с их помощью можно задействовать в учебном процессе наиболее существенные связи, подстраивая, адаптируя учебный процесс в конечном счете под каждого ученика, что позволяет говорить о возможностях дифференцированного подхода к учебному процессу и о возможностях выделения на этом этапе индивидуальных траекторий обучения. Поскольку решение задач позволяет реализовать максимально различные варианты связей, можно говорить о построении сетевой структуры внутрипредметных связей за счет актуа-

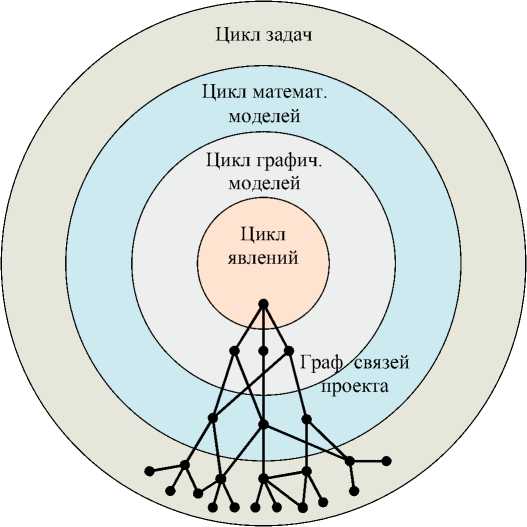
Графическое представление концентрической модели учебного курса и графа связей учебного проекта

лизации не только прямых, но и опосредованных связей.

Последний, пятый, цикл является надстройкой над предыдущими. Его можно не выделять специально отводимыми учебными часами, хотя при избытке последних это желательно сделать. Данный цикл должен быть посвящен выполнению учебного или учебноисследовательского проекта.

Выполняемый школьниками учебный проект замечателен, прежде всего, тем, что при его выполнении появляется возможность интегрировать системы внутрипредметных и межпредметных связей, создавая тем самым сложную, многоуровневую систему связей. Оптимально, если проект будет ориентироваться на глубокое изучение явления, рассмотренного в первом цикле, и использование моделей, методов второго и третьего циклов. К тому же выполнению проекта могут способствовать корректно подобранные в четвертом цикле задачи.

Реализация одного проекта не может покрыть всю систему рассмотренных в учебном курсе внутрипредметных связей. Тем не менее проект способен покрыть определенную область системы связей (см. рис.).

Описанная выше модель обладает свойствами гибкости и делимости. Прежде все- го, наполнение модели содержанием в соответствии с основной темой курса может отличаться высокой степенью вариативности, поскольку от составителя зависит, какой материал он возьмет за основу, какие модели будет использовать, какие задачи предложит школьникам.

Следует отметить, что модель позволяет построить учебный курс в соответствии с движением от рассмотрения реальных объектов и явлений путем абстрагирования к математическим моделям и задачам. В связи с этим модель можно адаптировать для разных уровней обучения. Например, для гуманитарного профиля в модели можно оставить первые два-три цикла, существенно сократив или упростив четвертый. Если же готовится элективный курс для профильного физико-математического класса продолжительностью в один год, то наполнение модели материалом должно быть максимальным вплоть до разработки перечня тем учебноисследовательских проектов.

При использовании концентрической модели построения учебного курса, ориентированной на реализацию внутрипредмет-ных связей, возникают определенные трудности, которые можно прогнозировать заранее. В частности, методисту, определивше- муся с компонентами реализуемых в курсе внутрипредметных связей, удобнее будет наполнять курс содержанием с цикла математических моделей, поскольку они являются узловыми точками системы связей. Под уже выбранную систему моделей проще подобрать и задачи, и описываемые этими математическими моделями явления и объекты.

Может составлять определенную сложность и подбор системы задач, максимально полно реализующей внутрипредметные связи. В то же время именно цикл задач может быть построен максимально гибко, отражая специфику предмета и адаптируясь под особенности аудитории.

Подводя итог сказанному выше, отметим, что концентрическая модель позволяет оптимизировать структуру учебного курса под процесс реализации внутрипредметных связей, но не менее важно, чтобы был подобран соответствующий учебный материал под этот процесс и использована методика, адекватно отражающая реализуемую систему связей.