Конечно-элементный анализ задач теории упругости с заданными скачками искомых функций в пакете ANSYS при использовании суперэлементного подхода

В работе рассматривается использование программы ANSYS для решения задач теории упругости с заданными скачками искомых функций. Подобные задачи возникли в теории сейсмостойкости массивных сооружений, где такие постановки были получены путем математически строгих преобразований [1–3].

Особенностью рассматриваемых задач является наличие внутренних контактных границ (линий, поверхностей), содержащих в условиях контакта заранее известные разрывы (скачки первого рода) искомых функций перемещений и усилий. Обсуждение реализации в ANSYS заданных скачков ограничено в настоящей работе рассмотрением статической постановки задачи, поскольку цель работы – показать принципиальную возможность внедрения подобных алгоритмов в пакет ANSYS. Заметим, что такое расширение данной программы представляется весьма привлекательной формой ее использования для исследовательских целей, т.к. при этом открывается возможность изучать новые модели, используя привычный функциональный интерфейс и мощные решатели пакета.

1.    Постановка задачи

Рассмотрим статическую задачу теории упругости с заданными скачками искомых функций. Пусть исследуемая область V разделена достаточно гладкой поверхностью ю так, что V = V + V и д V = S , д V ₂ = S ₂, S И S₂ = ю . Запишем дифференциальную постановку рассматриваемой задачи [3, 4] в матрично-векторных обозначениях:

• (A) T^a + Y = 0 ^еV,

  £' = Аи,	еV,
  ст = Ds i     ii	еV,
  ( AS, ) T &   gs,	е Su,   (i = 1,2)      (1)
  ui = us,	е S2 i ,
  [ и ] = U	е ю,
  -[(Аю ) T&] = P	е ю.

2.    Конечно-элементная реализация

Квадратными скобками здесь обозначен скачок стоящей в скобках величины при переходе через границу контакта областей, например: t( ^А _ш ) T & ^] = ( ^А _ш ) T & - ( A ) T & 2 ; матрица направляющих косинусов А_ш берется с плюсом для области V . Описание остальных используемых обозначений можно найти в работе [5].

Вариационные постановки для исследуемых задач отличаются от обычных наличием интегралов по границе контакта областей ю [3, 4]. Например, если обозначить через П ( и ) сумму функционалов Лагранжа для областей V и V₂ в задаче без скачков перемещений и усилий, а через П_с ( и ) - функционал Лагранжа в задаче со скачками, то

п ( и ) = П ( и ) - 2 j ( k и + k₂ u ₂) T P d a . (2) ω

В функционал (2) могут входить различные численные величины k , k , удовлетворяющие условию k + k₂ = 1. Очевидно, что отвечающие этим функционалам уравнения Эйлера, равно как и решения самих задач со скачками, от k и k₂ зависеть не будут. Функционал (2) определен на классе функций, удовлетворяющих кинематическим краевым условиям на S_2;. и заданным кинематическим условиям контакта на границе контакта областей ю .

Конечно-элементная дискретизация выполняется обычным образом, за исключением некоторых специальных требований в связи с наличием поверхности ω . Чтобы иметь возможность реализовать негладкие условия контакта, узлы конечно-элементной сетки, принадлежащие границе ω , нумеруются дважды таким образом, чтобы один номер относился к области V , а другой - к V .

После обычной процедуры конечноэлементной дискретизации получим систему линейных алгебраических уравнений:

KU = F + F , (3)

где U - искомый вектор узловых перемещений, K - матрица жесткости, F - обычный вектор усилий, в который в соответствии с функционалом (2) входят узловые значения векторов объемных и поверхностных усилий, F - вектор узловых значений, отвечающий заданному значению скачка усилий на поверхности ω . Таким образом, учет значения скачка в усилиях реализуется аналогично обычным краевым условиям в усилиях. Однако общая конечно-элементная реализация скачка в усилиях включает еще преобразование матрицы жесткости и означает реализацию условия контакта в перемещениях на границе ю (со скачками или без скачков). В работе такое преобразование выполняется с помощью реализованного в пакете ANSYS суперэлементного подхода и обсуждается ниже.

К системе (3) следует добавить два уравнения, обусловленных кинематическими граничными условиями - заданными перемещениями на границах S и заданным скачком вектора перемещений на границе ю :

U, = и е S ₂,, ( i = 1,2) i S i 2 i

^{[ U ]} = u a ^{е Ю} .

Техника реализации скачка в перемещениях хотя и похожа на реализацию кинематических граничных условий, так как в некоторой степени означает исключение соответствующих неизвестных из результирующей СЛАУ, однако может быть выполнена по-разному. В работе предложен способ, сохраняющий размерность и симметричность матрицы СЛАУ.

3.    Решение модельной задачи в пакете ANSYS

Для реализации заданных скачков было рассмотрено несколько способов программного взаимодействия с пакетом ANSYS, и был выбран суперэлементный подход. Суперэлемент в пакете ANSYS определяется как группа конечных элементов, которые рассматриваются как один элемент с выбранными главными степенями свободы, причем он полностью определяется своим бинарным файлом, в ко- тором хранится вся необходимая информация, включая матрицу жесткости и вектор узловых нагрузок [6]. Поскольку ANSYS предоставляет функции для программного создания, чтения и модификации бинарных файлов суперэлементов [7], взаимодействие с пакетом ANSYS через бинарные файлы суперэлементов было выбрано для необходимой модификации матрицы жесткости.

В качестве модельной задачи рассмотрена задача определения напряженно-деформированного состояния плоской упругой области, протяженной в горизонтальном направлении и содержащей границу а, которая делит ее на две части (левая часть – V , а правая – V ), возможно, имеющие разные механические характеристики (рис. 1). На границе контакта областей а были заданы скач- ки в усилиях и перемещениях.

Однородные краевые условия на границе расчетной области и скачок задаются таким образом, чтобы в задаче была симметрия относительно горизонтальной осевой линии. В этом случае решение модельной задачи от- носительно x -овых компонент решения с хорошей степенью точности может быть аппроксимировано решением соответствующей одномерной задачи:

U = c (x -12),  CTj = cE,  Cj u2 = c2x,     o2 = CE,  c2

UE₂ + Pl, E ₂( l i - 1 2 ) - E i I/ UE' + P (4 - 1 ₂) E 2 ( l i - 1 2 ) - E i l i ^.

Здесь u, , сг_; - перемещения и напряжения в области V ; E – модуль упругости в области V ( i = 1,2); U , P - заданные скачки перемещений и усилий на границе а ; 4 , l₂ -длина левой части области и протяженность всей области соответственно.

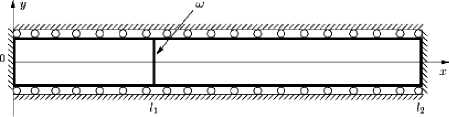
Рис. 1. Расчетная область с заданными скачками на границе контакта а

При моделировании расчетной области в пакете ANSYS выполнено условие двойной нумерации узлов, принадлежащих границе а .

В качестве суперэлемента выбраны два слоя конечных элементов, аппроксимирующих границу а , - один слой элементов принадлежит области V , а другой – V .

После стандартной процедуры создания суперэлемента и записи его бинарного файла последний модифицируется необходимым образом с помощью разработанной программы, которая считывает из бинарного файла матрицу жесткости и вектор нагрузок суперэлемента, преобразует их с учетом скачка в перемещениях и записывает обратно в файл. Модифицированный суперэлемент, в котором уже учтен скачок в перемещениях, используется для решения исходной задачи. После выполненного преобразования этап решения не отличается от решения стандартной задачи, содержащей суперэлемент как часть расчетной модели.

Расчеты производились при следующих данных: 4 = 4 м , l ₂ = 10 м ,

E = E ₂ = 1.09 - 10¹⁰ Па , U = 10 - ⁴ м , P = 10 5 Па .

Результаты решения в пакете ANSYS поставленной задачи хорошо согласуются с аналитическим решением (рис. 2).

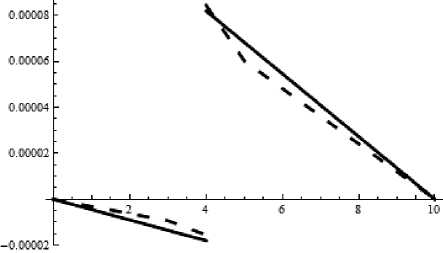
Рис. 2. Графики искомых функций перемещений (сплошной линией обозначено аналитическое решение, пунктирной – решение в пакете ANSYS)