Корректность обратной задачи акустики
Автор: Тюлепбердинова Г.А., Аханаева А.Д.
Журнал: Вестник Алматинского технологического университета @vestnik-atu
Рубрика: Естественные науки
Статья в выпуске: 6 (96), 2012 года.
Бесплатный доступ
В этой статье доказывается условная корректность обратной задачи акустики. В работе в вычислениях нормы всех компонентов были оценены через норму вектора q, поскольку оценка нормы вектора q является суммой оценок его компонент. И в данной статье, как это сказано, оценки каждого его компонента уже использовались непосредственно. В отличие от доказанной учеными подобной теоремы, в заключении потребованной константы в основном неравенстве используется не векторная оценка q, а оценка каждого его компонента.
Акустика, обратная задача, корректность, вектор, компонент, нелинейное уравнение
Короткий адрес: https://sciup.org/140204612
IDR: 140204612 | УДК: 517.538.7
Текст научной статьи Корректность обратной задачи акустики
Рассматривается динамическая обратная задача для уравнения акустики. Для применения градиентного метода Ландвебера, разрабатываются вычислительные методы решения нелинейной обратной задачи акустики. Доказываем условную устойчивость решения системы нелинейных уравнений Вольтерра
[1] и определям константы устойчивости (постоянные Липшица).
Определение 1 (Класс решений обратной задачи). Будем говорить, что ст ( x ) gL ( l , M ст , c 0 ,p 0 , ст *) , если ст ( x ) удовлетворяет следующим условиям:
ст ( x ) g H 1 (0, l ), HI H i (0, l ) < M c , 0 < ст * < ст(x ), x G (0, l ), ст 0 = c 0 P o .
Определение 1 (Класс исходных данных). Будем говорить, что g g G ( l , в, Y ) , если g удовлетворяет следующим условиям: g g H '(0,2 l ), || g -||2 < в , g ( + 0) = - Y ,
L 2 (0,2 l )
Объекты и методы исследований:
Предположим, что для для g(1) , g(2) из класса G(l, β,γ) существуют ст(1),ст(2) eS(l,Mct,c0,Po,ст*), удовлетворяющие обратной задаче
u(j) (x, t) = u(j)(x, t) - (CT )(x) u(j)(x, t), x > 0, t > 0,
tt xx σ(j) (x) x для j = 1 и j = 2.
Учитывая, что
5 (j) ( x ) = - у^ст ( j ) ( x )/ ст ( j ) ( + 0), обозначим
u ( j )( x , t )l t < 0 - 0 , (2) u ( j ) ( + 0, t ) = y5 ( t ), t > 0, (3) u(j )( + 0, t ) = g ( j )( t ), t > 0. (4)
( j)(xA-u(j)(xt\ j )Сх) 1 j )^х) -Q-^ ^-^x )
q. (x, t) u (x, t), q, (x) x, q 3( x) 2 .
1 x 2 s ( j ) ( x ) s ( j ) ( x )
‘»
f 1( j ) ( x , t ) = ( g ( j ) ) ( t + x ) -( g ( j ) ) ( t - x ), f ,( j ) =—, f 3j )( x ) = —^—2----, j = 1,2.
J уу
Поскольку
CT ( j ) G 2 ( l , M ct , c 0 , P 0 , CT * ), j = 1, 2, то в силу обозначений можно оценить
II
q
где M q = M q ( l , M ct , у , в , ст * ). Пусть вектор-функция q = ( q 1 , q 2, q 3) T , удовлетворяет системе:
q ( x , t ) + Bq ( x , t ) = f ( x , t ), ( x , t ) g A ( l ).
Решение задачи Aq = f предполагается, но утверждается, что существует единственное устойчивое решение для данных из окрестности точно заданных, то есть накладывается ограничение на шум во входных данных.
Для условной корректности рассматриваемой задачи, в отличие от аналогичной теоремы в [2] в нижеприведенной теореме при выводе требуемой константы в основном
неравенстве использовалась не оценка вектора q, а оценки каждой из его компонент q 1 , q 2 , q 3. В работе [2] в выкладках норма каждой компоненты оценивалась через норму вектора q, так как оценка нормы вектора q есть сумма оценок его компонент. А в данной статье, как сказано выше, уже использовались непосредственно оценки каждой из его компонент q 1 , q 2 , q 3.
ii2 2 lM2 о ii2 2 l f lM 2 1 II II2
II q j L 2(A( l )) < 2 1 exp I f в l q 21 L (0, l ) < -T exp I -^ к Il q з1 L 2(0, l )
- * Y l^ - * J
< ... - II » 1 (07, = 1? M- σ * σ *
Теорема Предположим, что для f mg L 2 ( l ), j = 1,2, существуют решения
обратной задачи q ( j ’ g L 2 ( l ), j = 1,2
q ( j ’ ( x , t ) + Bq ( j ’ = f ( j ’ ( x , t ), j = 1,2, ( x , t ) gA ( , ). (8)
Тогда
I q 1 - q 12 < C ilf1’ - f ' 2'| 12
II II L 2( , ) II II ! 2 ( ) )
Здесь
Ci =
15 +
v
50 M σ 2 γ 2 σ * 2
5 lM
+ —2 σ *
1+ v
5 M 2 ) ,2
/ — * у
exp ।
lM σ 2 2 σ * 2
AJ
x expIl 3l + 5в +
25 ) j M2
-- —- + 2 2
Y J - *
Г l 2 25 l2M2
+
V Y 2y - *
10 ,e) +J
expI
lM σ 2
2 σ * 2
+ 10 eiMf + 51в +
V - *
702 j
Y J
exp ।
2 lM ^ 1
- *2
+ 55 l 2 вМ^ γ 2 σ * 2
expI
5 lM σ 2 2 σ * 2
Доказательство. Введем
~( x , t ) = ( ~ 1 ( x , t ) ~ 2 ( x ) ~ з ( x ) ) = q (1) ( x , t ) - q <2) ( x , t ), f ( x , t ) = ( f ( x , t ) f , ( x ^f 3 ( x ) ) = f (1) ( x , t ) - f (2) ( x , t ),
‘(f) (x) = (f ">)(x)-(f)(x).
Тогда из (8) следует
~( x , t ) = Bq (1)( x , t ) - Bq <2)( x , t ) = f ( x , t ), ( x , t ) g A ( l ).
Оценим первую компоненту q ~1 :
I ~ 1 ( x , t )| = | f ( x , t )| + 2 1 |~з] ( x )
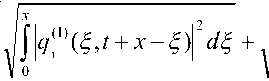
x
J q I1) ^ , t - x + 2 )|2 ^2
+ 21 q 32)ii( x )
xx
J f* 1) ^ ; , ! + x - 2 ) d2 + J f^C ^ , ! - x + 2) d2 00
Учитывая, что
n
z
V i = 1
^ 2 ai
n
< n Z a
V i = 1 7
для a i > 0 , получим
| ~ 1 ( x , t )| 2 < 5| / . ( x , t )| + 51 Ы|2( x ) x j q (1) ( 5 , t + x — 5 )1 2 + q (1) ( 5 , t — x + 5 )1 2 d^
x
+ 1 l q 32) l( x )f [~2 ( 5 , t + x — 5 ) + ~2 ( 5 , t —
Имеем x 2l-5
ξ
0 ξ
2 ξ
x||q32)|| (5)Д~2К',т + 5 — 5’) + ~2(5',t
x
—
5 + 5 ' ) ^5 ' * dTd5
, t — 5 + 5 ')| 2 d5
Оценим вторую компоненту:
xx
5 j| q (2)||2 ( 5 )|.~ , |'< i , 5 ) d5.
Следовательно,
II ~ 1 x ) < 2
x
| q 3"||2 ( 5 )||~ 2||2 ( 5 ) +| |~з|2' 5 )| q 22)||2 ( 5 ) ) d5.
Оценим q 3 :
|~ 3 ( x )| < I f ! ( x )| ( 1 + r|B 2 q (2) I ) + Z ® J ( x ),
j = 1
где
^ 1 ( x ) = /| ( f ,(1) )( X )| B 2 q (1) — B 2 q (2)^ ^ 2 ( x ) = 2| B 4 q (1) — B 4 q(2)^ to 3( x ) = B 2 q (1)| y« 2 ( x ), to 4( x ) = 2| B 4 q (2)| B 2 q (1) — B 2 q(2)^ Во-первых, мы имеем
® 1 ( x ) < 2 1( f(1) )( x )| ( q 31) ||( x )||~ 2 1( x ) +1 1~ 3 1( x )| qq 22) ||( x )].
Во-вторых,
® 2 < x ) < 2 j|~ 3 ( 5 ) q'l ’ t&ix — 5 ) + q 32) ( 5 ) ~ 1 ( 5 .2 x ■ 5 ) d5
γ 0
< Y[|*1Кx
В-третьих,
x
x
x
® з ( x ) < B 2 q (1) y ^ 2 ( x ) < Yg)i ( x )f | q 31) ( 5 ) q 21) ( 5 )| d5 < Y^ 2
2 0 2
В-четвертых,
ω 4
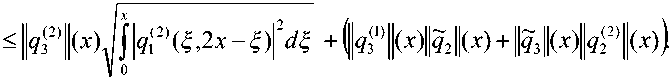
n 2 n
Принимая во внимание
2 Ы < n 2 k J2,
V i = 1 7 i = 1
получим ~ 32 ( x ) < 10 / ;2 ( x )(1 + Y2B 2 q <2)| )
+ 5y к к ( x )| 2 V q 3(1) ||2 1 1~ 2 Г ( x ) + I q 22) ||21 |~ 3 Г ( x ) 7
+ 20 ||~з||2(x)jq1(1)(5,2x-5)2d5 + |q(2)||2jq(2)(5,2x-5)2d5 x 1 + Y|q/flq21)! Y V о о 7 k 4
+ 1 01 q 3 2) Г j k2) ( 5 ,2 x - 5 ) 2 d5 ( l q 31) ГI^ ^ 2 Г ( x ) + 1 q 22) ||21 q . Г ( x ) ) .
Таким образом, имеем
II~3|2(x) + Yj|/5)|2(Iq/lq.l'f-) + |q!2)||2|q |'<5)7d5 + 221 j|q.| <5)J:-■ (-.2.-Z)|2dZd5 +1 q;2’||2||~1||2(I,x>)xf1+Y21q<"||2|q!"||2 Y k 00 2 k 4 + ‘0| q (2)|Г j (Iq 3'T fell2(5)+| q 22)||2| |~з|Г(5) 7+ j qjp*Z^25 - z )|2dZd5. Для удобства обозначим P1(x) = ||~1||2(l,x), Pj(x) = ||~j|P(x), j = 2,3 x G (0,1). Введем обозначения «= 10+5Y|q32)|||q22)|| , ^2 =| 1^2+5q3l)||2|qИ2 к32)ll2, k 2 7 kY 2 ^3(4) = 5Y21/■"'-)| qЗЦ2+10|q32)|p|q3'’||2jql2’(4,25 -Z)|2dZ, M,(Z) = 5Y21/.("(-I q22l||2 +[20+5q3"||2|q2"||27jqf"(4,25-Z)|2dZ 2 v y7 ξ +10 q32)||2 |q22l|| 2j qiP^ZIZ - ZfdZ,(18) Введем функцию P (x) = (5 + A + 5^2 )|/||2 +jx 2 к,(5)Р,(5) d5,(19) 0 j=1 Следовательно, [3] P'(x ) P(x) <]2 kxx), j=1 и, применяя неравенство Гронуолла, получим P(x) < P(x) < P(0) exp< J £ kj 5)d5 >. „ о j=1 С другой стороны, учитывая равенство x 5 , x (2x5' Л JJ ~Ц252§ — 5) d§d5 = - J J №, Z) dZ d5'= 2 ‘ 0 к 5' имеем ki< 5Mσ2 2σ*2 к 1+ —+ γ2 5lMσ2 γ2σ*2 exp < —°' 2°2 x24 Jk2(5)d5<|l + 5в|-г + 10el-f exp< 0 к 2 7 °* °* 2lM2 * x "Г (I +10 в )exp< γ2 Таким образом, получаем 2 ( I~|| = P(x) < 15 + x exp< 5zm ;( 2σ*2 к к 1' γ2 + -^-( l +10 в )exp< γ = 15 + к lM2' 2°*2 5lM2 —exp< 5lM2 H--- γ2σ*2 lM2' 2°*2 50M25lM ------H γ ** 251 к M, >+5le(1+Y2 )exp< —° 2°*2 exp< (15 25lM, >+ + lM кY 2) к 22 γ2σ*2 σ 2σ*2 7 A > + 51в 1 + — 1+ к ( l2 2lM2 2 * exp< 55l2βM2 +--F^°exp< γ2*2 —° 2°, A 3 A M^ ° * у 5lM2 2 *2 к 5 M2 J y о * у xexp< 3l + 5в +— ^+ — + к Y 7 °* к Y + (10 el-^ + 5 le + 70le к °* Y 7 Получим оценку для (1) 2lM2 2 * + (l + 5в) -° +10 в!-г exp< 2 * * 55l2βM2 +----3 3 exp < γ2 *2 exp< Y 7 ' lM. exp< 21-21 ° *2 ° 1) 2σ*2 5lM2 2 *2 2512M4 + 2γ2*4 1°^) Y 7 exp< lMσ2 2σ*2 exp< 2lM2 *2 55l2βM2 +----3 3 exp< γ2*2 5lM2 2 *2 — H1(0,l) . По лемме Гронуолла имеем II~ .<0,) < 3t(^,2'<+0))2+M 1 ~з|С,(0,) В итоге получаем II~'lII2(0,l) < 3[(°(2)(+0))2 + lM2 lexp< 21-21 ° *2 >C1||f — f<2)]2< C2||g(1) — g(2) 2H1(0.2l), (20) где C2 = з[с02 p0 +1-; ] exp< 2l-21 °.2 кl + YT J C1. Учитывая, что °(1)(+0) = °(2)(+0), получим L2(0,l) ||~‘||2 L2 (0,l) < lC1||g'" — g(2) 2 H1(0,2l) . Складывая оценки, получим <«,) ^ -^L,„, где C = C2 (l +1). Результаты и их обсуждение Теорема 1.5. Пусть для g(1) , g(2)из класса G(l, β,γ) существуют 7(1),7<2) е£(l,—7,c0,р0,7*) как решения обратной задачи (1)–(4) соответственно. Тогда 17"’—7<2,ii;.10, )^ Cg”) — где ( j) ( j) ( j) ( j) f = (f. , f2 , f3 ), (j) 1 (i) (i) f. (x. t)=2 (g )(t+x)—Ig )(t—x). f2 (j) =— 1. f,(j)(xx) = — 2(g‘j)) (2'x). j = 1.2. γ γ 2 l—7 1 50—7 х 15+^T7+ V Y 7 * 5lM 2 σ* 2 σ* σ 5 —7) γ2σ 25lI — * 7 im 7' 27*2 V 7 * Y ) 7* 2 —71 7 *2 25l2M4 24 2γσ 10 leI γ2 55l2βM σ2 γ 22 σ* exp < 5lMσ2 2σ*2 l—7' 27*2 . Заключение, выводы Для доказательства условной корректности рассматриваемой задачи, доказана теорема, где в отличие от аналогичной теоремы в [3] в вышеприведенной теореме при выводе требуемой константы в основном неравенстве использовалась не оценка вектора q, а оценки каждой из его компонент q1 ,q2,q3 . В работе [3] в выкладках норма каждой компоненты оценивалась через норму вектора q, так как оценка нормы вектора q есть сумма оценок его компонент. А в данной работе, как сказано, выше, уже использовались непосредственно оценки каждой компоненты.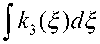
C = 3(l +1) l + -y [c0 P02+1—„■ ]expl
V
Y)
1+
V
exp<
( l2
х exp^ 3l + 5в + —--7 + — +
(V
(
+ 10 el—7 + 5le +
70е I
Y7
exp<
V Y
exp*
+
Список литературы Корректность обратной задачи акустики
- Кабанихин С. И., Искаков К. Т. Обратные и некорректные задачи для гиперболических уравнений. -Алматы: КазНПУ имени Абая, 2007. -330 с.
- Tyulepberdinova G. A., Nurseitova А. Т. The finite difference method of solving 1d inverse acoustic problem//Abstract of the 3d congress of the world mathematical society of the Turkic countries/al. Farabi KazNU. -Almaty, 2009. Vol. 2, № 6. -P. 66-67.
- Кабанихин С И., Бектемесов М. А., Нурсеитова А. Т. Итерационные методы решения обратных и некорректных задач с данными на части границы. -Алматы: Международный фонд обратных задач, 2006. -432 c.


