Космологические модели на основе асимметричного скалярного Хиггсова дублета с потенциальным взаимодействием между компонентами

Опишем базовые соотношения математической модели космологической эволюции классического скалярного Хиггсова поля основанной на асимметричном скалярном дублете и ее основные свойства. В качестве полевой модели рассмотрим самосогласованную систему уравнений Эйнштейна, классического Ф и фантомного ф скалярных полей, с потенциалом Хиггса [1], которому соответствует функция Лагранжа ^{1 2}

где

L=± (g lmi

- 2V&)) + + ( - g lmglgm - ^{2 v ( ф} )) + ±^{үф 2 ф 2} .

V (Ф)

α

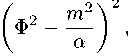
(ф)

v

β

φ

µ ²

β

– потенциальная энергия Хиггса соответствующих скалярных полей, α и β константы их самодей-ствия, γ - константа взаимодействия компонент дублета, m и µ – их массы квантов.

Канонический тензор энергии-импульса (см., например, [3]) скалярного дублета относительно функции Лагранжа (1) имеет вид

δ ^k                                 δ ^k

8nT ^k = Ф ,і Ф ， ^к -十 Ф ,j Ф ， ^j + 隙 V(Ф) - ф ,і ф ， ^к + 十 Ф ,j Ф ， ^j + 隙 v(ф) - 5 к үФ 2 ф².           ⑶

Гравитационное поле скалярного дублета описывается уравнениями Эйнштейна с тензором энергии-импульса T k (3) и затравочной космологической постоянной Л о

Затравочное значение космологической постоянной Л о связана с её наблюдаемым значением Л, получающимся при изъятии постоянного слагаемого в потенциальной энергии, соотношением

^Л = ^Л о

m ⁴

4a

µ ⁴

4e

.

Функции Лагранжа (1) соответствуют уравнения скалярных полей:

АФ + % - 2үФф ² = 0;

где

- Аф + v ； - 2үФ 2 ф = 0,

^△ =•

1. Полная система уравнений для метрики Фридмана

В случае пространственно-плоской метрики Фридмана

ds ² = dt ² - a ² (t)(dx ² + dy ² + dz ² )

-где a(t) - масштабный фактор и не зависящих от трехмерных координат скалярных полей Ф(t), ф(t) тензор энергии-импульса скалярного поля принимает изотропную структуру

T k = (е+Р* 4 6 4 - pS k ,

¹ 3десь и далее используется планковская система единиц G = h = c = 1 .

² The work is performed according to the Russian Government Program of Competitive Growth of Kazan Federal University.

где е = Т4 =    (1Ф2 + V(Ф)) +   (-132 + v(°)) — 二ҮФ2。2；(11)

8n 2               8n    28n p = —Ta = fl市2 - V(ф)) - f|32 + v(0)) + ^-үф202,(12)

8n у 2          у 8n у 2у 8n так что е + p =3®2 — 32),(13)

8n где ε - плотность энергии и p - давление космологической системы.

Уравнения полей скалярного дублета (6)–(7) в метрике (9) принимают вид

Ф + 3aФ + % - 2үФ32 = 0;(14)

a

• -3 - 3~3 + v； - 2үФ23 = 0.(15)

Нетрудно видеть,что из всех уравнений Эйнштейна (4) только два нетривиальных:

4 ：3   - хФ2 - V (Ф) + 5 32 - v(3) + үФ232 - Ло = 0(16)

a2   22

办 a2 i1

：2- + — + ^Ф2 - V(Ф)-三而2 - v(3) + үФ232 - Ло = 0(17)

a a2 22

Придадим этим уравнениям более компактный вид, переходя от независимой переменной a(t) к переменной H(t) (см. [4] и содержащиеся там комментарии). Для этого продифференцируем по времени уравнение Эйнштейна (16)

62a a ²

60 3 - ФФ - % Ф + 33-v ； Ф

• -2үФФ3 2 - 2үФ ² 而 3 = 0.

  
  

Умножая обе части уравнений поля (14) и (15) соответственно на Ф и 3 и подставляя результат в (16), получим

₃ a / 2a aa

W +Ф 2-j ² ) =0. a ²

Вводя далее параметр Хаббла

H

a

^, a

перепишем (19) в форме

/ • Ф2

^{6 HH+}т -

而 ²

0 今

H= -步 ² +2 。 ²

Заметим, что уравнение (21) можно записать в эквивалентном виде, складывая уравнения (16) и (17) и применяя подстановку (6)

H

т ² ф ²

-3H ² +

аФ ⁴    〃 ² 3 2

+

^в 3үФ ² 3 ² + л .

• 1.1.    Нормальная система динамических уравнений

Полученной системе уравнений можно придать нормальный вид, т.е., представить её в виде системы обыкновенных дифференциальных уравнений первого порядка разрешенных относительно производных:

Ф = Z,

Z = - 3HZ - m 2 Ф + аФ ³ + 2үФ0 2 , Ф = ^z,

Z = — 3Hz + 儿 ² ф — /Ф ³ — 2үФ 2 ф,

H

Z ²    z ²

- Т + У ■

Также с учетом (22) эту систему можно записать в следующем виде, удобным для качественного анализа:

Ф = Z,

Z = —3HZ — т2Ф + аФ3 + 2ү Фф2, ф = z, z = — 3Hz + 〃2Ф — вФ3 — 2үФ2ф,

• о т ² Ф ² аФ 4    〃 ² ф ² вф 4      ? ?

H = — 3H ² + -^---4- + 子—— Ү Ф ² ф ² + Л.

Таким образом, нормальная система динамических уравнений (28)–(32) описывает фазовые траектории в пятимерном фазовом арифметическом пространстве R 5 = { Ф, Z, ф, z, H } . Каждой конкретной фазовой траектории, определяемой начальными условиями, в этом фазовом пространстве соответствует конкретная космологическая модель. Можно показать, что уравнение (16) является первым интегралом динамической системы (28)–(32):

3H 2 — Z ² + 迎— - 2 1 2 + z ² + 纪—亞 + үФ 2 ф 2 — Л = 0. 2      4       2      2     4       2     ' 屮

Уравнение (33) определяет гиперповерхность в фазовом пространстве динамической системы (28)– (32), на которой лежат все фазовые траектории этой системы. В дальнейшем эту гиперповерхность будем называть гиперповерхностью Эйнштейна-Хиггса .

Уравнение (33) можно записать в форме

3H ² —E = 0,

где неотрицательная величина E - эффективная энергия системы :

E 三 I - F + -Ф ² - ф 2 -号 + У - үФ 2 ф 2 +Л >  0, 2     4       2      2     4      2

Отметим полезное соотношение для определения инвариантного космологического ускорения

„ aa H 1 ,       、

° = 02 三 1 + H2 = -2(1 + 3к), где к = - - эффективный коэффициент баротропы.

В работе проведен детальный качественный анализ динамической системы (28)–(32) и показано, что при

〃 ⁴ +4вЛ >  0

динамическая системы (28)–(32) имеет две и только две устойчивые (притягивающие) особые точки M + ± .

Кроме того, исследованы асимптотики решений системы (28)–(32) вблизи космологической сингулярностей и показано, что к состоянию сингулярности модель приближается со значением эффективного коэффициента баротропы к = 1, что соответствует предельному жесткому уравнению состояния.

• 1.2.    Модель с бесконечными прошлым и будущим с начальными условиями вблизи особой точки M ₀ ⁺ _,0 ; Λ = 0

В качестве примера рассмотрим модель с фундаментальными параметрами P и начальными условиями I (подробности см. в [5])

P 三 [[а,в,т, 〃 ], Л,ү]= 卩⑴ =[[1,1,1,1], 0, 5 • 10 ^{- 5} ];                 (37)

I 三 [@(0),Z(0), 0(0),z(0), H (0) = e • H o ]= I ⑴ =[10 ^{- 3} , 0,10 ^{- 5} ,0,1],                 (38)

где e = ± 1, H o — неотрицательный корень уравнения (33).

Данная модель относится к классу космологических моделей с бесконечными прошлым и будущим. На Рис. 1 показана эволюция геометрических факторов £(t) и H(t), а на Рис. 2 эволюция скалярных потенциалов для модели с параметрами Р ( 1 ) и начальными условиями I ( 1 ) . Как можно видно из графиков на Рис. 1, данная модель имеет инфляционные начало и конец, причем на начальном этапе происходит инфляционное сжатие с H 心一 0.289, которое сменяется инфляционным расширением на конечном этапе с H 心 +0.289. Указанные инфляционные этапы связаны “мостиком” с очень малым постоянным значением параметра Хаббла H 仁 4 • 10 ^{- 4} , £ т 0 今 a(t) 仁 1. Можно сказать, что на интервале t е [-15,15] Вселенная является почти Евклидовой. Поскольку полная энергия космологической системы E согласно (34) равна 3H ² , то на этом промежуточном этапе полная энергия стремится к нулю E 仁 10 ^{- 7} . Заметим, что предположение о существовании Евклидовых циклов было сформулировано в работе авторов [2].

При этом как раз на промежуточном этапе происходят сильные колебания потенциалов скалярных полей: потенциал классического поля Ф выходит из устойчивого состояния Ф = 0 и после нескольких колебаний возвращается в прежнее состояние. Потенциал фантомного поля ϕ переходит из устойчивого состояние ф = 1 в неустойчивое состояние ф = 0 и затем возвращается в прежнее состояние.

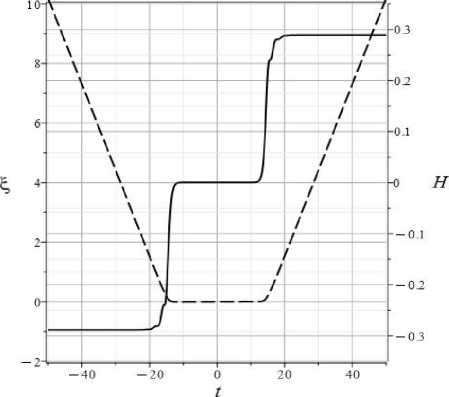
Рис. 1. £(t) — штриховая линия; H(t) 一 сплошная линия.

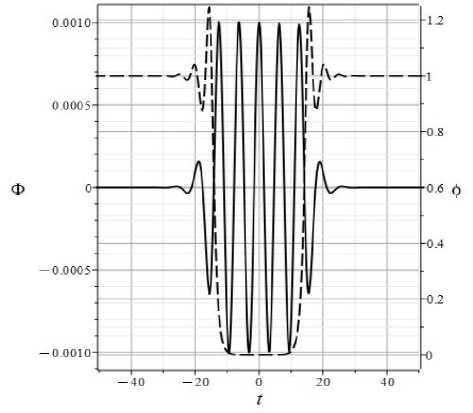
Рис. 2. Фазовая траектория модели Р ( 1 ) в плоскости

{ Ф , 。 } .

Заключение

• 1.    В зависимости от значений фундаментальных параметров космологические модели на основе асимметричного скалярного Хиггсова дублета возможен широкий спектр типов её поведения, среди которых модели с бесконечными инфляционными прошлым и будущим, модели с начальной сингулярностью и бесконечным инфляционным будущим, с бесконечным инфляционным прошлым и конечным будущим (Big Rip), с конечными прошлым и будущим.

• 2.    В частности при достаточно больших значениях константы взаимодействия γ ≳ 0.49 космологическая эволюция быстро заканчивается Big Rip’ом, что делает непригодными космологические модели на основе асимметричного скалярного Хиггсова дублета с большими значениями константы взаимодействия.

• 3.    В ряде случаев модели имеют точки отскока, в которых происходит процесс перехода из одного устойчивого состояния в другое.

• 4.    В ряде случаев модели допускают фазу почти Евклидова цикла, на котором Вселенная является почти Евклидовой за счет практически полной компенсации энергии полей дублета.