Крупномодульные опоры как средство повышения самостоятельности студентов при обучении математике

Согласно федеральному закону "О высшем и послевузовском профессиональном образовании" научно-педагогические работники высшего учебного заведения обязаны развивать у обучающихся самостоятельность1. В связи с чем в

• ¹    Федеральный закон "О высшем и послевузовском профессиональном образовании". URL: http://fgosvo.ru/uploadfiles/npo/20120330235028.pdf

высшей школе уменьшается количество аудиторных часов на изучение многих дисциплин, в частности математики, при этом увеличивается количество часов на самостоятельную работу студентов. В современной «педагогике совершенно четко обозначилась проблема несоответствия увеличивающегося объема информации количеству учебного времени» [1, с.13], соответственно возникла проблема усвоения студентами большего количества информации за малый временной промежуток. Но дидактическую проблему можно обосновать исторически, «по причине естественного бесконечного увеличения объема школьных знаний» [1, с.16], и она неиссякаема как космос. Решение указанных проблем заключается в самой дидактической задаче педагога – громоздкое сделать компактным, продолжительное – кратким, сложное и непонятное сделать простым и яcным. Считаем природосообразным то, что всю преподаваемую информацию педагог должен «пропустить» через себя, «обработать» и выдать ее для соответствующего контингента в соответствующих условиях. Здесь уместно привести слова Александра Александровича Зиновьева «Мудрость – это упрощение мысли, не некая примитивизация ее, а доведение результатов до такого состояния, когда эти мысли можно смело сообщать другим, даже стоящим на более низком уровне развития, не боясь, что не поймут» [2, с.7]. Описанное выше мы отнесли к высшей математике: как студентам, обучающихся на нематематическом факультете объяснить математику так, чтобы было наглядно, понятно, чтобы они не запутались в огромном количестве формул, графиков, понятий, как уплотнить математическую информацию.

Разрешение поставленных проблем находится в самом понятии самостоятельной учебной деятельности – целенаправленная деятельность, ориентированная на усвоение знаний и умений, выделив такие «приемы самостоятельной учебной деятельности, как: прием смысловой переработки текста, приемы краткой и рациональной записи материала, выделение в материале исходных, главных идей» [3, с.63]. А реализация таких указанных приемов возможна через крупномодульные образно-графические наглядности, получившие в дидактике название – крупномодульные опоры. Применение таких опор позволяет достигать целей преподавания математических дисциплин в вузе для студентов нематематических факультетов:

• -    знакомить студентов с основами математического аппарата, необходимого для решения как теоретических, так и практических задач различного профиля;

• -    повышать самостоятельность студентов при работе с учебной литературой по высшей математике;

• -    увеличить уровень математической культуры;

• -    развивать алгоритмическое и логическое мышление;

• -    формировать навыки математического исследования для решения прикладных задач и умения использовать математический язык для выполнения профессиональных задач.

Всем известно, что математику выучить на зубок невозможно, остается только ее понять. Еще П.М. Эрдниев утверждал, что вся математика состоит из контрастных - парных знаний и «ее необходимо преподавать крупными блоками» [4, с.169]. Например, воспользовавшись его идеями, совместно и одновременно знакомили студентов с законами распределения непрерывных случайных величин: показательный, равномерный, нормальный на одной лекции. Эти законы представлялись им сразу в виде одной таблицы, в которой отражены: функция распределения и ее график, плотность распределения и ее график, числовые характеристики, а также формулы для нахождения вероятностей попадания случайной величины в интервал. Хватало времени на этой же лекции доказывать теоремы и решать задачи. П.М. Эрдниев использовал в своей работе схемы, таблицы - приемы укрупненных дидактических единиц, которые позволяют познакомить единым взором с целой теорией и увидеть те ее детали, которые остаются в тени при словесном способе. Теория, представленная граф-схемой или блок-схемой обычно лучше понимается и быстрее запоминается как учениками, так и студентами. Например, студентов мы «учили решать задачи на практическом занятии “Законы распределения дискретных случайных величин” по математическому разделу ”Элементы теории вероятностей”» [5, с. 84] с помощью алгоритмической блок-схемы (рис.4), по которой легко было видеть особенности и отличия каждого закона, а также удобно использовать при решении задач. Считаем незаменимым использовать блок-схему при изучении комбинаторного анализа.

Многолетний опыт преподавания высшей математики в вузе, основываясь на вышесказанном, позволил нам выделить свыше 60 крупномодульных опор по таким разделам как алгебра, аналитическая геометрия, математический анализ, исследование операций, дискретная математика, теория вероятностей, математическая статистика и заключить их в учебно-методическое пособие «Высшая математика в схемах и таблицах» [6, с. 11-75] по следующим типам:

• -    граф-схемы: схемы «паучок» (рис.1), многоугольные граф-схемы (рис.2), кластеры;

• -    блок-схемы: алгоритмические (рис.3) и логические (рис.4);

• -    прямоугольные таблично-матричные модули: таблицы (Табл.1).

В каждой из опор использованы такие виды кодирования как рисунок, график, чертеж, круги Эйлера или такие укрупнения учебной информации как формула, краткая запись, символическая запись с использованием кванторов и логических знаков операций.

Охарактеризуем граф-схемы, блок-схемы, таблицы как основные виды крупномодульных опор и опишем методику обучения высшей математике с их использованием. Под понятием графа понимаем совокупность вершин или точек, кое-какие соединены ребрами или отрезками попарно. В настоящее время граф-схемы являются самыми распространенными схемно-знаковыми моделями представления знаний в методике обучения школьных дисциплин, понимая при этом под «точкой» в граф-схеме любое наглядное представление с заполненной информацией, соединенное линией с другим наглядным представлением. Мы выделили два основных вида граф-схем для использования в высшей математике: схема- паучок и многоугольная граф-схема.

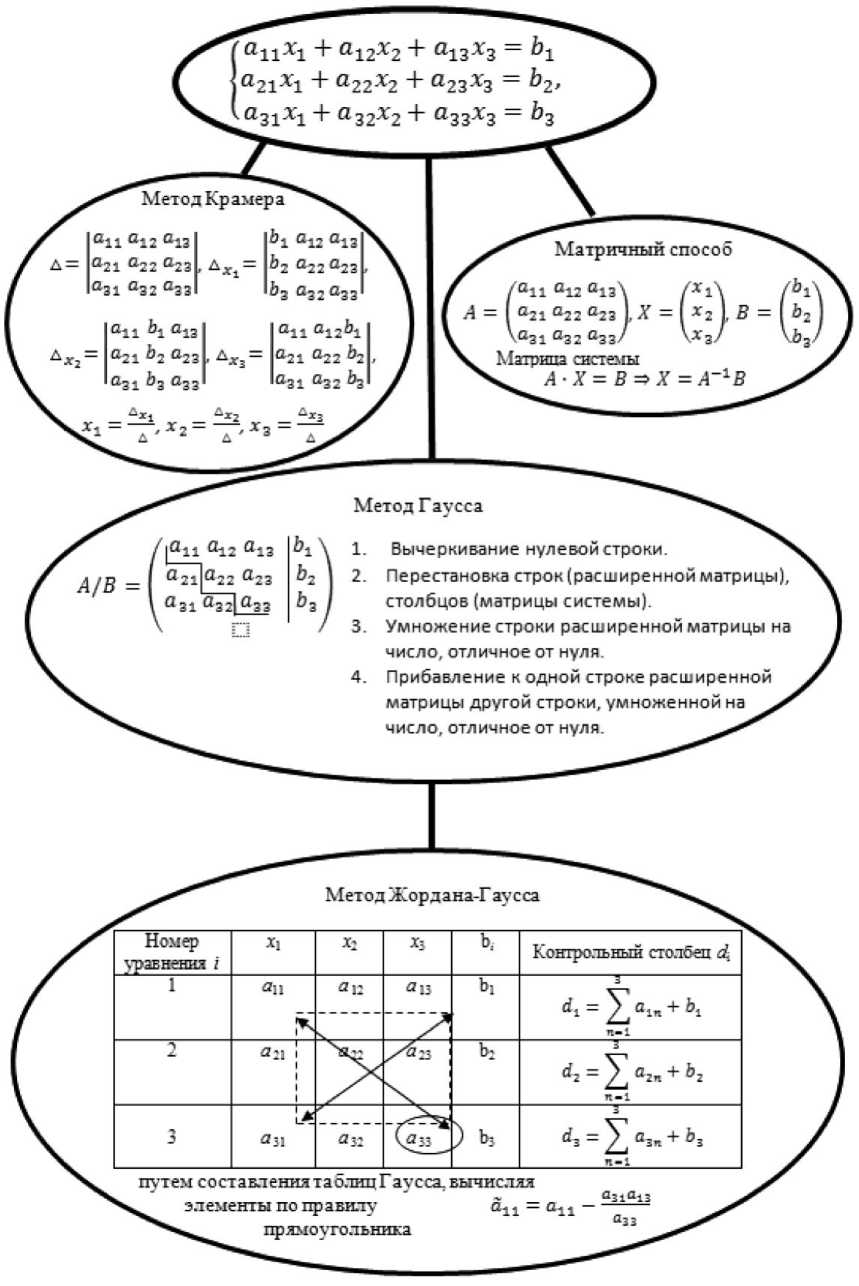
Рисунок 1. Схема-паучок «Способы решений систем линейных уравнений»

Figure 1. Scheme spider "Ways of Solutions of Systems of the Linear Equations"

Рассмотрим схему-паучок . Речь идет о граф-схемах типа «Паучок», в некоторых исследованиях такую граф-схему называют моно кластер - «это статическая

схема, на которой информация представляется в виде образа – паука» [7, с.36]. В центре схемы «туловища» - основное понятие, к «туловищу» с помощью линий присоединяются «ножки» - свойства рассматриваемого понятия или различные его определения, к «ножкам» присоединяются «башмачки» - это могут быть формулы, графики, а также следствия. На рисунке 1 представлена схема-паучок «Способы решений систем линейных уравнений». На этой схеме «туловищем» является общий вид системы линейных уравнений с тремя неизвестными, «ножками» являются способы решения этой системы: метод Крамера, матричный метод, метод Гаусса. Только одна ножка одета в «башмачок» - «Метод Жордана-Гаусса», так как он является модификацией метода Гаусса. Выше мы указали, что схему-паучок называют моно-кластером, а под кластерами понимаем такую схему, которая представляет большие объемы информации, в переводе с английского "cluster" означает рой, гроздь, груда, скопление. Элементами кластера, также как у схемы- паучка, являются овалы (туловище, ножки, башмачки) и линии (обозначающие связь между компонентами).

Рассмотрим многоугольную граф-схему . Под многоугольной граф-схемой мы понимаем способ моделирования логической структуры излагаемой математической информации, отличающийся от плана наглядными связями между элементами. На рисунке 2 представлена линейная граф-схема «Алгебраическая система высказываний». На схеме видно последовательность изложения информации: в начале говорится о том, что понимается под понятием высказывания (на схеме -I), далее вводятся определения логическим операциям над высказываниями с помощью таблицы истинности (на схеме – II), третьим шагом представлена информация о логических выражениях с переменными (на схеме – III) и на последнем шаге представлена самая важная информация – свойства операций над высказываниями, всего их 22 свойства (на схеме – IV). Но информация представлена для лучшего запоминания: 8 свойств операций связаны с конъюнкцией и 8 свойств – с дизъюнкцией, которые между собой обладают принципом двойственности: если в первом столбике свойств поменять конъюнкцию на дизъюнкцию, дизъюнкцию на конъюнкцию, ложность на истинность, истинность на ложность, то получим второй столбик свойств. Остальные 6 свойств выводятся или с первых восьми свойств или из второго пункта схемы – определений логических операций. Такую многоугольную граф-схему преподаватель изображает на одной доске, а на другой расписывает более подробно с примерами и доказательствами. Важно, чтобы граф-схема была представлена студентам в течение всего лекционного или практического занятия. Можно схемы представить также на электронной доске: заранее заготовленную или пользуясь инструментом «Перо» и функцией SMART Recorder, «с возможностью сохранения в видеофайл» [8, с.101].

Рассмотрим следующий вид крупномодульных опор – блок-схемы. Мы используем при обучении высшей математике логические и алгоритмический блок-схемы. Рассмотрим особенности алгоритмической блок-схемы. Под блок-схемами мы понимаем графическое изображение алгоритма решения определенных задач в виде схемы соединенных блоков (геометрических фигур) стрелками (линий перехода). Содержание блока – описание соответствующего действия.

I. Повествовательное предложение, о котором однозначно можно сказать истинно оно ложно

Высказывание^ А: «...»

________* истинное А=1 "'"-—* ложное А=0

П Логические операции: л, V, =>, <=>, отрицание
Название Обозначение чтение			Конъюнкция АлВ «А и В»	Дизъюнкция Av В «А или В»	Импликация А=> В «Если А, то В»		Экеиеатенция А<^В «Ат. ит.,к..-В»		А	Отрицание А «не А»
Определение			Истинна АлВ	Ложна Av В	Ложна А=> В		Истинна А$^В		1	0
А		В							0	1
0		0	0	0	1		1
0		1	0	1	1		0
1		8	0	1	0		0
1		1	1	1	1		1
Порядок выполнения операций: 1) отрицание: 2) «Л»; 3) «V»; «ф»; 4) < простого         равноправны высказывания Порядок нарушают только скобки								<=>»; 5) «<=> »
	Ш. Отношение « =»                               Выражения (F) (между выражениями с логическими         <___—-—'       —— переменными F)               Тождественно- Тождественно ни те, ни други истинные       ложные          F * 1, F = 1        7^=0        7^0
	IV. Основные равносильности (свойства операций)

1. А,^=ВлА	1°. AvB=BvA	Комм^латнвные
2. (АлЗ)лСзАа(ЗлС)	2е. (AvB)vC sAv(BvC)	Ассоциативные
3.	3°.(AaS)vC3(AvC)a(SvC)	Дн стрн бутнвные

(А V 3) л С = (А л С) v(3 л С)

4. А лВ г А V В	4°. AvB г А л В	Де Моргана
5. А,^4= А	5°. AvA=A	Склеивания
6. Ал Аг 0   Про тив ор ечия	6°. A v А г 1 Исключение третьего
7. АлОзО	7° Avl=l
8. Ал1=А	8°. AvOb А

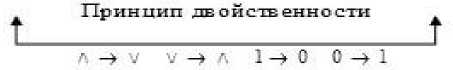
9. Аг А двойного отрицания                 70. А^В=А\/В

77. А -» 3 з (А => В) л(3 => А) = (.4 = В) з А © В = А © В

12. AVWB) =А\/В    13. AV(AAB') = А 14. Аф В = (A v В) л (Av В)

Рисунок 2. Многоугольная граф-схема «Алгебраическая система высказываний» Figure 2. Polygonal flowgraph "Algebraic system of statements"

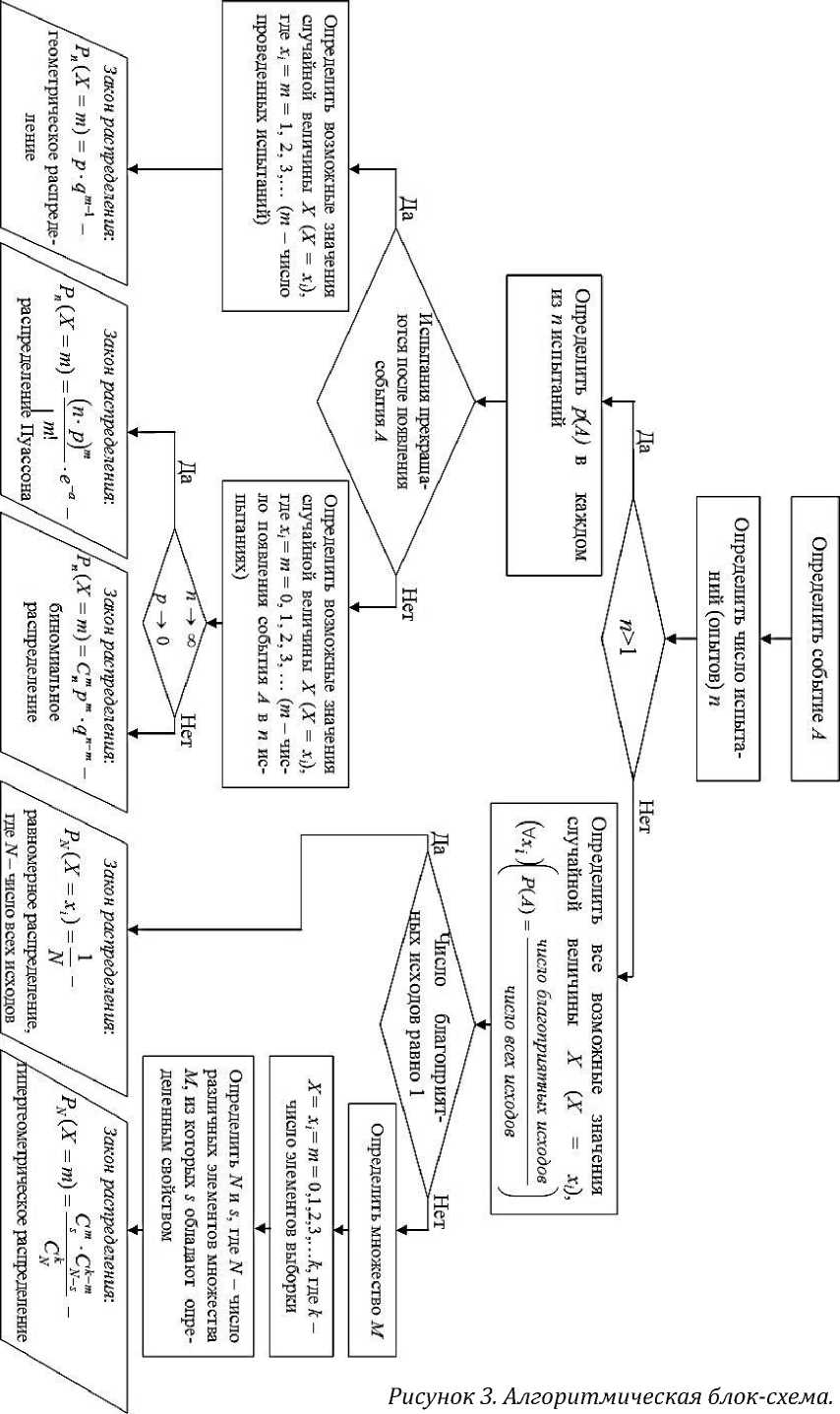
Figure 3. Algorithmic block diagram

Мы используем такие основные графические символы для изображения блок-схем алгоритмов как прямоугольник - блок для обозначения выполнения операции, ромб - блок для обозначения проверки условия, параллелограмм -блок вывода информации (в основном у нас это какая-то формула). На рисунке 3 представлена блок-схема «Закон распределения дискретных случайных величин», которая используется при решении вероятностных задач. В ней используются такие базовые структуры блок-схем алгоритмов как следование и ветвление.

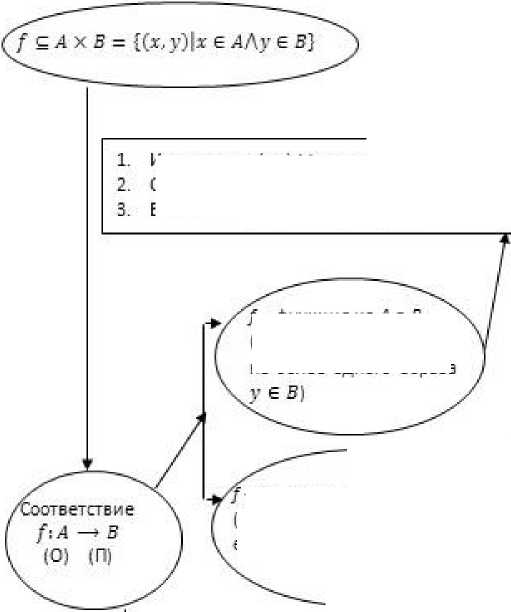
Рассмотрим особенности логической блок-схемы, используя наиболее устоявшийся подход в дидактике «на блок-схеме учебный материал может располагаться в виде трех порций: основание теории, ядро теории и приложения теории» [9, c.76]. На рисунке 4 представлена логическая блок-схема, состоящая из трех порций: основание теории - понятия декартова произведения множеств и соответствия; ядро теории - такие понятия как бинарное отношение, функция и отображение (они рассматриваются параллельно); приложение теории - используемые свойства функции и отображения при решении задач, а также используемые виды бинарных отношение при решении задач. Отметим, что каждая порция – символическая запись с использованием кванторов и логических знаков операций.

Рассмотрим особенности прямоугольных таблично-матричных модулей. Мы выделили только один тип таких модулей при обучении высшей математике – таблица, что в переводе с латинского языка tabula - доска. В настоящее время самая известная таблица - таблица химических элементов Д.И. Менделеева, в математике самая известная таблица - таблица умножения. По аналогии и мы использовали при обучении высшей математике таблицы как множество цифровых и текстовых данных с использованием формул, рисунков и графиков, расположенных в определенном порядке по строкам и столбцам. Приведен пример таблицы -составление уравнения плоскости (Табл.1). По таблицы видно, что уравнение плоскости можно составить несколькими способами: 1) по координатам точки, лежащей в плоскости и координатам перпендикулярного вектора к плоскости (строка №1), 2) через координаты трех точек, лежащих в плоскости (строка №2); 3) через точки, в которых плоскость пересекает оси координат (строка №3).

Охарактеризуем методику использования крупномодульных опор при изучении высшей математики. Такого вида схемо-знаковых моделей как крупномодульные опоры обязательно использовать как на лекционных та и на практических занятиях. Лекционные занятия с использованием опор выстраиваются от целого к части. Вначале преподаватель дает представление обо всей изучаемой теме - знакомит студентов с соответствующей опорой: она может быть представлена в распечатанном виде (все зависит от аудиторного времени), на электронной доске или преподаватель фиксирует ее на обычной доске, как было сказано выше. После ознакомления с опорой студентам предлагается план лекционного занятия. В каждом пункте плана преподаватель раскрывает структурные составляющие опоры и приводит конкретные примеры. Проведение лекционного занятия с применением крупномодульных опор можно сравнить с пазлами, из которых составляется картинка. Если брать каждый пазл в отдельности и рассматривать его подробно, то целостное восприятие картинки может и не сложится. А если в начале показать картинку, то по ней легко составить картинку из пазл. Такой методический прием заставляет студентов слушать и понимать учебную математическую информацию, а не зазубривать математическую теорию.

-отображение из А в В (каждый х Е А имеет единственный образ у Е В)

Инъективна (но)Е-экаждый у 6 В имеет не более одного прообраза х 6 А Сюрьективна (но) «-^каждый у Е В имеет не менее одного прообраза х Е А Биективна (но)Е-жаждый у Е В имеет единственный прообраз х Е А

.Г- функция из А в 5 (каждый х Е А имеет не более одного образа

Линейного порядка:

4,т — связно

—» (VX,y)(rryVl,TX)

Отношение эквивалентности:

• 1 .т — рефлексивно <—* (Vx)xrx)

• 2 .т — симметрично *-» (vx,y)(xry -»утх)

• З .т — транзитивно *—г (Vx,y,х)(хту л утх -» хтх)

  т - бинарное отношение на множестве А, если А = В

  
  

Отношение строго порядка:

т — антирефлекси ено t-* (vx)(xrx) т — антисимметрично *—*

(VX. у)(хту л х * у -* утх)

т — транзитивно th (Vx,y, х)(хту л утх -* хтх)

Отношение нестрого порядка:

• 1.    т — рефлексивно «—» (Vx)(xrx)

• 2.    т — антисимметрично

• 3.    т — транзитивно — (Vx,y, х)(хту л утх -* хтх)

— (Vx,у)(хту Ах * у-* утх)

Рисунок 4. Логическая блок-схема «Соответствия»

Figure 4. Logical flowchart "Compliances"

На лекционных занятиях при наращивании учебного материала преподаватель возвращается к опоре, неоднократно ее повторяя, и в течение лекционного занятия на доске появляется та самая опора, с которой студенты знакомились в начале лекции. Лекцию преподаватель заканчивает повторением структурных составляющих крупномодульной опоры. Поэтому важно не стирать ее в течение всей пары. Студенты при подготовке к следующей лекции могут за 15 минут повторить лекционный материал, пробежав глазами опоры. На следующей лекции преподаватель напоминает студентам об изученной на прошлой лекции опоре, используя средства электронной доски. На электронной доске на представленной опоре преподаватель делает соответствующие пометки с использованием ответов студентов, на что не должно уходить не более 10 минут. Если прошлая крупномодульная опора связана с новой лекцией, то преподаватель об этом говорит и предлагает новую порцию учебного материала. Отметим, что алгоритмические блок-схемы имеют свои методические особенности их использования на занятиях. На лекционных занятиях преподаватель вначале обращает внимание студентов на окончательный результат блок-схемы, затем показывает различие между результатами и пути следования к ним. В течение лекции идет объяснение решений задач строго по алгоритму, представленному с помощью блок-схемы. Подводя итог лекции, преподаватель уже читает блок-схему по направленным линиям. Эффективность опоры тем выше, чем больше понятий, определений или свойств можно раскрыть на основе представленных объектов. Крупномодульная опора является своего рода тренировочным материалом для студентов, так как в ней используется математическая терминология, например, символьные определения с использованием аппарата математической логики, в связи с чем усиливается смысловая нагрузка.

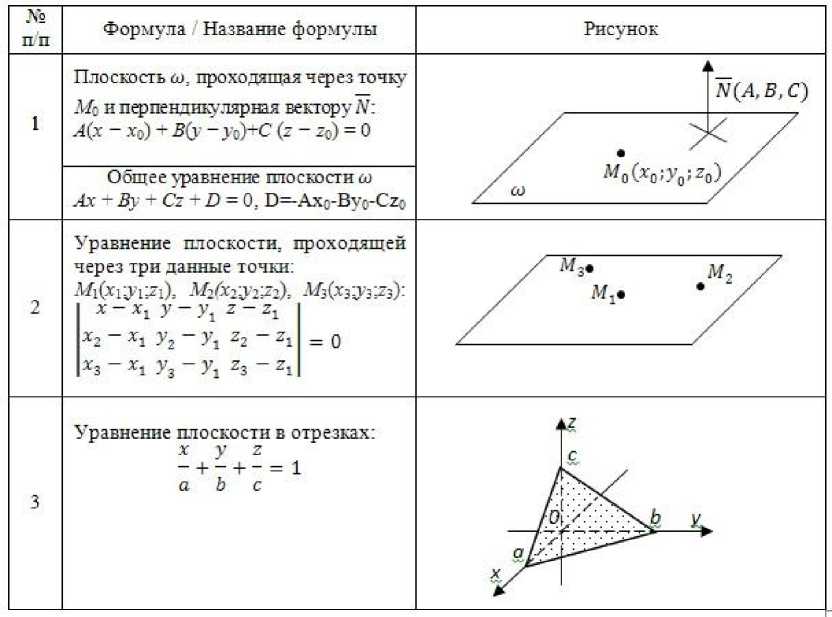
Таблица 1. Составление уравнения плоскости

Table 1. Drawing up equation of the plane

Использование крупномодульных опор на практических занятиях значительно расширяют их возможности. Каждое практическое занятие начинается с письменного воспроизведения опоры в течение заданного, заранее оговоренного времени на отметку. Студенты решают задачи, используя каждую структурную составляющую опоры. Неоценимую роль имеют опоры для подготовки к коллоквиуму, а также для успешной сдачи экзамена и зачета. Так как крупномодульные опоры - это краткое содержание теоретического материала в виде схем и таблиц, то преподаватель задает студентам на дом прочитать несколько раз не лекции, а схемы и таблицы по соответствующей лекции. Крупномодульные опоры облегчают нагрузку как преподавателя, так и студента, стало хватать времени на всю запланированную информацию. Нами было проведено анкетирование у студентов, обучающихся на экономическом, географическом, социологическом (ФИСМО) профилях первого и второго года обучения. Им задавалось семь вопросов с вариантами ответов, в вопросах слова «крупномодудьные опоры» заменялись на «опорные схемы»: 1.Как часто вы обращаетесь к опорным схемам? (никогда, редко, иногда, часто, достаточно часто). 2. Чем пользуетесь при решении задач из типовых расчетов и домашних заданий? (опорные схемы, лекционный материал, учебники, практический материал (конспекты практик), он-лайн калькуляторы). 3. Чем чаще всего вы пользуетесь при решении практических задач? (опорные схемы, лекционный материал, учебники, практический материал (конспекты практик), он-лайн калькуляторы). 4.Чем чаще всего вы пользуетесь при подготовке к зачету или экзамену? (опорные схемы, лекционный материал, учебники, практический материал (конспекты практик), интернет). 5. Помогают ли вам опорные схемы на практических занятиях? (да-нет- иногда). 6. Становится ли лекционный материал более понятным с использованием опорных схем? (очень-да-нет-иногда). 7. Укажите свое личное мнение об использовании опорных схем при обучении высшей математике. Почти 80 процентов ответов было за использование крупномодульных опор, более того, многие называли опорные схемы – «золотыми находками», некоторые утверждали, что если бы такое было в школе, то они знали бы математику лучше. И самое главное то, что большинство утверждало, что могут самостоятельно готовится к практическим занятиям, решать типовые расчеты с осмыслением, лекции уже не становятся тягостными, а даже интересными.

Таким образом, использование крупномодульных опор способствует развитию самостоятельности студентов и повышает их интерес к различным разделам высшей математики.