Математическая модель и программная реализация вычисления наибольшего интереса аудитории к медиа-проекту

Предположим, что отдельные передачи составляют медиа-проект или программу СМИ. В работах [1–3] приведены математические модели, позволяющие строить эффективный план выпуска передач длительных медиа-проектов в эфир с учетом неумень-шающегося интереса к передачам.

Настоящая статья посвящена математическим моделям эмоционального восприятия аудиторией передач и, как следствие, построению плана выпуска в эфир медиапроектов, основной целью которого является получение наибольшего интереса у аудитории для эффективного формирования общественного сознания [4].

Математические модели воспитания и интереса

Пусть n – количество полных воспитательных циклов [3] трансляции передачи, m_n – количество непрерывных трансляций пере-

дачи в воспитательном цикле с номером n , k_n – количество пропущенных трансляций в этом же воспитательном цикле, θ_n – коэффициент памяти зрителя или радиослушателя в полном воспитательном цикле с номером n , q_n – элементарное воспитание (эмоциональное воздействие) у зрителя в результате ознакомления с передачей в полном воспитательном цикле с номером n .

Согласно работам [1, 2], обобщая формулу воспитания W_{m , k} , полученного в результате непрерывных трансляций m_n передач [5] в полном воспитательном цикле n , можем записать соотношения:

mn wm к = qn-----+CF к , mn , kn-1      П П 1   0 П     mn-1 ,kn-1

где

F m ₁ , k ₁

m 1

= q^^

, (1)

F mn-1, kn-1

k n - 1

⁰ n - 1

q_n - 1

1 - "

1 - ¹¹-1

F_m „ = 0 .

m ₀ . n ₀

На основании формул (1) и работы [3] можно предложить равенство, описывающее интерес A n зрительской аудитории к передаче медиа-проекта, которое имеет вид

1 -em max Wm = q max-----+ 0 FmmX (7)

m                                  m , - 1

ⁿ , ^m            n , m 1 - 0

при условии

D = mnC <  A .         (8)

A

m

0 k (1 - 0 n ) q_n LJ- 5 ,

+ ^mFm k тп _j, кп _j

n

qnem-1 + 0m"  (0 -1)Fm  k л fl fl                  fl         n fl a mln-| ,kf

. (2)

Математическая формулировка оптимизационных задач

Пусть C_i – стоимость производства и трансляции одной передачи в эфире в полном

С учетом равенств (2) и (3) можно сформулировать другую оптимизационную задачу: "Найти количество полных воспитательных циклов, количество непрерывных трансляций передачи и количество пропущенных трансляций в каждом воспитательном цикле, обеспечивающих наибольший интерес аудитории к концу проекта".

Эта задача соответствует формуле: найти

воспитательном цикле i , i = 1, n , A - выделяемые средства на весь медиа-проект.

Тогда стоимость D производства и трансляции всех передач медиа-проекта будет удовлетворять соотношению

n

D = X m , C , .           (3)

i = 1

max  An = n,m1 ,k1 ,...,mn ,kn

= max n,m1 ,k1 ,...,mn ,kn

0 k (1 - O n ) f q, V

m n

1  θn      mn n 1 - 0 n    mn-1 •k'

^: n - 1

m q _n θ _n

- 1

+ 0m"

’ ( ⁰ n - 1) F m . - . , k ,

(9) при выполнении условия (5).

С учетом равенств (1) и (3) можно сформулировать следующую оптимизационную задачу: "Найти количество полных воспитательных циклов, количество непрерывных трансляций передачи и количество пропущенных трансляций в каждом воспитательном цикле, обеспечивающих наибольшее

При справедливости равенств (6) задача (9), (5) примет вид:

найти

max An = n,m

воспитание аудитории при завершении проекта". Последняя фраза математически описывается следующим образом:

найти

= max n , m

m

0 ^m - 1 (1 - 0 ) Я -T 0 + 0 m F m , m - 1 V 1 - 0

0 ^{- 1} + 0 ^{m - 1}( 0 - 1) F m , m - 1

. (10)

max n,m1 ,k1 ,..., mn ,kn

W mn ,kn-1

= max   qn n,m1,k1 ,...,mn,kn

1 - 0 m

1 - e n

+ em"Fm  k n      mn-1 , kn-1

при условии

n

D = X m , C , < A .        (5)

i = 1

Отметим, что при справедливости соот-

ношений

m j = m ,   k j = k = m - 1,

_     (6)

q j = q ,   0_} = 0 ,   С_з = C ,   j = 1, n

задача (4), (5) примет вид: найти

при условии (8).

Отметим, что задачи (4), (5); (9), (5); (7), (8); (10), (8) не учитывают продолжительность каждой передачи в полных воспитательных циклах.

Пусть T – время эфира, отведенное на трансляцию программы в эфире. Тогда, исходя из постановки задач (7), (8) и (10), (8) при условии равенства продолжительности t каждой из передач, верно соотношение

T t =---- .

nm

В этом случае можно величину C принять в качестве денежной суммы, определяющей стоимость передачи, длящейся единицу времени.

Исходя из этого допущения, условие (8) трансформируется в неравенство:

D = mnCt <  A .         (11)

Программные приложения для решения оптимизационных задач

Для решения задачи (7), (8) и (10), (11) были разработаны программные приложения. Программы написаны на языке программирования Delphi 7, выполняются под управлением ОС не ниже Wndows XP. Объемы загрузочных модулей каждой из программ не превышают 400 Кб. Для работы программ можно использовать компьютеры небольшой вычислительной мощности.

На программное приложение решения задачи (7), (8) было получено свидетельство о государственной регистрации [5], поэтому на описании его работы останавливаться не будем. На рисунке приведена главная форма программы решения оптимизационной задачи (10), (11). Программа позволяет строить план выпуска передач в эфир, обеспечивающий наибольший эмоциональный интерес аудитории при завершении программы. Программа также вычисляет необходимые финансовые затраты на производство передач медиа-проекта, значение воспитания, полученного в результате ознакомления аудитории с проектом, и необходимое количество полных воспитательных циклов программы.

Входные параметры программы легко прослеживаются на рисунке. Коэффициент памяти зрителя можно определить благодаря методике, предложенной в работах [3, 6].

Алгоритм работы программы основан на методе простого последовательного перебора с единичным шагом значений параметра m .

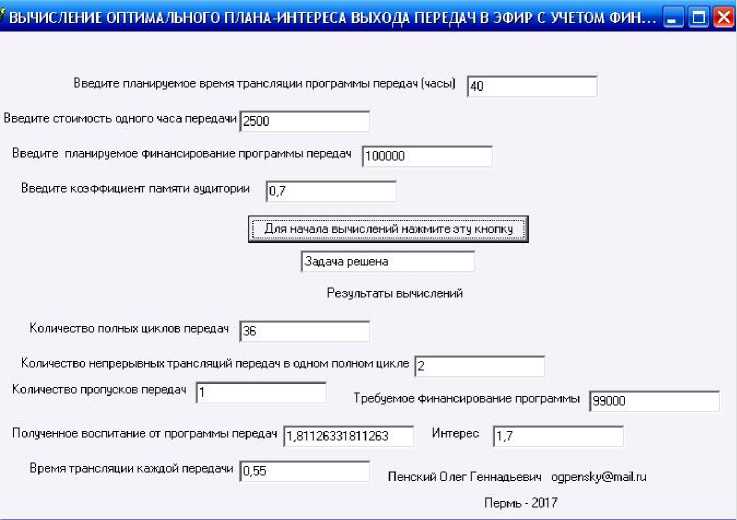
Главная форма программы

Вычислительные эксперименты

В таблице приведены результаты чис- нии оптимизационной задачи (10), (11) с по-ленных экспериментов, основанные на реше- мощью вышеописанной программы.

Результаты вычислительных экспериментов

θ	C 10 - 3 , руб/ч	A 10 - 3 , руб	T , час	m	k	n	D 10 - 3 , руб	Δ n	t , час
0,7	5,0	300,0	60	2	1	37	296,0	1,7	0,80
0,9	–	–	–	2	1	120	300,0	1,9	0,25
0,7	–	–	50	2	1	38	247,.0	1,7	0,65
0,9	–	–	–	2	1	125	250,0	1,9	0,20
0,7	3,0	–	60	2	1	37	177,6	1,7	0,80
0,9	–	–	–	2	1	120	180,0	1,9	0,25

Анализ таблицы позволяет утверждать, что в рамках поставленной оптимизационной задачи (10), (11) и заданных входных параметрах для расчетов: коэффициента памяти θ , стоимости C часа подготовки и транслирования передачи в эфире, выделяемых средств A на весь медиа-проект, планируемого времени T на всю трансляцию программы – аудитории с меньшим коэффициентом памяти θ соответствует меньший интерес Δ _n к медиа-проекту; необходимое количество непрерывных трансляций передач m и их пропусков k , обеспечивающих наибольший интерес Δ _n к проекту в конце проекта, остается постоянным при изменениях входных параметров модели; оптимальная длительность t каждой передачи проекта при уменьшении коэффициента памяти θ аудитории увеличивается.

Заключение

Таким образом, в статье впервые поставлены и описаны оптимизационные задачи, позволяющие формировать план выхода в эфир медиа-проектов с целью обеспечения наибольшего интереса аудитории к программам СМИ при ограниченных финансовых затратах.